1.Матрицы и действия над ними.

Таблица чисел вида , состоящая из _n строк и _m столбцов наз-тся матрицей размерности _n*m.

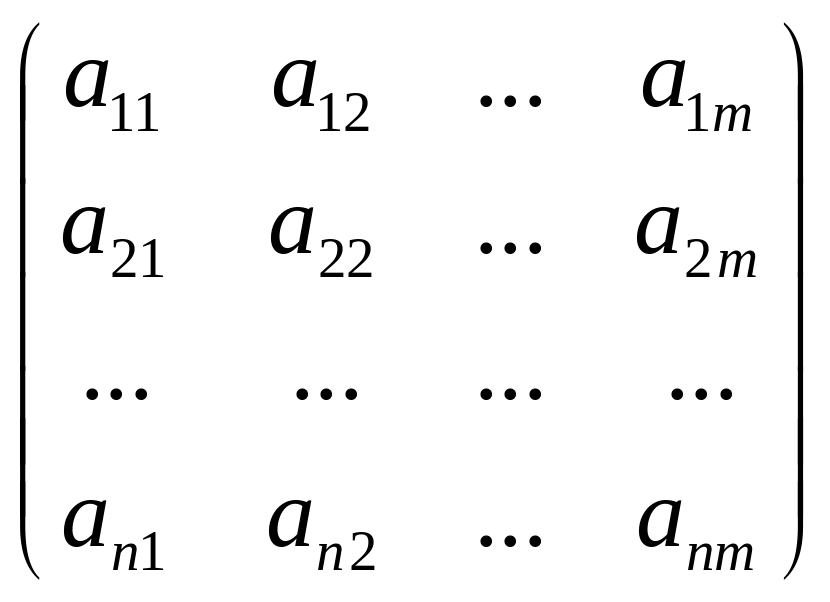
Числа наз-ют её элементами, если  , то матрицу наз-ют прямоугольной, если = ,то квадратной. Если =1, а 1,то матрица примет вид и наз-тся матрицей-строкой. Если же 1, а =1, то матрица наз-тся матрицей-столбцом. Число строк в кв.матрице наз-ют ее порядком. Две матрицы наз-ют равными если они имеют одинак. размерность и соответствующие элементы равны.

Сложение и вычитание матриц.Суммой двух матриц А и В одинакового размера  наз-тся матрица С размерности  ,эл-ты к-рой равны сумме соотв-щих элементов матриц А и В. Матрица 0 размерности  ,все эл-ты к-рой=0 наз-тся нулевой матрицей. .Разностью двух матриц А и В размерности  наз-тся матрица С размерности  такая, что А=В+С. Из определения следует,что эл-ты матрицы С равны разности соотв.эл-=ов матриц А и В.

Св-ва сложения: сложение матриц коммутативно, т.е. А+В=В+А, сложение матриц ассоциативно, т.е. (А+В)+С=А+(В+С), А+0=0+А=А

Умножение матриц на число. Произведение матрицы А на число  наз-тся матрицей 2А, элементы к-рой равны произведению числа  на соотв. элемент матрицы А.

Умножение матриц. Произведение матриц размерности  и матрицы В размерности наз-ся матрица С размерности , эл-ты к-рой вычисляются как сумма произведений соотв-щих эл-ов -строки матрицы А на -столбца матрицы В.

Пр.

Квадратная матрица порядка наз-тся единичной. Обозначается это матрица с единицами на главной диагонали.

Св-ва умножения: умножение не коммутативно, т.е. А*ВВ*А, умножение матриц ассоциативно, т.е. (А*В)*С=А*(В*С), если такие произведения существуют, если А матрицы размерности  , В размерности , то

_{Св-ва общие для операций над матрицами и операциями над числами: 1)А+В=В+А,2)(А+В)+С=А(В+С), 3)Т(А+В)=ТА+ТА (Т-число),4)А(В+С)=АВ+АС, 5)(А+В)С =АС+ВС,6)Т(А*В)=(ТА)В=А(ТВ),7)(АВ)С=А(ВС)}

_{Отличие операций над матрицами и над числами: а)если произведение матриц А В сущ-т, то произведение В на А м.не сущ-ть (А2*3, В3*3, В*А-нельзя, несогласованная матрица), б) если произвед.матриц АВ и ВА сущ.,то они м.б.матрицами разных размеров}

в)даже в случае когда оба произвед.А на В, В на А и им. одинак.размер,то переместительный (комутативный) для умножения в общем случае не выполняется

г)произв.2ух ненулевых матриц б.=0

возведение в степень. Целой полож.степенью ,где m>1 в кв.матрице А наз-т произведение А*А m раз. =Е, =А, * = ,( =

Транспонирование матрицы.Если в матрице А размерности  все стороки заменить соотв-щими столбцами, то получим матрицу размерности  , к-рую наз-ют транспонированной матрицей А.

Св-ва транспонирования: _, ,

Элементарные преобразования строк матрицы: умножение строк матрицы на ненулевое действительное число;прибавление к одной строке матрицы другой, умноженной на нек-рое число, с помощью элементарных преобразований можно поменять местами две любые строки матрицы.

Ступенчатая матрица-матрица, обладающая след. св-вами:1)если тая строка нулевая то также нулевая.2)если первые ненулевые эл-ты той строки и находятся соотв-но в столбцах с номерами и . Тогда 

Т. Любую матрицу можно привести к ступенчатому виду с помощью элементарных преобразований строк матрицы.

2.Определители, их св-ва. Определителем 2-го порядка наз-тся число, вычисляемое по ф-ле

Определителем -го порядка, соотв-щим квадратной матрице -го порядка, наз-тся число, равное сумме произведений эл-ов какой-либо строки(столбца) на их алгебраическое дополнение.

Минором наз-ют определитель, полученный из данного путем вычеркивания той строки и –того столбца.

Алгебраическим даполнением наз-ют число равное

Т.Лапласа:Определитель -го порядка равен произведению элементов какой-либо строки(столбца) на соотв-щее алгебраическое дополнение.

Пр.

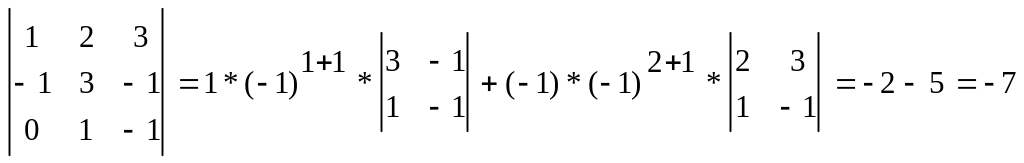
Св-ва определителя: 1)Определитель треугольной матрицы(все эл-ты матрицы расположенные ниже(выше) гл.диагонали=0) равен произведению эл-ов главной диагонали, 2)Опред. матрицы с нулевой строкой или нулевым столбцом равен нулю, 3)При транспонировании матрицы, определитель не меняется., 4)Если матрица А получается из матрицы В умножением каждого элемента нек-рой строки(столбца) на число ,то определитель равен , 5)Если матрица В получается из матрицы А перестановкой строк(столбцов), то определитель меняет знак.

6)Опред.матрицы с пропорциональными строками(столбцами) равен 0. 7)Опред. матрицы не меняется если к одной из строк прибавить другую, умноженную на нек-рое действительное число,8)Опред.произведения=произведению определителей.

, где А и В- квадратные матрицы одного порядка.