15. Упорядоченные и неупорядоченные разбиения множеств. Число Стирлинга 2-го рода. Формула и рекуррентное соотношение для числа Стирлинга 2-го рода.

 число Стирлинга второго рода   представляет собой количество неупорядоченных разбиений n-элементного множества на m частей, в то время какмультиномиальный коэффициент   выражает количество упорядоченных разбиений n-элементного множества на m частей фиксированного размера  . Количество всех неупорядоченных разбиений n-элементного множества задается числом Белла  .

Числом Стирлинга второго рода из n по k, обозначаемым   или  , называется количество неупорядоченных разбиений n-элементного множества на kнепустых подмножеств.

Числа Стирлинга второго рода удовлетворяют рекуррентному соотношению:

, для n ≥ 0,

, для n > 0,

 для 

---------------------------------------------------------------------------------------------------------------------------------------

16. Число Белла. Рекуррентное соотношение для числа Белла.

числом Белла   называется число всех неупорядоченных разбиений n-элементного множества, при этом по определению полагают  .

Числа Белла можно задать в рекуррентном виде:

.

---------------------------------------------------------------------------------------------------------------------------------------

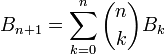17. Упорядоченные и неупорядоченные разбиения чисел. Рекуррентные соотношения для количества неупорядоченных разбиений натурального числа на фиксированное число слагаемых.

Разбие́ние числа́ n — это представление n в виде суммы положительных целых чисел, называемых частями. При этом порядок следования частей не учитывается (в отличие откомпозиций), то есть разбиения, отличающиеся только порядком частей, считаются равными. В канонической записи разбиения части перечисляются в невозрастающем порядке.

Количество разбиений числа n на слагаемые, используя числа не превышающие k:

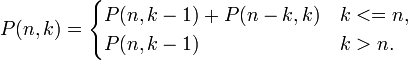
Количество разбиений натурального числа n на k слагаемых:

---------------------------------------------------------------------------------------------------------------------------------------

18. Система различных представителей. Теорема Холла (без доказательства).

Система различных представителей для семейтсва конечных множеств S = {A₁, A₂,..,A_i,…,A_m} есть система попарно различных элементов {a₁, a₂,…, a_i,…, a_m}, для которых a_i ∈ A_i [i=1,2…m].

Теорема Холла:

Пусть задано мн-во S, задан набор (необязательно различных) подмн-в из S T=( ). Тогда для Т сущ-т система различных представителей такая, что и подмн-ва { } [m] вып-тся условие : | | k

19. Система общих представителей, критерий существования.

Критерий существования:

пусть на множестве S задано семейство   из |I| = пэлементов, пконечно; для существования Р. п. с. необходимо и достаточно, чтобы  для каждого k-подмножества   и каждого k, k= =1, 2, . . ., п.

---------------------------------------------------------------------------------------------------------------------------------------

20. Теорема Рамсея.

Пусть  ,   и   — натуральные числа, причем  . Тогда существует число  , обладающее следующим свойством: если все  -элементные подмножества  -элементного множества   произвольным образом разбиты на два непересекающихся семейства   и  , то либо существует  -элементное подмножество множества  , все  -элементные подмножества которого содержатся в  , либо существует  -элементное подмножество, все  -элементные подмножества которого содержатся в  .

---------------------------------------------------------------------------------------------------------------------------------------

21. Булевы функции. Способы их задания. Число бул. Ф-ий от n переменных.

Логической ( булевой) функцией (или просто функцией) n переменных y = f(x₁, x₂, …, x_n) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.

Кол-во бул.ф-ий 2^(2^n)

22. Основные логические равносильности.

---------------------------------------------------------------------------------------------------------------------------------------

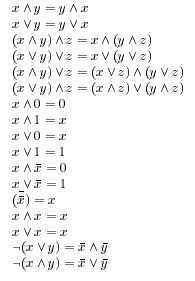
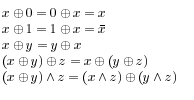
23. Разложение Шеннона и следствие из него.

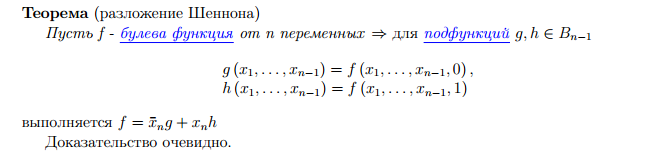
24. Двойственное разложение Шеннона и следствие из него.

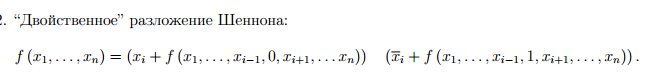
25.Дизъюнктивная нормальная форма (ДНФ) и конъюнктивная нормальная форма (КНФ). Совершенные ДНФ и КНФ.

Дизъюнктивной нормальной формой или ДНФ называется дизъюнкция простых конъюнкций. Например    — является ДНФ.

Совершенной дизъюнктивной нормальной формой или СДНФ  называется такая ДНФ, у которой в каждую конъюнкцию входят все переменные данного набора пременных, причём в одном и том же порядке. Например:  .

Конъюнктивная нормальная форма.КНФ — это конъюнкция простых дизъюнкций.

Совершенной конъюнктивной нормальной формой (СКНФ), называется такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного набора, причём в одном и том же порядке.

КНФ может быть преобразована к эквивалентной ей ДНФ путём раскрытия скобок по правилу: