Ортогональные планы второго порядка.
«+» ортогональных планов: малый объем вычислений; можно показать, что в матрице центрального композиционного плана не все столбцы ортогональны.
Для ортогональности матрицы необходимо преобразовать ее столбцы.
Значение звездного плеча α для различного числа факторов:
Число независимых переменных |
«Ядро» плана |
Число дополнительных опытов |
Величина α |
2 |
22 |
5 |
1 |
4 |
23 |
7 |
1,215 |
5 |
24 |
9 |
1,414 |
6 |
25-1 |
11 |
1,547 |
При α=1 новые переменные x1`и x2`:
x1`= x12-2/3;
x2`=x22 -2/3.
Матрицы ортогонального центрального композиционного плана 2го порядка 2х факторов.
|
№ |
x0 |
x1 |
x2 |
x1x2 |
x12-2/3 |
x22-2/3 |
y |
План типа 2k |
1 |
+ |
+ |
+ |
+ |
+1/3 |
+1/3 |
y1 |
2 |
+ |
- |
- |
- |
+1/3 |
+1/3 |
y2 |
|
3 |
+ |
+ |
- |
- |
+1/3 |
+1/3 |
y3 |
|
4 |
+ |
- |
+ |
+ |
+1/3 |
+1/3 |
y4 |
|
«Звезд ные точки» |
5 |
+ |
+ |
0 |
0 |
+1/3 |
-2/3 |
y5 |
6 |
+ |
- |
0 |
0 |
+1/3 |
-2/3 |
y6 |
|
7 |
+ |
0 |
+ |
0 |
-2/3 |
+1/3 |
y7 |
|
8 |
+ |
0 |
- |
0 |
-2/3 |
+1/3 |
y8 |
|
Нулевая точка |
9 |
+ |
0 |
0 |
0 |
-2/3 |
-2/3 |
y9 |
Т к матрица ортогональная, то коэффициенты регрессии определяются независимо друг от друга по формуле:
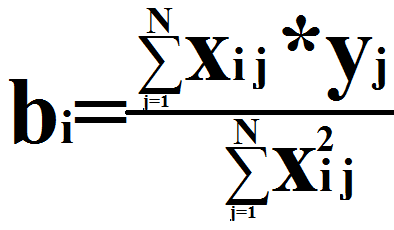
i – номер столбца;
j – номер опыта (строки).
Рототабельное планирование 2го порядка.
Информация о поверхности отклика, получена при ортогональном планировании 2го порядка, различна в разных направлениях.
Начиная эксперимент мы не знаем какое направление будет представлять больший интерес. Разумным является использование центральных композиционных планов, отвечающих требованиям рототабельности, т е план, позволяющий получить модель способную предсказать значение параметра оптимизации с одинаковой точностью, независимо от направления на равных расстояниях от центра плана.
Рототабельность композиционного плана достигается выбором величины звездного плеча α.
Для ядра содержащего полный факторный эксперимент α=2k/4, для ядра содержащего дробную реплику α=2(k-m)/4.
Для рототабельного планирования 2го порядка важное значение имеет выбор числа опытов в центре плана.
Данные для построения рототабельного центрального композиционного плана 2го порядка:
-
Число факторов
«Ядро» плана
Число точек ядра nя
Число звездных точек n2
Число нулевых точек n0
Величина звездной реплики планирования α
Общее число опытов №
2
22
4
4
5
1,414
13
3
23
8
8
6
1,682
20
4
24
16
6
7
2
31
5
25
32
10
10
2,378
52
5
25-1
16
10
6
2
32
Матрица рототабельного центрального композиционного плана 2го порядка для 2х факторов.
-
№
x0
x1
x2
x1x2
x12
x22
y
1
+
+
+
+
+
+
y1
2
+
-
+
-
+
+
y2
3
+
+
-
-
+
+
y3
4
+
-
-
+
2
0
y4
5
+
+1,414
0
0
2
0
y5
6
+
-1,414
0
0
0
2
y6
7
+
0
+1,414
0
0
2
y7
8
+
0
-1,414
0
0
0
y8
9
+
0
0
0
0
0
y9
10
+
0
0
0
0
0
y10
11
+
0
0
0
0
0
y11
12
+
0
0
0
0
0
y12
13
+
0
0
0
0
0
y13
Матрица рототабельного планирования 2го порядка не ортогональны => объем вычислений при определении коэффициента регрессии велик.