- •Составители: н.И. Житникова, г.И. Федорова, а.К. Галимов
- •Введение
- •1. Краткий перечень основных понятий теории графов
- •1.1. Общие понятия
- •1.2. Понятия смежности, инцидентности, степени
- •1.3. Маршруты и пути
- •1.4. Матрицы смежности и инцидентности
- •1.5. Связность. Компоненты связности
- •1.6. Матрицы достижимости и связности
- •1.7. Расстояния в графе
- •1.8. Образ и прообраз вершины и множества вершин
- •1.9. Нагруженные графы
- •1.10. Деревья и циклы
- •2. Решение контрольных задач
- •2.1. Компоненты сильной связности ориентированного графа
- •Алгоритм выделения компонент сильной связности
- •2.2. Расстояния в ориентированном графе
- •Алгоритм поиска минимального пути из вв ориентированном графе
- •2.3. Минимальный путь в нагруженном ориентированном графе
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе d из vнач в vкон.( vнач ≠ vкон)
- •2.4. Эйлеровы циклы и цепи
- •Алгоритм выделения эйлерова цикла в связном мультиграфе с четными степенями вершин
- •2.5. Минимальное остовное дерево
- •Алгоритм выделения минимального остовного дерева в неориентированном нагруженном графе g
- •2.6. Задача о коммивояжёре
- •3. Задания для самостоятельного решения
1.10. Деревья и циклы
Граф G называется деревом если он является связным и не имеет циклов.
Граф G называется лесом если все его компоненты связности - деревья.
Свойства деревьев:
Следующие утверждения эквивалентны:
1) Граф G есть дерево.
2) Граф G является связным и число его ребер ровно на 1 меньше числа вершин.
3) две различные вершины графа G можно соединить единственной (и при этом простой) цепью.
4) Граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один и притом простой цикл
Утверждение 4. Если у дерева G имеется, по крайней мере, 1 ребро, то у него найдется висячая вершина.
Утверждение
5.Пусть G
связный граф, а
![]() − висячая вершина вG,
граф
− висячая вершина вG,
граф
![]() получается из G
в результате удаления вершины
получается из G
в результате удаления вершины
![]() и инцидентного ей ребра. Тогда
и инцидентного ей ребра. Тогда
![]() тоже является связным.
тоже является связным.
Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.
Пусть G
– связный граф. Тогда остовное дерево
графа G
должно содержать n(G)-1
ребер. Значит, для получения остовного
дерева из графа G
нужно удалить
![]() ребер.
ребер.
Число
![]() называетсяцикломатическим
числом графа
G.
называетсяцикломатическим
числом графа
G.
2. Решение контрольных задач
2.1. Компоненты сильной связности ориентированного графа
С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.
Cоставляем
матрицу смежности A(D)
размерности
![]() (n−
количество вершин) для данного
ориентированного графа: она состоит из
нулей и единиц, номера строк – индексы
вершин , из которых исходят дуги, номера
столбцов – индексы вершин, в которые
дуги входят (если есть дуга, исходящая
из вершины vi
и входящая в vj,
то элемент матрицы смежности, стоящий
на пересечении i-той
строки и j-того
столбца равен 1, иначе – 0.).
(n−
количество вершин) для данного
ориентированного графа: она состоит из
нулей и единиц, номера строк – индексы
вершин , из которых исходят дуги, номера
столбцов – индексы вершин, в которые
дуги входят (если есть дуга, исходящая
из вершины vi
и входящая в vj,
то элемент матрицы смежности, стоящий
на пересечении i-той
строки и j-того
столбца равен 1, иначе – 0.).
Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D) ориентированного графа по первой формуле утверждения 3, затем находим матрицу сильной связности S(D) ориентированного графа (она должна быть симметрической) по второй формуле из того же утверждения.
Алгоритм выделения компонент сильной связности
1.
Присваиваем p=1
(p
− количество
компонент связности),
![]() .
.
2. Включаем в множество вершин Vp компоненты сильной связности Dp вершины, соответствующие единицам первой строки матрицы Sp. В качестве матрицы A(Dp) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из Vp.
3. Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если не остается ни одной строки (и столбца), то p- количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как Sp+1, присваиваем p=p+1 и переходим к п. 2.
Пример
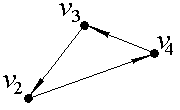
Выделим компоненты связности ориентированного графа, изображенного на рис. 6. В данной задаче количество вершин n=5.
Рис. 6.
Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом
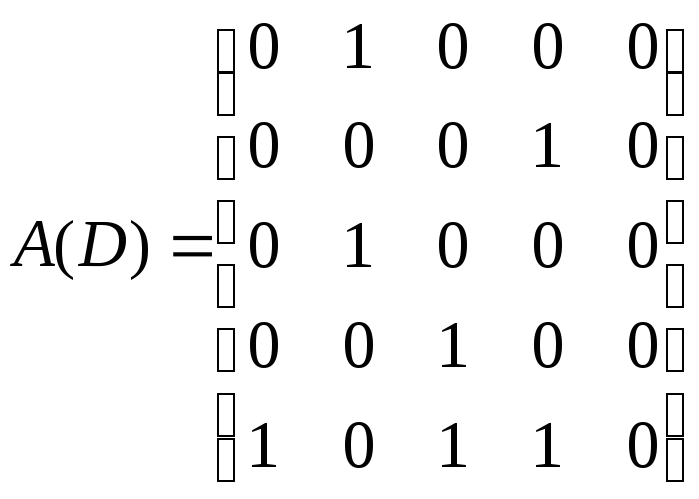 .
.
Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения 3:
 ,
,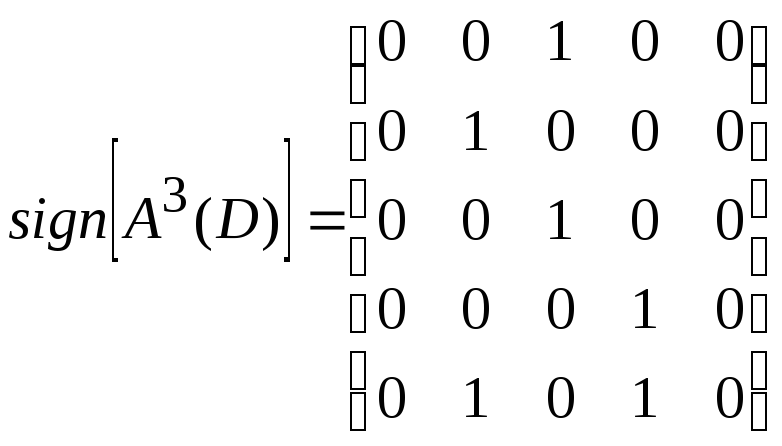 ,
,
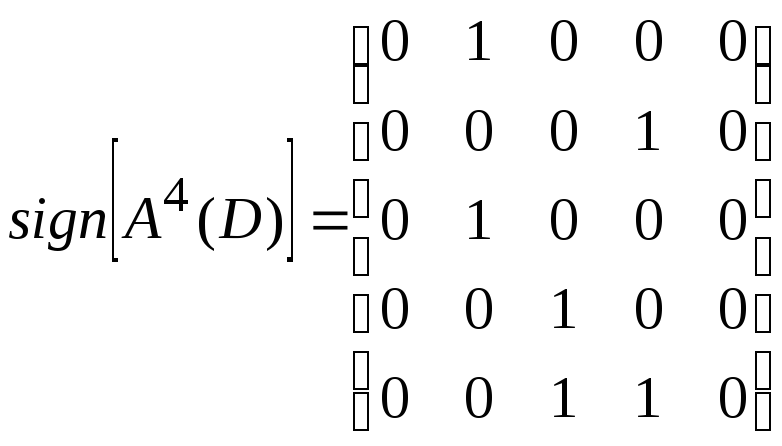 ,
,
Следовательно,
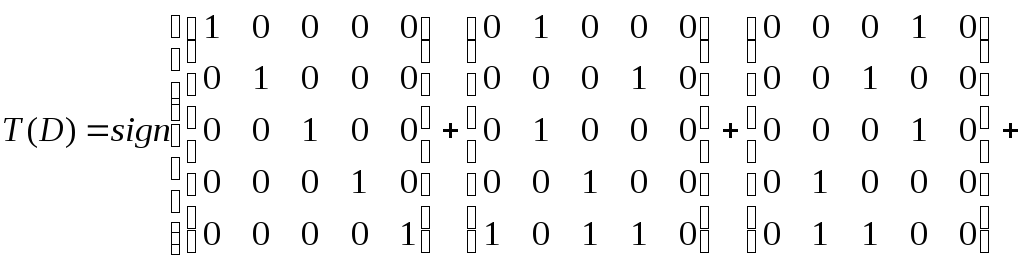
 .
.
Таким образом, матрица сильной связности, полученная по формуле 2) утверждения 3, будет следующей:
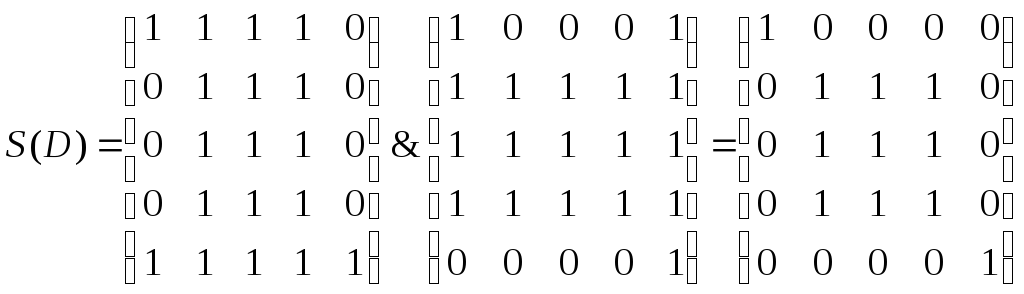 .
.
Присваиваем
p=1
![]() и составляем множество вершин первой
компоненты сильной связностиD1:
это те вершины, которым соответствуют
единицы в первой строке матрицы S(D).
Таким образом, первая компонента сильной
связности состоит из одной вершины
и составляем множество вершин первой
компоненты сильной связностиD1:
это те вершины, которым соответствуют
единицы в первой строке матрицы S(D).
Таким образом, первая компонента сильной
связности состоит из одной вершины
![]() .
.
Вычеркиваем из матрицы S1(D) строку и столбец, соответствующие вершине v1, чтобы получить матрицу S2(D):
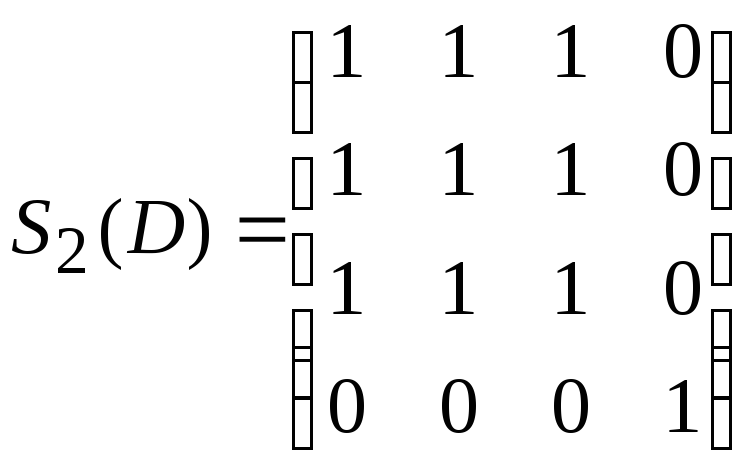 .
.
Присваиваем p=2.
Множество вершин второй компоненты
связности составят те вершины, которым
соответствуют единицы в первой строке
матрицы S2(D),
то есть
![]() .
Составляем матрицу смежности для
компоненты сильной связности
.
Составляем матрицу смежности для
компоненты сильной связности![]() исходного графаD
− в ее
качестве возьмем подматрицу матрицы
A(D),
состоящую из элементов матрицы A,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из
V2:
исходного графаD
− в ее
качестве возьмем подматрицу матрицы
A(D),
состоящую из элементов матрицы A,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из
V2:
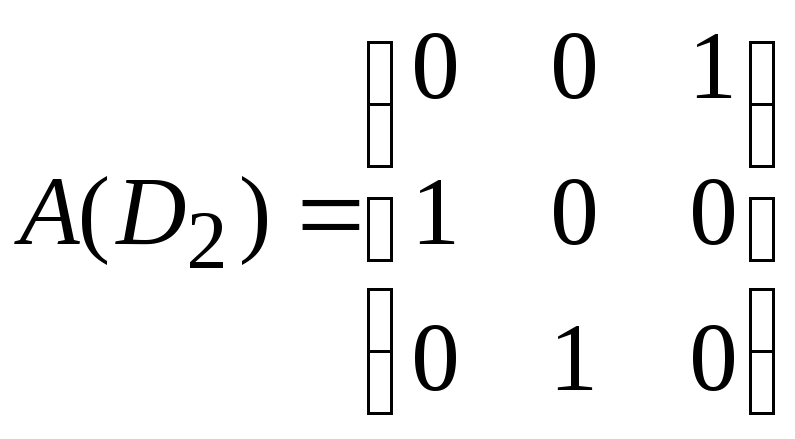 .
.
Вычеркиваем из матрицы S2(D) строки и столбцы, соответствующие вершинам из V2 ,чтобы получить матрицу S3(D), которая состоит из одного элемента:
![]()
и присваиваем p=3.
Таким образом, третья компонента сильной
связности исходного графа, как и первая,
состоит из одной вершины
![]() .
.
Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:
|
D1:
|
D2:
|
D3:
|