Молекула гелия

Когда имеется система, состоящая из 2 атомов, в ней совершаются колебания атомов с характерной энергией . Слабое притяжение является следствием силы Ван-дер-Ваальса. Так как атомы в молекуле не зафиксированы, всегда имеют место квантовые флюктуации, которые мы обозначим через . В молекуле гелия квантовые флюктуации превосходят среднее расстояние между атомами. Таким образом, кристаллическое состояние оказывается недостижимым. Даже при очень низких температурах гелий остается в жидком состоянии (за исключением больших давлений 30 атм).

Одно из важнейших свойств многоатомных молекул – возникновение анизотропии взаимодействия. Благодаря анизотропии возможна запись информации (ДНК, РНК и т.д.). Именно она сыграла решающую роль в возникновении и многообразии органических форм жизни.

Перечислим основные типы химических связей:

1. Ван-дер-Ваальсово взаимодействие;

2. ионная связь;

3. ковалентная связь.

Молекулам присущи колебательные спектры, электронные спектры и вращательные спектры.

Лекция 15.04.2009.

Модели парамагнетиков и ферромагнетиков связаны с ориентацией спина и с обменным взаимодействием, которое имеет кулоновскую природу. Энергия взаимодействия принимает два значения

Q – A j = 1

Q + A j = 0

Пусть имеется кристаллическая решетка в изотропной модели Гейзенберга для ферромагнетика. Рассмотрим любые 2 спина электронов:

Пусть j = 1 , = - матрицы Паули

Пусть j = 0 =

С данными процессами связаны явления сверхтекучести и сверхпроводимости (фазовые переходы второго рода).

В кристалле, в силу его резкой анизотропии, мы имеем следующее выражение для взаимодействия

В антиферромагнетиках есть 2 подрешетки.

Взаимодействие между молекулами. Типы химической связи.

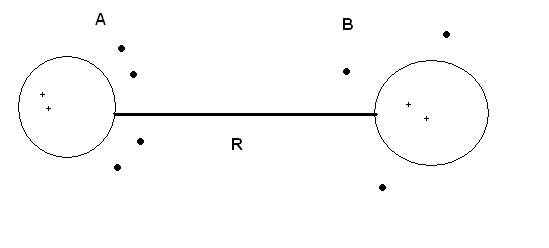
Энергия взаимодействия 2 атомов стремится к нулю на больших расстояниях между ними. За счет взаимодействия образуются связанные состояния.

Универсальный механизм взаимодействия – взаимодействие Ван-дер-Ваальса.

У молекул среды под действием внешнего поля возникает поляризация и дипольные моменты. Например, для двух атомов А и В - и , энергия связи .

Используя теорию возмущений, можно вычислить соответствующие поправки к энергии

- основное невозмущенное состояние

, n, m – известные квантовые числа

= , где суммирование ведется по всем возбужденным состояниям.

Данный эффект есть притяжение за счет флуктуаций дипольного момента.

Ковалентная и ионная связи.

NaCl – ионная связь

В этой молекуле электрон слабо связан с ядром, и есть две заряженные подсистемы: и

На малых расстояниях возникает отталкивание за счет ядер

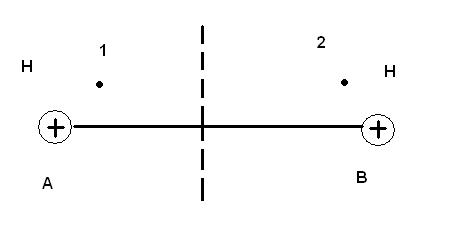
Образуется связанное устойчивое состояние.

соответствует возникшей молекуле .

Притяжение возможно за счет взаимодействия электронов.

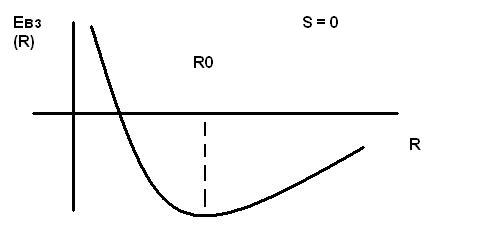
Есть плоскость симметрии, в ней отрицательное облако с максимальной электронной плотностью (при суммарном спине равном нулю). Если суммарный спин равен 1, то электронная плотность мала.

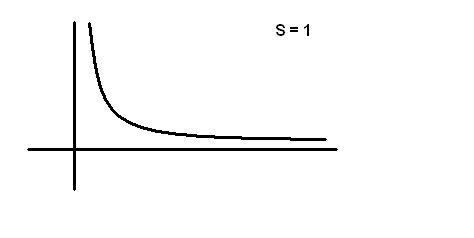
S=0

- интеграл перекрытия

У молекул есть колебательный и вращательный спектры

Отношение масс электрона и ядра задает порядки величин и частот

Сделаем некоторые оценки:

Пусть a – размер атома

- электронный спектр

- колебательный спектр

- вращательный спектр

Лекция 20.04.2009.

Элементы релятивистской квантовой теории.

Мы должны пересмотреть основные принципы квантовой механики с учётом специальной теории относительности. Для начала рассмотрим соотношение неопределённостей.

Этот постулат говорит нам следующее: не все физические величины могут быть измеримы одновременно. Запишем соотношение неопределённостей для импульса и координаты (в одномерном случае):

В нерелятивистской квантовой механике предполагается, что если физические величины одновременно измеримы, то их можно померить с любой степенью точности. Как изменится это приближение с учётом релятивистской механики?

Рассмотрим соотношение неопределённостей для энергии:

Т.е. если процесс изменяется за какой-то промежуток времени, то энергию этого процесса можем характеризовать с конечной определённой точностью.

Пусть энергия зависит от p, т.е. . Тогда, очевидно,

Из соотношения неопределённостей получаем:

Скорость не может быть больше скорости света c, поэтому:

Таким образом, если в нерелятивистской квантовой механике импульс можно измерить сколь угодно мгновенно, то теперь за промежуток времени измеряется с конечной точностью.

Кроме того, другая особенность, связанная с учётом релятивистской механики, состоит в следующем, что есть энергия и импульс, связанная с массой покоя: , больше чем эти значения, энергия и импульс не могут быть.

Подставляя «предельны» импульс, который может быть, в соотношение неопределённостей:

А это есть комптоновская длина волны. То есть в релятивистской квантовой механике можно измерить координату не точнее, чем комптоновская длина волны. Если мы имеем область с размерами меньше комптоновской длины волны, то не можем заставить локализоваться частицу в такой области.

Что же является первичным: частица или поле? Согласно классической физике, электромагнитное поле мы знаем (из уравнений Максвелла), а объектом является частица (?), которая характеризуется координатой и импульсом (?).

Гейзенберг считал, что первичным является поля, а частицы – кванты полей.

Но позже стала преобладать другая точка зрения – первичным является частица, а поле – как объект, который позволяет описать состояние частиц.

Релятивистские уравнения …

Напомним, что из симметрии пространства следуют свойства квантового момента. Он полностью переносится и в релятивистскую квантовую механику, без какого бы то ни было ограничений. Далее, согласно теореме Паули (разве?), частицы с полуцелым спином подчиняются статистике Ферми - Дирака, а с целым – статистике Бозе - Эйнштейна. И поля, с которыми мы имеем дело – либо ферми-, либо бозе- поля. Отметим, что спин – это не релятивистское понятие, а вводится в «обычной» квантовой механике. Поэтому и в релятивистском случае теория моментов выглядит также.

Квантовая теория частиц с полуцелым спином. Теория Дирака.

Запишем полный механический момент частицы, он состоит из орбитального и спинового моментов:

Мы выводили уравнение, учитывающее спин электронов. Мы должны учитывать дополнительную степень свободы и к полному набору добавить число, отвечающее за спин:

Либо:

Введём матрицу Паули: , где – безразмерный оператор.

Из коммутационных соотношений следует:

Выберем представление, в котором:

Единичная матрица:

Свойства, которые характеризуют матрицы Паули:

Так как гамильтониан должен содержать все переменные, должны включить также и переменные спина:

Поскольку у нас есть две величины и , а из них можно организовать скаляр при помощи скалярного произведения.

Такой способ позволяет получить уравнение Паули. Пока нет взаимодействия частиц с полями, ничего нового нет. Теперь включим взаимодействие:

Паули предложил такой гамильтониан:

Таким образом, наличие спина позволяет описать процессы, связанные с наличием спина . (?)

Можно ввести оператор магнитного момента:

Правильность этого выражения доказана на опытах Штерна и Герлаха.

Оно позволяет записать результат, полученный Дираком.

Вспомним релятивистскую инвариантность в классическом случае – это единственно пространственно-временных переменных, которые образуют четырёхмерное пространство.

Это свойство должно выполняться и в квантовой механике. Рассмотрим уравнение Шрёдингера, оно первого порядка:

В классической механике:

Обобщим этот результат на случай квантовой механики:

И можем писать уравнение движения (надо это предложение?). Тогда в уравнение Шрёдингера будут слагаемые вида , т.е. будет нелокальная теория. Формально, будет первый порядок по t, а по p будут все порядки, релятивистская инвариантность нарушается. Мы должны подкорректировать выражение для гамильтониана.

Далее релятивистские теории для частиц с целым и полуцелым спинами будут отличаться.

Подставим в гамильтониан:

В этом случае можно извлечь корень, если ввести матрицы, подобные матрице Паули.

Спин-переменная принимает два значения.

Введём матрицы, имеющие те же перестановочные соотношения, что и матрицы Паули:

Они коммутируют также.

Тогда запишем гамильтониан следующим образом. По импульсам гамильтониан должен быть линейным. Например,

Можно проверить (в обратную сторону), что это равенство выполняется.

Таким образом, мы решили проблему релятивистской инвариантности. Пишем уравнение Шрёдингера для свободной частицы (и в координатном представлении частицы):

– двухрядные матрицы. Совместно – будет матрица четырёхкратная:

Иногда пишут так: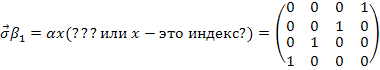

Это есть прямое произведение двухрядных матриц.

Где 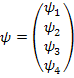– вектор-столбец, здесь уже 4 компоненты в отличие от нерелятивистской квантовой механики.

Рассмотрим простейшие следствия. Спектр частицы в свободном пространстве. А каковы интегралы для свободной частицы? Очевидно, импульс (любая проекция импульса), например . Какие ещё есть интегралы движения? Полный момент:

Доказать самим, что или . (надо записать уравнение Гейзенберга в этих переменных)

Рассмотрим спектр, должны записать уравнение в нерелятивистском случае:

.

Так как импульс – интеграл движения, можем записать частный случай (выбрав соответствующую систему координат)

Тогда:

Имеем два значения энергии в собственной системе координат.

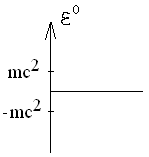
Что такое отрицательная энергия???

Можем написать так:

Тогда получаем для энергии:

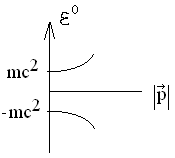
Дирак интерпретировал это так.

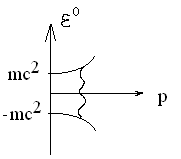
Если состояние на верхней ветке неустойчивое, частица может перескочить на нижнюю и излучить. Паули предположил, на нижней ветке все места заняты, согласно принципу Паули электрон не может перейти на нижнюю ветвь. А может ли быть обратный процесс?

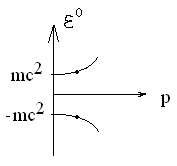
Тогда рождается частица и что-то ещё (это позитрон, по закону сохранения заряда у него противоположный знак).

Зададимся вопросом, насколько справедливо одночастичное уравнение Шрёдингера (уравнение Дирака)?

Обоснование: одночастичное релятивистское состояние в теории поля – основа, там в основе это уравнение Дирака.

А имеет ли смысл решать задачи в рамках одночастичной модели? Оказывается, некоторые задачи решаются точно.

Заметим, что вместо уравнения Шрёдингера можно писать уравнения типа уравнения Гейзенберга.

Собственные значения оператора скорости равны

Для собственные значения равны (?)

Можно также показать, что

Таким образом, получен точный результат. Шрёдингер записал точное решение уравнения Гейзенберга частицы в свободном пространстве

Осцилляция дипольного момента будет с частотой

Далее,

Этот результат получил Шрёдингер. Если осцилляции быстрые, то впереди коэффициент почти ½. Появилась нелокальность, за счёт этого есть запаздывание.

Какие задачи имеют точное решение?

Пусть есть однородное постоянное магнитное поле. . Спектр значений – уровни Ландау релятивистского электрона Дирака (?).

Если есть однородное постоянное электрическое поле – есть особенность, где потенциальная энергия станет (бесконечно?) большой, происходит рождение электрон-позитронной пары(?).

Если движение происходит в скрещенных полях – тоже известно точное решение.

Ещё один случай – сферически симметричный потенциал: .

Далее, рассмотрим электрон в поле в вакууме. Проблема в том, что исходная частица поля…(?)

Если правильно учтём взаимодействие частиц, расходимости не будет.

При искорени частица должна излучать.

Далее рассмотрим релятивистскую теорию атома водорода.

,

Т.к. взаимодействие определяется зарядом электрона, малость взаимодействия заложена именно в нём.

Стоит отметить если наступает особенность.

Какие у нас здесь величины?

- имеет особенность, характеризуя собственный момент электрона.

Можем сформировать такие скалярные величины:

Пусть хотим написать с учётом сферической симметрии. Интегралами движения являются следующие величины.

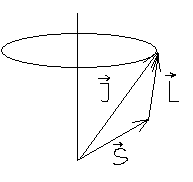
сохраняется, сохраняется, ещё можно задать - проекция тоже сохраняется.

Для замкнутой системы с учётом сферической симметрии:

Обязательно получится, что j – полуцелые значения принимает, это неудобно.

Почему последнее слагаемое имеет именно такой вид?

Возводя их в квадраты и сложив, получим искомый результат.

Можно написать:

Добавим ¼:

(+1/4?)

Хотим, чтобы это была сумма квадратов. Если есть величины

Вычислим произведение: .

Сомножитель в последнем слагаемом связан с вращением.

Перепишем и воспользуемся свойством матриц Паули.

Напишем, если A=L, B=L.

Заметим, что если в классике , то в квантовой механике это не так, (различные проекции не коммутируют)!

То, что в скобках, оказывается, некий оператор , он имеет собственные значения, кратные , т.е. они .

Эта особенность не изменится, если умножим оператор на . Обозначим:

Это есть спиновый оператор момента. Почему здесь стоит ?

Должны … коспоненты по , которые … по X и Y?

Мы покажем, что

Нужно спроектировать гамильтонман.

Множитель добавили, чтобы отнормировать на единицу скалярное произведение.

Такой оператор обладает свойством:

Заметим, поэтому:

Лекция 27.04.2009.

Аналогия полнейшая с классической задачей:

Всегда удобно сопоставить что-то с классическим вариантом.

Радиальный импульс является эрмитовским оператором:

В чем же отличие релятивистской задачи? Когда мы окончательно использовали сферическую симметрию в нерелятивистском атоме, то всё определяется квадратом орбитального момента, потому что полным моментом является орбитальный момент. Спин не входит в полный момент в задаче о нерелятивистском атоме, поэтому и интегралом движения является орбитальный момент.

Запишем волновую функцию для сферически симметричного нерелятивистского Гамильтониана:

Подставим её в гамильтониан и получим уравнение для радиальной функции:

Нечто подобное получается и в релятивистской задаче. Волновая функция стационарного состояния:

является интегралом движения для релятивистской задачи. Оператор действует по сути дела в четырехмерном спиновом пространстве (спин и изоспин - некие внутренние степени свободы). Запишем оператор координат электрона:

Итак:

Заметим, что в гамильтониан входят двухрядные матрицы, например:

Значит и должна быть двухрядной матрицей.

Таким образом мы получаем в отличии от нерелятивистской задачи систему уравнений для и , которые связаны между собой. В нерелятивистской задаче есть вантовые числа: Особенность релятивистской задачи в том, что спектр тоже дискретный и квантовые числа тоже связаны между собой, но уже с учетом спина.

определяет спектр значений энергии и принимает целочисленные значения, так как

Покажем, что спектр энергии вырожден по :

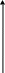
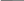
2p^3/2

2s 2p^1/2

Заметим, что . Таким образом, даже в релятивистской задаче остается вырождение по энергии, связанное с особенностью кулоновского взаимодействия. Важным открытием оказалось то, что уровни 2s и 2p^1/2 имеют разные линии. Это открытие было сделано Лэмбом в 1947 г. (смещение Лэмба).

Запишем значение энергии в нерелятивистском пределе:

С релятивистскими поправками:

Отсюда видно, что

Теперь попробуем более просто получить релятивистские поправки исходя из гамильтониана.

Точный гамильтониан электрона находящегося в потенциальном сферическом поле:

Найдём уровни энергии и стационарные состояния для релятивистской частицы:

Так как двухрядные матрицы, имеет 4 компоненты.

Когда мы подействуем на , получим систему уравнений:

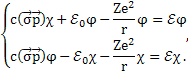
Теперь из второго уравнения выразим и подставим в первое уравнение.

Получим точное уравнение для без всяких приближений:

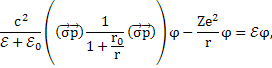
является основным параметром в релятивистской теории. Если положить , то получим нерелятивистскую задачу.

Причём для каждого уровня энергии своё значение массы.

Учтем сферическую симметрию и спроецируем уравнение на :

Воспользуемся свойством:

Тогда:

Фундаментальный малый параметр, который здесь присутствует - . Если построенная теория правильная, то при мы должны получить уравнение Шредингера для нерелятивистского атома водорода. Казалось бы, это не очевидно, так как зависит от :

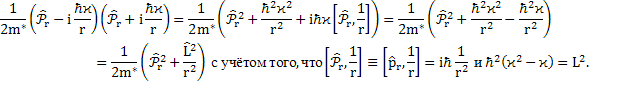
Получили обычное нерелятивистское уравнение Шредингера. Теперь проделаем туже операцию при наличии малого параметра:

Лекция 29.04.05

Спектр релятивистского атома задается квантовым числом

При этом полный момент является интегралом движения

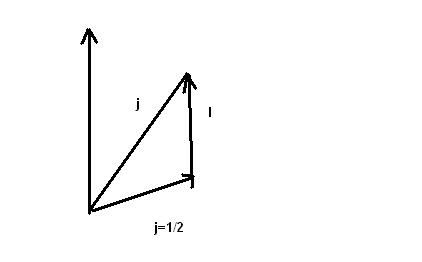
Т.к. заданному соответствуют различные значения , то имеет место вырождение

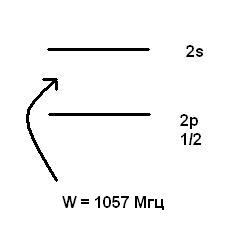
Мгц – есть такой сдвиг, если на малых расстояниях нарушается з-н Кулона

На электрон действует поле «вакуума», и кулоновское взаимодействие «размазывается»

,

Выполняются соотношения:

- постоянная тонкой структуры

Спектр свободной частицы:

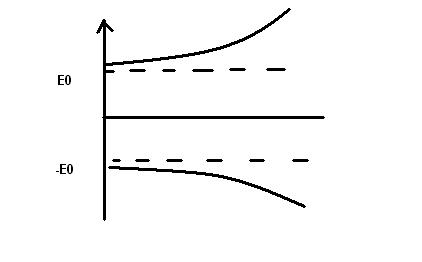
Стационарное уравнение Дирака: , где

Для радиальной волновой функции в сферически симметричном потенциале:

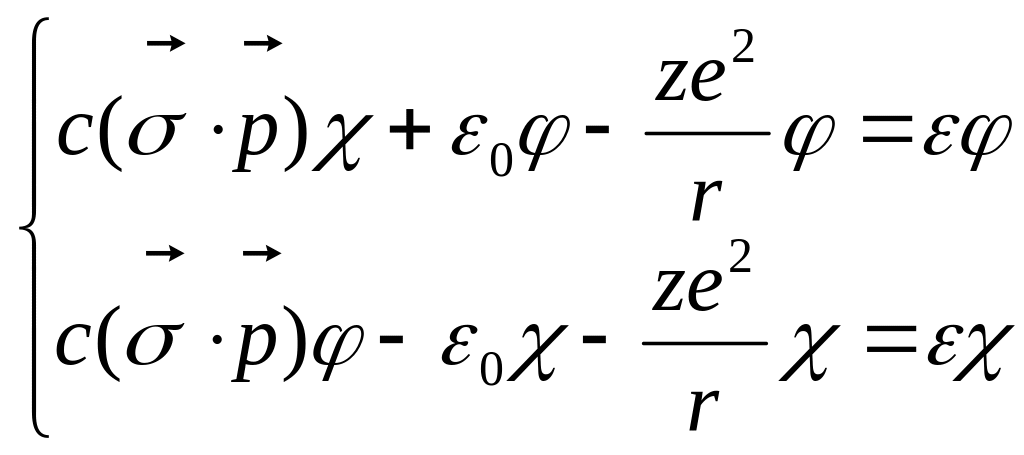
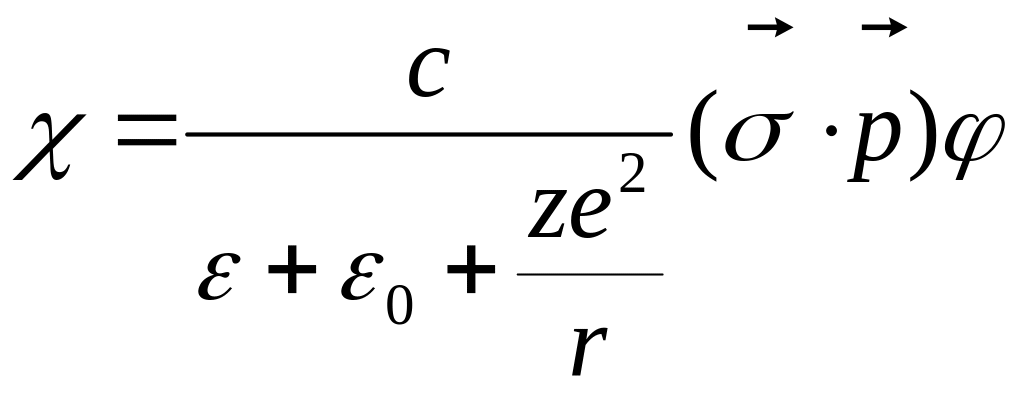
- для каждого уровня энергии есть своя масса

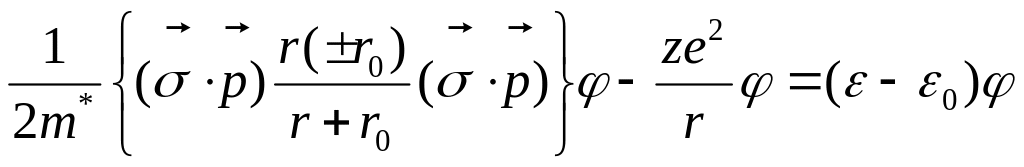
- классический радиус электрона (малая величина)

Как энергия зависит от ?

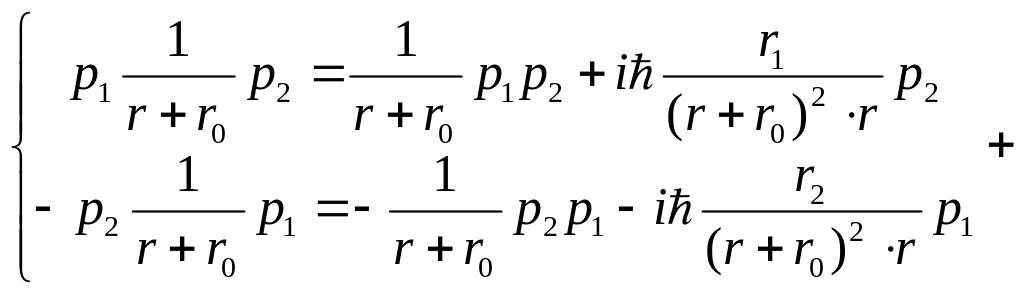
, где - гиромагнитное отношение спинового момента

То есть для электрона взаимодействуют 2 магнитных диполя, это спин-орбитальное взаимодействие

При этом происходит расщепление s и p подуровней

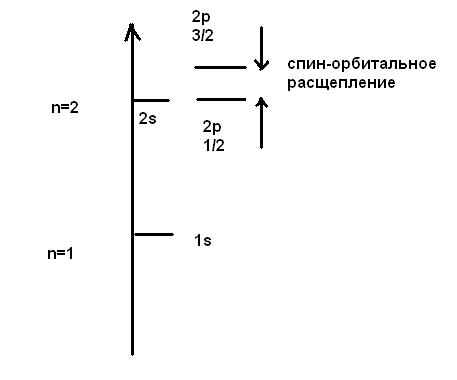
Лекция 04.05.2009.

Квантовая теория поля.

Чтобы построить квантовую теорию поля, нужно опираться на одночастичные состояния. Понятия поля и частицы, как мы уже отмечали, наиболее фундаментальные. Поля и частицы могут как-то взаимодействовать.

Современная квантовая теория поля.

Напомним, что частица может рассматриваться как квант поля. К процессам взаимодействия относятся рождение и уничтожение частиц. Отметим, существуют ферми-поля и бозе-поля.

На данный момент наиболее разработанной является квантовая электродинамика (поскольку электромагнитное взаимодействие является наиболее важным и это более простая теория).

Поля, связанные с электроном: электрон-позитронное поле(?).

Независимо можно строить теорию ферми- и бозе-полей. Рассмотрим первые.

Фок предложил:

Обозначим состояние в ξ-представлении: Считаем, - гамильтониан в этом представлении.

Запишем уравнение Шрёдингера:

Есть состояния:

Существуют тождественные частицы, и когда их много, возникают интересные эффекты.

Напомним, для ферми частиц справедливо:

Отсюда вытекает характер заполнения. Число ферми-частиц в квантовом состоянии: Статистика Ферми-Дирака – состояние свободно, либо занято, а какая частица где, не можем сказать.

Для вакуума можем записать состояние следующим образом: Дираквёл это обозначение.

Подействуем на вакуум оператором числа частиц: но ничего не изменится, так как частиц нет. Пусть есть частица в каком-то состоянии:

Статистика в явном виде не срабатывает (?).

Может быть такая ситуация:

Могут быть все состояния заняты:

Это исходный базис, в котором можно рассматривать состояние. Это пространство Фока или пространство чисел заполнения.

Каждое из состояний является собственным вектором оператора числа частиц, примеры:

Пусть частицы не взаимодействуют – это случай так называемого свободного ферми-поля.

Есть динамический принцип: в бесконечно удалённый момент взаимодействия нет, оно адиабатически включается.

Напишем гамильтониан системы в случае свободного поля в этом же базисе, в этом же представлении:

Можно перечислить все возможные значения энергии, которые принимает гамильтониан. Происходят переходы из одного базисного состояния в другое. Эти переходы нужно как-то описывать.

По определению, введём оператор состояния (например, из 1 в 2):

Назовём - оператор рождения, он рождает частицы при .

Введём обратный оператор, сопряженный оператору рождения:

Все процессы взаимодействия можно представить как рождение частиц одного сорта и уничтожение другого. Для ферми-поля эти операторы должны обладать соответствующими свойствами.

Пусть рождаются две частицы. Подействуем на вакуумное состояние:

Далее подействуем оператором

Сначала действует и только потом !

А теперь вспомним, что мы рассматриваем ферми-частицы. Перестановка частиц местами должна менять знак состояния:

Так как состояние получено при действии оператора рождения, плюс учтём свойства нечётности, поэтому, действуя, получаем:

Отсюда следует соотношение:

Запишем последнее равенство через коммутатор:

Предположим: Тогда , дважды родить частицу нельзя. Аналогично для оператора уничтожения:

Отметим другие свойства. Уничтожение и рождение частицы:

Т.е. оператор, который … число частиц (?).

Поэтому оператор числа частиц запишется следующим образом:

Можем и так записать:

Таким образом,

Если имеем дело с ферми-частицами, то антикоммутатор операторов рождения и уничтожения равен единице.

Обычно это записывается так:

Отступление: вспомним:

Можем обобщить таким образом:

Запишем гамильтониан системы:

Вспомним, что H получен из решения уравнения Шрёдингера для отдельной частицы.

Можно написать тождество (?):

Образуем оператор (?):

непрерывная переменная.

Можно предположить, что

Можем написать операторы рождения и уничтожения в различных базисах.

Можно написать для … :

Получилось такое уравнение. Смысл вторичного квантования: если в одночастичной квантовой механике имеем дело с волновой функцией, зная , можем вычислить в состоянии (вычислить состояние?).

Можно рассматривать нерелятивистский электрон. Одночастичное состояние … уравнение Дирака … . (?)

Гамильтониан для поля:

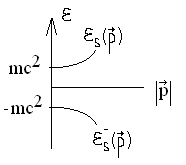
Для верхней веточки:

Если есть возможность, лучше переформулировать теорию, чем использовать отрицательную энергию.

(рисунок)

Вспомним:

И в этом случае:

Т.к. как энергия меньше или равна 0, напишем:

(?)

И тогда

Подставим в исходный гамильтониан:

Т.к. как электрон – заряженная частица, оказывается у частиц будет заряд +. Эти частицы – позитроны.

Проблема бесконечной энергии.

Основная характеристика, которая вычисляется – функция Грина.

Лекция 11.05.2009.

В этой лекции речь пойдет о квантовой теории Бозе полей. Согласно принципу тождественности все частицы, с которыми мы имеем дело в квантовой механике делятся на два класса: частицы Бозе и частицы Ферми. Соответственно существуют Ферми поля и Бозе поля. Как правило, взаимодействие между Ферми и Бозе полями определяют наиболее существенные закономерности в квантовой области. Мы построим теорию, используя подход, основанный на принципе тождественности частиц.

Построение квантовой теории основано на одночастичных состояниях. Набор одночастичных состояний тождественных частиц мы обозначаем так:

Бозе частицы отличаются от Ферми частиц тем, что четность относительно перестановки таких частиц равна +1. Это просто записать, если взять простое состояние двух одинаковых частиц:

Перестановка частиц местами дает то же самое состояние. Эта четность и предопределяет самые глубокие свойства Бозе частиц любой физической природы независимо от того, являются ли частицы релятивистскими или рассмотренными в нерелятивистском приближении. Самая существенная особенность тождественных частиц заключается в том, что мы не имеем права говорить, какая из частиц находится в том или ином физическом состоянии. Важно указать, как заполняются эти состояния и сколько частиц могут в них находиться. Поэтому основной физической величиной в связи с этим является количество частиц, находящихся в данном квантовом состоянии. Будем обозначать это таким образом: - число частиц в состоянии . Основная особенность Бозе частиц заключается в том, что их может быть любое количество в данном квантовом состоянии. Это и называется статистикой Бозе-Эйнштейна.

Теперь поговорим о том, как задавать эти состояния. Наиболее экономный вариант был предложен Фоком: Совокупность таких собственных векторов операторов числа частиц образует пространство чисел заполнения или пространство Фока.

Самые главные свойства, которые вытекают из принципа тождественности и исследования статистики Бозе-Эйнштейна, состоят в тех особенностях, которые мы обязаны наблюдать в процессах взаимодействия полей (т. е. как происходит рождение и уничтожение частиц). Чтобы описывать такие процессы нужно связать состояния с разным количеством частиц. Для этого определим такой оператор, который переводит данное состояние в состояние, в котором число частиц уменьшается на 1. По определению, пусть это будет оператор, который переводит один вектор в другой вектор:

Коэффициент с определяется из свойства Бозе частиц. Заметим, что также можно ввести и сопряженный оператор:

Теперь из этих двух определений мы можем ввести оператор числа частиц. Для этого подействуем оператором на :

Выберем таким, что бы выполнялось , тогда оператор числа частиц: