Лекция 18.02.2009

Принцип тождественности одинаковых частиц. Постулат симметрии.

Рассмотрим движение в фазовом пространстве в классическом случае. Пусть по одной траектории движется частица 1, по какой-то другой – частица 2. Мы их никогда не перепутаем и можем проследить, по какой траектории движется каждая из частиц. А что будет, если мы рассматриваем два электрона в случае квантовой механики?

Пусть эти два электрона оказались в элементарном фазовом объёме

Нельзя сказать, какой из электронов 1, а какой 2. Электроны принципиально неразличимы. Другой пример – принцип суперпозиции (для физически неразличимых альтернатив). Пусть в результате взаимодействия две частицы рассеялись, возникла квантовая интерференция неразличимых частиц, она будет зависеть от их сорта.

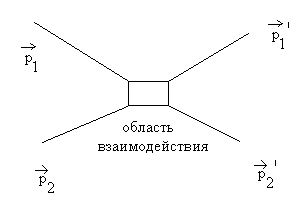
Таким образом, есть какая-то симметрия частиц. Мы их переставили местами, а ничего не поменялось.

Пусть поведение частицы описывается полным набором Например, в качестве такого полного набора можно взять Зададим два полных набора (для двух частиц) и Волновая функция системы этих частиц будет зависеть от и : Эта система описывается гамильтонианом То есть, если мы переставим частицы местами, ничего не изменится. Введём оператор перестановки частиц. По определению, . Очевидно, можем записать: т.е. это оператор симметрии. Кроме того, Раз так, если операторы физических величин коммутируют, у них общий полный набор собственных функций. Найдём собственные числа введённого оператора. Нетрудно показать, что И как следствие, есть два собственных числа

Если будет симметричная функция:

Если будет асимметричная функция:

Тождественные частицы разделились: одни описываются волновыми функциями чётности +1, другие – асимметричными функциями.

Если операторы коммутируют с гамильтонианом H, чётность сохраняется, а это закон сохранения вероятности.

Если чётность волновой функции равна +1 – это бозе-частицы, если чётность равна -1 – ферми-частицы.

Лекция 02.03.2009.

В природе существует два класса частиц – бозе-частицы (чётность волновой функции равна +1) и ферми-частицы (чётность равна -1). Это постулат асимметрии.

Пусть есть две ферми-частицы. Как же они заполняют состояния?

Итак, для этих частиц справедливо

Пусть частицы не взаимодействуют. Ясно, что они не могуь заполнять состояния таким образом:

Чтобы «примирить» частицы с принципом асимметрии, должны взять суперпозицию волновых функций с учётом чётности:

Проверим справедливость последнего утверждения, то есть будет ли эта комбинация асимметричной функцией? Подействуем оператором :

Т.е. всё правильно. Пусть имеется одна частица в состоянии и вторая – в состоянии .

для данного состояния, это состояние занято. Аналогично, Пусть состояние свободно, т.е. и т. д.

Т.е. мы изобразили некоторое состояние с определённым числом частиц.

Дирак ввёл следующее обозначение:

Число частиц, которое может быть в том или ином состоянии – это фундаментальная физическая величина. Можем сопоставить её оператор Какие собственные значения у этого оператора?

Зададимся вопросом, может ли в одном состоянии находиться две ферми-частицы? Если в выражении

вместо пишем и запихиваем тем самым две ферми-частицы в одно состояние, то и получим Таким образом, такого состояния быть не может. Две частицы нельзя запихнуть в одно квантовое состояние. Состояние может быть либо свободным, либо занятым одной частицей. Это принцип запрета Паули. Получили статистику Ферми – Дирака – в данном квантовом состоянии может быть 1 или 0 частиц. Рассмотрим возможные ситуации заполнения частицами состояний.

Физический вакуум:

Если появилась одна частица: 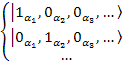- это одночастичные состояния.

Далее, рассмотрим двухчастичные состояния:

Есть трёхчастичные состояния и т. д. Может быть ситуация, когда все состояния заполнены: Подчеркнём ещё раз, что в случае ферми-частиц нельзя сказать, в каком состоянии находиться «первая» частица, в каком – «вторая» и т. д.

Теперь рассмотрим бозе-частицы и статистику Бозе - Эйнштейна.

В этом случае справедливо:

Рассмотрим две частицы: с волновыми функциями . Сколькими различными способами можно заполнить два состояния?

Существует такая возможность: .

Существует и другая возможность:

Ещё одна возможность: .

Пусть заполнили первое и второе состояния бозе-частицами, но какая где находится – сказать не можем. Заметим, . Таким образом, если перестановка частиц местами не меняет знак волновой функции, то в любом состоянии может быть сколько угодно частиц – это статистика Бозе – Эйнштейна.

Лекция 04.03.2009.

Приближенные методы решения задач квантовой механики.

Метод возмущений.

Суть метода заключается в следующем. Пусть есть поля (кванты полей). В нулевом приближении можно рассматривать как невзаимодействующие частицы и поля, а возмущение – это некоторое взаимодействие.

Следует отметить, что существует стационарная теория возмущений и нестационарная (к последней можно отнести следующую задачу: падает электромагнитная волна, найти квантовые переходы).

Стационарный метод возмущений.

Рассмотрим постановку задачи. Пусть есть решение какой-то известной задачи и обозначим H₀ – гамильтониан невозмущённой системы. В частности, мы знаем стационарные состояния и уровни энергии, зная решение уравнения:

H₀ φ_n⁰ = ε_n⁰ φ_n⁰ (1)

Пусть нам известны состояния системы φ₁⁰, φ₂⁰, φ₃⁰, … и соответствующие им значения энергии: ε₁⁰, ε₂⁰, ε₃⁰, … . Задача состоит в том, чтобы учесть слабое воздействие на систему.

Обозначим V – дополнительное слабое взаимодействие, тогда гамильтониан возмущённой системы выглядит следующим образом:

Ĥ = Ĥ₀ + V (2)

Задача теории возмущений – найти новые состояния и новый спектр значений энергии.

Ĥψ = (Ĥ₀ + V)ψ = εψ (3)

В качестве примера можно указать атом водорода, помещённый в некоторое электрическое или магнитное поле.

Следует отметить, в этом методе есть одна важная особенность. Она обусловлена тем, что в невозмущённой систему к данному значению энергии может относиться несколько состояний. (это так называемая вырожденная задача). От этого зависит способ решения задачи.

Стационарная теория возмущений при отсутствии вырождения.

Из-за дополнительно малого возмущения уровни энергии смещаются. Следует ожидать, эти смещения будут малыми по сравнению с расстояниями между уровнями. Качественно это можно проиллюстрировать следующим образом:

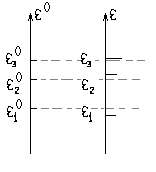Следует отметить, что теория возмущения работает не всегда. Например, известно, что явление сверхпроводимости в металле обусловлено взаимодействием электрона проводимости с колебаниями атомной кристаллической решётки, которым соответствует квазичастица, названная фононом. Казалось бы, взаимодействия между ними почти нет, но нельзя получить характеристики этого явления с помощью стационарной теории возмущений.

Вернёмся к нашей задаче. Итак, нам известны уровни энергии и стационарные значения энергии невозмущённой системы. Надо найти, что будет после взаимодействия. Прежде всего, зададимся вопросом, в каком представлении будем решать задачу?

Заметим, состояния представляют собой полный набор и естественно представить любое состояние как суперпозицию базисных. Но и при наличии взаимодействия

ψ=∑с_nφ_n ⁰ (4)

ⁿ

В возмущённой системе возникает перемещение состояний, величина которого зависит от величины взаимодействия. Т.к. невозмущённые состояния известны, состояние ψ задаётся коэффициентами c_n:

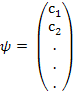
Следовательно, мы имеем дело с матричный методом.

Стационарное уравнение Шрёдингера в матричной форме.

Наиболее просто эта задача решается в системе базисных векторов. Уравнение Шрёдингера в матричном виде

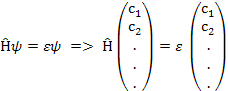
Т.е. квадратная матрица действует на одностолбцовую. Или можем записать:

Очевидно, это уравнение можем спроектировать на любой из векторов φ_n:

Мы считаем базисные вектора нормированными. Если они относятся к различным значениям, они ортогональны, т.е. :

Вся физика заключена в матричных элементах оператора энергии.

Ĥ = Ĥ₀ + V

И, по определению,

= = представим матричный элемент в собственном представлении , поскольку невозмущенная матрица диагональна в собственном представлении.

Мы также обязаны вычислить матричный элемент взаимодействия:

И мы можем окончательно записать стационарное уравнение Шрёдингера в матричной форме, с учётом того, что Ĥ = Ĥ₀ + V и :

Роль малого параметра будет играть матричный элемент возмущения. Его оставим в одной стороне, остальное перенесём в другую:

Т.е. исходный гамильтониан действует как матрица.

Или, окончательно:

Формулировка метода возмущений.

Отметим, что возможны ситуации, когда решение оказывается точным, например, может оказаться, матрица возмущений диагонально, и мгновенно получим спектр новых состояний.

В общем случае нужно искать решения, разлагая искомые величины в ряд по малому параметру:

Аналогично:

Подставим эти выражения в стационарное уравнение Шрёдингера и приравняем слагаемые одинаковых порядков. Найдя одно приближение, находим приближение более высокого порядка.

Итак, нужно для начала задать нулевой порядок. До включения взаимодействия система находилась в конкретном состоянии с энергией . Включили взаимодействие, произошло смещение уровня и надо найти его методом теории возмущёний.

В нулевом приближении:

Можем написать первый порядок, зная нулевой, приравнивая слагаемые первого порядка малости:

Т.к. , получаем:

Может быть m=l, m≠l, это текущий индекс, можем им распоряжаться, в отличие от n.

Пусть m=l. В первом приближении:

, это есть средние значение возмущения по невозмущённому состоянию, т.е. диагональный элемент. В первом порядке уровень сместится как среднее значение возмущения, т.е. .

Из этого результата имеем ещё важный случай: если m≠l, второе слагаемое обращается в ноль и получим результат, как изменится стационарное состояние (не только уровни энергии). Поправка первого порядка к волновой функции и скобка ≠0, можем поделить и получим:

В знаменателе стоит разность невозмущённых значений энергии. Перепишем для любого n, n≠l:

Проделаем процедуру для второго порядка. Опять исходим из стационарного уравнения Шрёдингера:

+…

Для более высокого порядка нужно выписать слагаемые в …, мы их не выписываем. Далее находим вторую поправку. Опять, либо m=l, либо m≠l.

где штрихом отражено то обстоятельно, что суммирование ведётся по всем индексам n, кроме n=l. И поправка к невозмущённому состоянию (при отсутствии вырождения):

Знак поправки зависит от знака знаменателя. Правильно напишем, если знаем, что основное состояние (поправка второго порядка) будет меньше нуля, он должен сместиться вниз, если l соответствует состоянию с наименьшей энергией.

Теория возмущений при наличии двух близких уровней. Двухуровневое приближение (двухуровневая идеализация).

Пусть есть два избранных состояния, близкие, остальные далеки.

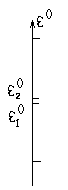
, m ≠1,2.

Такая ситуация характерна для многих задач, эта особенность связана с эквидистантностью спектра. Из формулы получаем, что большая величина и этим слагаемым можно пренебречь:

Как видно из формулы, нижний уровень сместится вниз, а верхний – вверх. Раз такая ситуация имеет быть, можно говорить в этом случае об идеализации двухуровневой системы. Оказывается, можно ожидать и точный результат в случае двухуровневой системы.

Двухуровневая система. Точное решение.

Пусть существует всего два независимых, невозмущённых состояния.

Других состояний нет.

Т.е. эту задачу можем решить точно.

- знаем, получим определитель второго ранга.

Пишем стационарное уравнение Шрёдингера в случае, когда диагональные элементы отсутствуют:

Или, в эквивалентном виде:

Эта система имеет нетривиальное решение, если её определитель равен нулю.

Отсюда получаем:

Дополним до полного квадрата и в итоге получим:

Пример. Эффект Штарка.

Пусть атом находится во внешнем электрическом поле. Тогда, очевидно:

,

где ε – напряжённость электрического поля, d – дипольный момент двухуровнего атома.

Заметим, d₁₂ = (d₂₁)^*=d.

На основании вышеописанного примера, получим параболическую зависимость, переходящую в линейную.

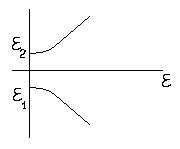
Лекция 16.03.2009.

Теория возмущений при наличии вырождения.

Рассмотрим исходную «невозмущённую» задачу:

α пробегает значения, соответствующие кратности вырождения

Из опыта ясно, эти вырожденные состояния при наличии возмущения перемешаются наиболее сильно и возникает такая задача:

Или: (

Опять, разложим состояние по базисным состояниям невозмущённой системы, соответствующие уровням с одинаковыми значениями энергии:

Подставим это выражение в уравнение Шрёдингера, аналогично невырожденному случаю, получим:

Это однородная система уравнений, она имеет нетривиальное решение, если её определитель равен 0, то есть:

Таким образом, произойдёт расщепление состояний:

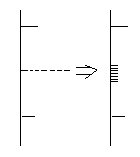
Метод расчёта электронных состояний кристаллических решёток.

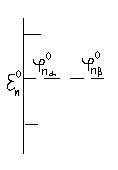
Уровни энергии в изолированном атоме (на рисунке также изображён кулоновский потенциал ядра):

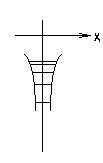
Сблизим таким атомы настолько, чтобы они образовали кристаллическое состояние.

Изобразим наиболее вероятное положение ядер, они на самом деле совершают колебательные движения, но в нулевом приближении мы считаем ядра неподвижными. Заметим, на каждый атом действует периодический потенциал.

Рассмотрим некоторые особенности.

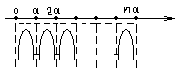
Электроны, находящиеся на уровне, обозначенном штриховой линией, скользят по «горбушкам» потенциала, они чувствуют их слабо. Например, электроны в атомах Na, K ведут себя таким образом. И поэтому можно рассматривать потенциалы ядер как небольшие возмущения для таких электронов (т.н. приближение слабой связи).

Отметим, есть и противоположная ситуация – каждый электрон почти «связан» (т.н. приближение сильной связи).

Запишем гамильтониан для отдельного электрона в периодическом поле:

где v(x) – потенциал в точке с координатой x=0, v(x – n a) – потенциал в точке с координатой x = n a.

Поскольку мы имеем дело с периодическим потенциалом:

постольку волновые функции должны подчиняться теореме Блоха.

Запишем уравнение Шрёдингера, с учётом трансляционной симметрии:

Вспомним свойство блоховских состояний:

Как обычно, должны считать возмущения малыми. В нулевом приближении:

, т.е. мы имеем дело со свободным электроном. Далее:

Таким образом, данному значению энергии соответствуют два состояния с импульсами p и –p. Обозначим их: . Волновая функция невозмущённого состояния представляет собой волну де Бройля.

Заметим, есть две возможности: рассматривать бесконечный кристалл или достаточно большой, но конечный, но в этом случае надо задать ещё и граничные условия.

Итак, с учётом нормировки,

Рассмотрим простейшую периодическую функцию:

Очевидно, , если

k – это т.н. период обратной решётки.

Теперь должны вычислить матричный элемент по невозмущённому состоянию:

Ясно, что: .

Если матричные элементы между некоторыми состояниями равны нулю, перемещения не будет, если не раны нулю – то будет. Это обстоятельство напоминает двухуровневую систему. Согласно её идеализации, целесообразно искать решение в таком виде:

И, подставив, получаем:

Что же мы должны ожидать? Когда возмущение стремится к нулю, это свободный электрон, плоская волна. Затем, задали рябь, потенциал, появилась огибающая волны от нуля до какого-то значения и возникает энергетическая щель – зона состояний в любом периодическом потенциале.

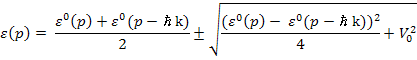
Наиболее сильно возмущены состояния с близкими значениями энергии:

Это особая точка импульсов, в области которых наиболее сильно перемещаются состояния, это граница т.н. зоны Бриллюэна.

Изобразим закон дисперсии возмущённой системе. Напомним, что для невозмущённой системы он выглядит так: (парабола).

Отметим, что известны общие свойства (следуют из теоремы Блоха):

Т.е. - чётная периодическая функция с периодом С учётом этого получаем

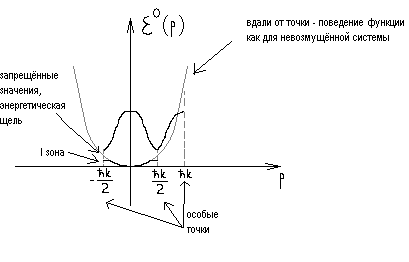
Получили зонный характер спектра.

Для решения этой задачи пользуются не только методом возмущений, но и другим – методом псевдопотенциала. Электрон не чувствует «горбушку» потенциала, поэтому находят нулевой потенциал и подгоняют решение.

Приближение сильной связи.

Ещё большую роль играет теорема Блоха в этом случае. Отметим, в 1 см³ содержится 10²³ состояний. Получаем бесконечное число вырождений. И надо будет диагонализировать бесконечнорядную матрицу. Это очень сложная задача. Как мы сейчас увидим, можно просто решить поставленную задачу, используя свойство трансляционной симметрии.

Пусть электрон находится в состоянии с энергией . Гамильтониан невозмущённой системы: . Этот же электрон может относиться к другому ядру, у которого потенциал: ) и . Далее, считаем, система невозмущённых состояний образует полную систему: . Линейная суперпозиция этих функций называется функцией Ванье.

Решение уравнение Шрёдингера:

Можем искать в виде этой суперпозиции блоховских функций невозмущённых состояний:

Это волна де Бройля, должны быть особые коэффициенты(?):

Далее, сместим n на единицу, от этого сумма не изменится:

Последние две суммы равны, если . Можно положить И тогда . Следовательно, получаем: .

Для того, чтобы доказать равенство: надо найти матричные элементы H по этим блоховским функциям. Оказывается, из трансляционной симметрии вытекает, что гамильтониан будет диагональным:

с точностью до вектора обратной решётки . Чтобы найти энергию, нужно найти среднее значение гамильтониана по блоховским функциям (при записи среднего значения используем нормировку!):

Сместим начало отсчёта и получим:

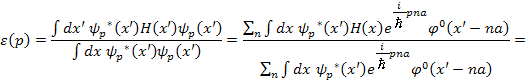
Поскольку

Затем суммы сократятся и:

I(m) – это некоторое число. I(0)=1 – нормировка. Если m≠0 – это интеграл перекрытий.

Справедливы соотношения:

I(1) играет роль основного малого параметра. Интеграл перекрытия – это «хвостик» на соседнем (?) (этот же уровень в «соседнем» потенциале ядра?) , т.к. вероятность мала, это малая величина.

Итак:

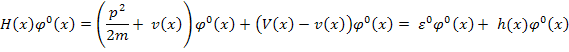
Заметим, что h(x) – мало.

В итоге:

Лекция 18.03.2009.

)

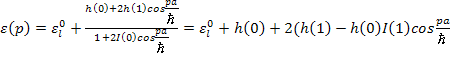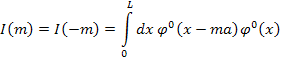
Таким образом, дискретные уровни переходят в некоторую энергетическую зону.

Заметим, что малый параметр может иметь различную природу. В задачи с приближением сильной связи используем тот факт, что вероятность туннелирования мала и поэтому пользуемся соответствующими оценочными приближениями.

Рассмотрим вопрос о количестве состояний в одной энергетической зоне. Пусть дан кристалл с характерным размером L. У нас есть ещё одна величина – период решётки. Тогда в одномерном случаем получаем, что число ячеек в кристалле определяется следующей формулой:

А в трёхмерном случае:

Где - элементарный объём. Это то число, которое мы получили, задавая квазиимпульс _{k. Также учтём ещё спин электрона:}

т.е. получили, что число состояний в одной зоне чётно.

В качестве примера рассмотрим атом K. У него есть полностью заполненные зоны, а верхняя зона заполнена частично (это металл, если наложим внешнее поле, то появится ток). Есть ещё возможность, когда число электронов нечётно – это тоже будет металл. А если число электронов, приходящихся на одну ячейку, чётно – будет диэлектрик или полупроводник. Но в силу особых свойств симметрии может возникнуть перекрытие энергетических зон, и может быть получен полуметалл.

Подчеркнём ещё раз, мы рассматривали задачу в нулевом приближении, не учитывая колебания ядер.

Рассмотрим ещё одно обстоятельство.

Пусть зависимость ε(p) имеет в пределах первой зоны Бриллюэна экстремум – минимум либо максимум.

Есть область, где импульс даёт малое значение (?), в этом случае можно пользоваться т.н. приведённом массой.

Нестационарная теория возмущений.

Для начала отметим, что в этом случае не обязательно возмущение должно явно зависеть от времени. Есть целые классы задач, которые решаются методом нестационарной теории возмущений. Во-первых, это теория квантовых переходов (выбираем неравновесное состояние, действуем светом, смотрим, какое состояние будет в итоге). Схематично это можно представить следующим образом:

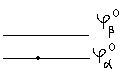
Во-вторых, другой важный класс задач связан с теорией рассеяния. Две частицы налетают друг на друга, взаимодействуют в какой-то области, а потом разлетаются. Представим этот процесс схематически:

Главный вопрос: какое будет новое невозмущённое состояние?

В-третьих, существует ещё один важный класс задач, связанный с квантовой кинетикой.

Таким образом, мы выделили три составляющих, которые могут быть рассмотрены в рамках нестационарной теории возмущений. Определим тип исходного уравнения, которое нужно положить в основу данного метода. Есть уравнение Гейзенберга, есть уравнение Шрёдингера (отметим, что квантовая кинетика – это квантовая теория броуновского движения, для которого используется уравнение Гейзенберга).

Следует отметить, что наиболее просто получить метод нестационарной теории возмущений, если взять за основу уравнение Шрёдингера. Эволюция системы задаётся гамильтонианом:

Существует две возможности: когда V зависит от t явно и неявно. Пишем уравнение Шрёдингера:

Известно состояние в исходный момент времени, как правило, выбирается t=0. Тогда требуется найти волновую функцию ψ в произвольный момент времени.

Иногда (например, в квантовой теории поля), берут за начальный момент Согласно квантовой теории поля, мы должны считать, что когда-то взаимодействие отсутствовало (это гипотеза), т.е. включение взаимодействия происходит адиабатически медленно. Будем пользоваться первым способом описания, полагая начальный момент t=0. По идеологии метода считаем, что эволюция самого возмущения известна. Сделаем ещё одно предположение: H₀ не зависит от t. Тогда можем записать (считаем возмущение отсутствует V→0, считаем решение «невозмущённой задачи известным):

Решение это уравнения нам хорошо знакомо:

Эволюция во времени, формально, определяется экспонентой. Раскладывая её в ряд Тейлора и производя операции с каждым членом, получаем искомый результат. Здесь в качестве малого параметра выступает само возмущение V и оно входит явно.

Уравнение Шрёдингера в представлении взаимодействия.

Запишем это уравнение в эквивалентном виде. Поскольку есть свободная эволюция системы, целесообразно её использовать и перебросить на переменные системы(?) (если известно решение вспомогательной задачи, его лучше сразу же использовать).

Поэтому, опираясь на вышесказанные догадки, вполне логично искать решение в следующем виде:

Подставив это решение, получим т.н. уравнение Шрёдингера в представлении взаимодействия.

Также нам хотелось бы убрать свободную энергию из уравнения:

Таким образом, одинаковые слагаемые в левой и правой частях сокращаются, чего мы и добивались. Заметим, в левой части есть небольшая «помеха» - фазовый множитель в виде экспоненты. Для того, чтобы его убрать, домножаем левую и правую части на ,

и получаем:

Т.е. V(t) уже изменился, мы перебросили на него свободную эволюцию системы:

Следует отметить, что большая часть эффектов укладывается в нестационарную теорию возмущения первого порядка приближения.

При

Зададимся вопросом: как написать уравнение Шрёдингера, чтобы учесть начальное условие? Для этого нужно проинтегрировать уравнение Шрёдингера от 0 до t и поделить на _:

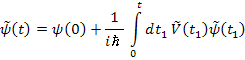
Получили уравнение Шрёдингера в интегральной форме. Также(?):

Теперь должны записать решение (следуя теории возмущений) в виде разложения по малому параметру:

Очевидно, в нулевом приближении:

Затем подставляем это разложение в левую и правую части уравнения Шрёдингера и приравниваем слагаемые одинакового порядка малости.

В случае первого порядка:

Затем для удобства переобозначим переменные:

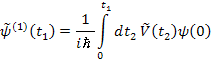
И подставляем, получив второй порядок малости:

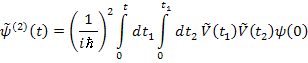
Отметим важную особенность. Мы говорили, что операторы (?) не коммутируют, поэтому важно, какой из них стоит справа. Заметим, что сначала действует оператор в более ранний момент времени (t₁ > t₂). Эта асимметрия связана с неравноценностью интегрирования по t₁ и t_2. Устраним её. Вспомним, есть т.н. единичная функция Хэвисайда, которая позволит нам строго учесть принцип причинности. Так называемая «ступенчатая» функция (или функция Хэвисайда) определяется следующим образом:

Тогда интеграл перепишется следующим образом:

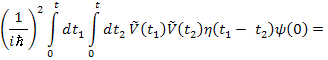
Далее, если «1» и «2» поменяем местами, то ничего не изменится, и поделим на два:

Заметим, что выполняется правило: оператор более раннего времени действует справа.

Можно ввести оператор упорядочивания по времени:

Затем экспоненты разложим в ряд (?) и для n-ного порядка получим:

Диаграммы Фейнмана.

Для описания взаимодействия частиц удобно пользоваться диаграммами Фейнмана. Рассмотрим несколько примеров.

Лекция 23.03.2009.

Пусть имеется электрон в зоне проводимости, он обладает импульсом При взаимодействии с фононом он может как испустить, так и поглотить фотон. Схематически это обстоятельство можно изобразить следующим образом:

Рассмотрим пример, где используется второй порядок теории возмущений.

Пусть электрон испускает фотон, потом опять поглощает его.

На диаграмме Фейнмана это выглядит следующим образом: Задача решается с помощью теории возмущений второго порядка.

Вспомним поляризационный эффект в твёрдом теле, масса частицы изменяется из-за взаимодействия. Электрон, взаимодействуя с внешним излучением, «меняет» свою массу. (?)

Можно рассмотреть ещё один пример.

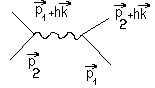
Электроны взаимодействуют: один электрон излучил квант света, другой его поглотил.

Произошёл «обмен» излучением. Этот эффект лежит в основе теории сверхпроводимости (эффект Купера).

Подчеркнём ещё раз, нестационарная теория возмущений имеет также приложения и в теории квантовых переходов, и в квантовой кинетике.

Далее будем применять нестационарную теорию возмущений к конкретным задачам.

Теория квантовых переходов.

Используем нестационарную теорию возмущений первого порядка.

Считаем, в момент времени t=0 . Т.е. в некоторый начальный момент система находилась в состоянии с энергией . Тогда:

В момент времени е система может оказаться в каком-то другом состоянии . Надо найти амплитуду перехода в новое состояние (вероятность этого перехода). В новом состоянии (?):

Вероятность того, что в момент t мы обнаружим в новом состоянии, обозначим , которая определяется следующей формулой:

При возведении в квадрат фазовый множитель даст единицу и получаем окончательно:

Этот результат можем получить для любого порядка теории возмущений. Можем пользоваться формулой лишь в теории возмущений первого порядка(?).

Отсюда находим матричные элементы:

Где - т.н. частота перехода.

Тогда получаем:

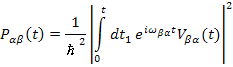
Особыми являются задачи, где внешнее воздействие – гармоническое. Рассмотрим этот случай более подробно.

Теория возмущений при гармоническом воздействии.

Этот случай наиболее важен, так как любую внешнюю силу (даже непериодическую), можно представить в виде суммы гармоник, произведя разложение в ряд Тейлора. Итак, считаем, что V(t) меняется по гармоническому закону.

(мы пишем комплексно-сопряжённое слагаемое, поскольку оператор эрмитов). Далее, пусть . Физически это означает: поглотился квант света, энергия возросла. Будут два слагаемых . У первого фаза большая, он быстро осциллирует, и даёт меньший вклад, чем последнее слагаемое, поэтому слагаемое с «плюсом» отбрасываем. С учётом этого обстоятельства запишем ответ:

, где введено обозначение: И получаем:

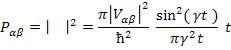
Очевидный результат при малых временах: .

Если подождать достаточно долго, при больших временах получим (и считая взаимодействие слабым), что эффект накапливается за промежуток времени:

Это смахивает на δ-функцию:

Поглотился квант , система перешла в конечное состояние. Закон сохранения энергии строго выполняется на бесконечных промежутках времени. И формула для теории рассеяния: . Аналогичные рассуждения приводят к выражению:

Зададимся вопросом, какова же полная вероятность квантовых переходов (из начального состояния во все возможные) в единицу времени?

«Золотое» правило Ферми.

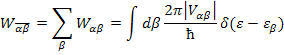
Где - усреднённый индекс. Если у нас спектр непрерывный, то мы вместо суммы должны писать интеграл.

Пусть есть некоторая поверхность постоянной энергии, когда β перпендикулярна к ней. Можем перейти к другой сфере.

Тогда интеграл равен:

Эта «знаменитая» плотность конечных состояний – для ряда значений либо большая, либо малая величина, плотности конечных состояний.

Квантовая кинетика.

Рассмотрим постановку задачи. Пусть на среду падает внешнее поле. Происходит поляризация среду, происходит взаимодействие с магнитными моментами. Считаем внешние возмущения заданными. И пусть есть какая-то система. Обозначим оператор дипольного момента . Внешнее воздействие описывается оператором (?). Тогда возмущение запишем в виде: (?). Хотим рассмотреть процессы поглащения и излучения в нашей системе.

Казалось, чтобы найти, как меняются , должны решить уравнение Гейзенберга. Можем провести рассуждения, которые мы проводили и найти искомые коэффициенты.

А можем использовать картину Шрёдингера и потом перейти к представлению Гейзенберга.

(?)

Вспомним:

И, используя стандартный переход к другой картине движения, получаем:

Таким образом, мы получили оператор в представлении Гейзенберга в отсутствии взаимодействия.

Дополнительная эволюция находится в и , находим:

Дипольный момент определяется следующим образом:

Напишем S матрицу:

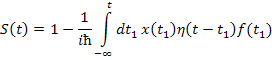
Выделим первый порядок:

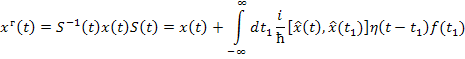
Лекция 30.03.2009.

Теперь речь пойдет о системах, состоящих из колоссально большого числа частиц, потому что всякая реальная физическая задача касается таких систем. Даже когда мы имеем дело с каким-либо маленьким кусочком вещества объемом 1см³ (содержит в себе порядка 10²³ частиц), его свойства и особенности определяются квантово-механическими закономерностями. Казалось бы, если взять более простую систему, например, атом водорода, состоящий из e^- и p⁺, вы сможете найти спектр значений энергии такой системы (все возможные стационарные состояния). Но если более внимательно отнестись к такой же простой системе, то оказывается, что с помощью динамической ситуации для двух частиц мы можем описать далеко не всё, так как система взаимодействует с полем даже при нулевой температуре, и реальное число степеней свободы такой простой системы оказывается бесконечным. По этой причине в классической физике изобретен метод описания столь сложных систем, называющийся статистической физикой. В квантовой физике этот метод можно называть квантовой статистикой, или квантовой механикой систем многих частиц. Первое с чем мы сталкиваемся, начиная изучать простые системы,- это первый постулат квантовой механики(наиболее полное описание механической системы задается некоторым вектором ). Сейчас мы придем к пониманию, что на самом деле существует ограниченный класс состояний, который можно описать с помощью вектора состояний. Ситуация подобна следующей: выделено особое состояние, которое для данной физической величины есть состояние, в котором она имеет определенное значение (собственный вектор). Так вот, оказывается, задать состояние с помощью даже очень простой системы не всегда возможно. Приведем известный пример. Представьте себе два электрона таких, что их суммарный спин равен 1. Нас будет интересовать отдельный спин. Мы хотим знать вероятность измерения спина отдельного электрона. Оказывается, что задать состояние одного из электронов этой системы с помощью волновой функции нельзя. Как быть в этом случае? Появляются особенности, которые требуют расширения первого постулата и включения в него более общего способа описания квантово-механической системы. Теперь начнем с другого конца. Приведем простую ситуацию, в которой следует расширить понятие вектора состояния. Пусть есть N электронов (для определенности 10²³). Ясно, что с точки зрения динамики мы можем задать состояние такой системы, задавая импульсы и координаты каждой из частиц. А описать ее в целом можно, задавая функцию распределения . В классической физике уравнение движения для такой функции распределения хорошо известно. Во многих случаях это кинетическое уравнение Больцмана:

,где .

Это исходное уравнение классической статистической физики. Затем, если вспомнить принцип соответствия, можно понять, что произойдет с описанием такой сложной системы в рамках классической механики. Каждой физической величине соответствует оператор , а f соответствует какой-то оператор . Следовательно, согласно принципу соответствия, состояние сложной системы в квантовой механике описывается уравнением :

.

Оператор в матричном виде называется матрицей плотности.

Матрица плотности. Чистые и смешанные состояния. Свойства диагональных матричных элементов матрицы плотности. Стационарные и нестационарные состояния. Уравнение фон Неймана.

Сейчас речь пойдет о записи среднего значения физической величины в матричном виде.

Рассмотрим две физические величины А и В.

Так как собственные вектора физической величины ортогональны, можно записать

,

а любое состояние можно записать в виде их суперпозиции

Наша задача состоит в том, чтобы любому заданному состоянию, которое описывается вектором , записать среднее значение любой другой физической величины. Можно записать так:

.

А теперь запишем в представлении оператора :

где =( ) – матричный элемент.

Идея в том, что если физические величины в матричном представлении есть матрицы, то вектор дается в виде столбца. Формально можно избежать такой асимметрии введением квадратной матрицы, описывающей данное состояние таким образом:

.

Тогда среднее значение будет выглядеть следующим образом:

А это ничто иное, как след произведения .

Итак, мы можем находить среднее значение любой физической величины, а значит, зная матрицу плотности, мы можем найти и вероятность измерения любой физической величины. Например, величины А:

– вероятность измерить значение величины А в данном состоянии.

Зачем же нужен был новый способ описания? Какие у него преимущества перед старым?

Введем понятие чистого состояния. Чистое состояние - это такое состояние, которое описывается вектором . Если это не так, то состояние называется смешанным. Введем критерий того, что данное состояние, описываемое матрицей плотности является чистым ( ). Сейчас мы увидим, что матрица плотности чистых состояний обладает свойством

.

Убедимся в этом:

Задание.

Проверить, являются ли данные матрицы плотности матрицами плотности чистых состояний:

Если ,то говорят, что состояние смешанное, и вектор состояния задать нельзя.

Теперь стоит записать уравнения движения для матрицы плотности. И поскольку мы ввели матрицу плотности для какого-то фиксированного состояния, то предположим, что пользуемся картиной Гейзенберга. В этом случае матрица плотности не зависит от времени. Запишем уравнение для динамической переменной:

Теперь вычислим среднее значение

Приведем одно важное свойство:

Циклической перестановкой получаем:

Таким образом, вся динамика определяется матрицей плотности:

Теперь можно записать уравнение для матрицы плотности:

Это и есть уравнение фон Неймана. Особенность в том, что вся эволюция во времени содержится в состоянии , а оператор физической величины не зависит от времени. Вернемся к понятию стационарного состояния. Любое стационарное состояние любой механической системы - это такое состояние, в котором вероятность измерения любой физической величины не зависит от времени. Это будет только в том случае, если матрица плотности не зависит от времени:

=

Это и есть условие стационарности. Совпадает ли это условие стационарного состояния с тем, которое мы рассматривали первоначально? В чем особенность того определения? Мы говорили о том, что состояние с определенной энергией является стационарным. Это свойство остается неизменным. Но очевидно, что могут существовать стационарные состояния и с неопределенной энергией. Например, состояние термодинамического равновесия. Состояние стационарное, а энергия подчиняется распределению Гиббса и не имеет определенного значения. Расширение понятия стационарного состояния принципиально, и мы имеем возможность сформулировать его с помощью уравнения фон Неймана.

Условие стационарности можно записать так:

.

Таким образом, произвольное состояние будет стационарным, если оно зависит только от интеграла движения.