Устойчивость внецентренно сжатой гибкой стойки.

В реальном строительстве часто не удается загрузить стойку центрально приложенной силой. Пусть эксцентриситет ее приложения e.

Расчет ведем по деформир-й схеме:

__(1)

Воспользуемся приближенным диф. уравнением изгиба.

; __(2)

;

;

; __(3)

Общее решение уравнения (3) имеет вид:

__(4)

Константы A и B определяем из граничных кинематических условий:

а) при z=0 ; .

б) при z=l ;

;

__(5)

при z=0 ;

при z=l ;

(6)

(6) - точное решение

Анализ формулы (6) показывает, что при приближении сжимающей силы к критическому значению

Однако, в действительности это не совсем так. Прогибы могут быть большими, но конечными по величине.

Это происходит потому, что в решении было использовано приближенное диф. уравнение. Если использовать точное диф. уравнение: , предстоит решить нелинейное диф. уравнение 2-ого порядка, которое дает следующие характеристики:

M_max в стержне будет в заделке:

M_max при z=0; ,

а максимальные нормальные напряжения стержня будут в той же точке с вогнутой стороны:

__(7)

=15=

Продольно-поперечный изгиб.

В условиях продольно-поперчного изгиба, т.е. одновременного действия поперечной нагрузки и продольно сжимающей силы, работают крайние колоны (сваи) каркаса здания. Стойки поддерживающие грунт в котловане и т.д.

Изгибающий момент в балке равен (1), где - изгибающий момент от поперечной нагрузки. Расчет следует вести по деформативной схеме, когда y(z)≠0. Такого рода задачи являются не линейными, т.к. из выражения (1)=>, что нельзя найти момент M не зная Y, а Y нельзя найти не зная M. Воспользуемся приблизительным дифферинцальным уравнением изгиба EIy”=-M; EIy”=-M₀-Fy (2).

Для стержня с произвольными граничными кинематическими условиями следует использовать выражение: EIy”=q, где (3).

Четыре константы, после интегрирования выражения (3) определяются из граничных условий.

Пусть: Y=Y₀+∆Y(4), где Y₀ – прогиб от поперечной нагрузки; ∆Y – дополнительный прогиб вызванный действием продольной силы.

Для прогиба Y₀ справедливо выражение: EIy₀”=-M₀ (5). Подставим выражение (4) в (2):

EI(y₀”+∆y”)=-M₀-Fy (6). Вычитаем из (6) выражение (5) получим: EI∆y”=-Fy (7). Зададимся формой изгиба в виде синусоида. В этом состоит приближенность решения задач, т.к. точное решение выражения (2) является очень сложным.

Задаваемая функция Y(z) должна удовлетворять граничным условиям . При Z=0 и Z=l; ∆y=0; ; (9). Подставим выражение (9) в (7):

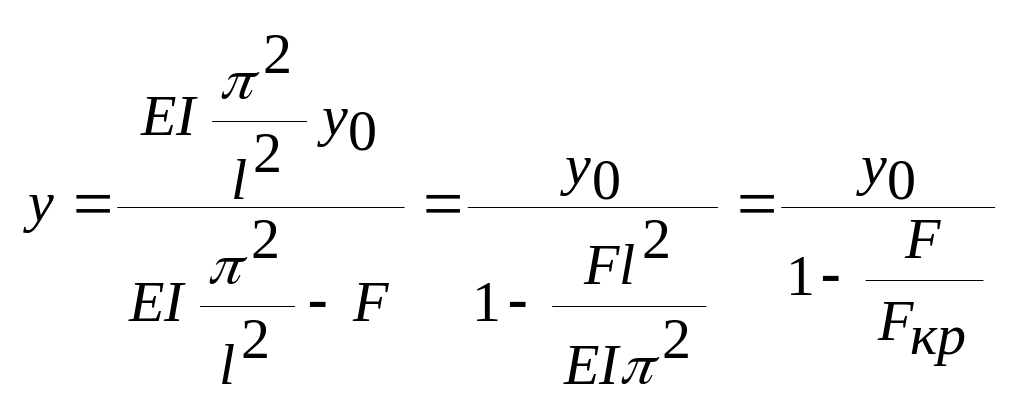. Из выражения(4): ; . => (10).

=16=

Расчет кривых брусьев. Вывод формулы нормальных напряжений при чистом изгибе.

Кривые брусья – стержни, имеющие плоскую кривую ось. Ось может быть очерчена по окружности, параболе, синусоиде, эллипсу и т.д.

Различают кривые брусья большой и малой кривизны.

а) малая кривизна

б) большая кривизна

Кривые брусья – крюки подъемных кранов, несущие конструкции в виде арок в мостах, при перекрытии больших пролетов, ребра жесткости в оболочках, тоннелях и т.д.

Несущие 2-е плоские арки, плоскости которых составляют около 25^о, они перекрывают пролет ангара, пролет арки – 180м.

Внутренние силовые факторы в кривых брусьях. (подход к сопротивлению материалов)

а) парабола

б) окружность

Чистый изгиб кривого бруса.

- чистый изгиб.

При выводе используем следующие допущения:

1) ось бруса – плоская кривая. Загружение бруса осуществляется в плоскости его оси.

2) брус симметричен относительно плоскости, в которой расположена его ось.

3) гипотеза плоских сечений.

4) продольные волокна не надавливают друг на друга.

Вырежем из кривого бруса двумя смежными сечениями его часть и рассмотрим деформацию этой части.

r₀ – радиус кривизны н.с. (0-0)

ρ - радиус кривизны волокна n-n

1’,2’,n’ – деформированное состояние части кривого бруса

Определим относительную деформацию волокна.

__(1)

__(2)

При чистом изгибе N=0, то:

; __(3)

т.к. , __(4)

, имеем:

;

, ; __(5)

Изгибающий момент равен: __(6)

, тогда: ,

__(7)

- статический момент площади сечения A относительно н.с.

, откуда: __(8)

Подставим (8) в (2):

__(9)

Эпюра нормальных напряжений в поперечном сечении изменяется по гиперболе, которая имеет 2 асимптоты:

1-параллельно оси эпюры

2-перпендикулярно оси и проходит через точку центра кривизны.

=18=