Ядро сечения. Процедура построения.
Ядро сечения – выпуклая область вокруг точки центра тяжести сечения, при приложении в пределах которой внецентренно – приложенной силы, напряжение по всему сечению возникает одного знака. Т.е. нейтральная линия находится за пределами контура сечения.
Контур ядра сечения
зависит только от контура самого сечения
и его геометрических характеристик
необратимо задаться положениями
нейтральной линией, который не делят
сечение на 2 зоны. Затем на основании
формул:
;
,
для каждой касательной находятся силы
данной нейтральной линии. Это точка
будет лежать на границе ядра сечения.
;
;
;
Пример построения.
а) прямоугольник
;
;
Положение касательной |
отрезки, отсекаемые на осях |
координаты точек ядра сечения |
Точка ядра сечения |
||
|
|
|
|
||
1-1 |
±∞ |
-h/2 |
0 |
h/6 |
1 |
2-2 |
±∞ |
h/2 |
0 |
-h/6 |
2 |
3-3 |
-b/2 |
±∞ |
b/6 |
0 |
3 |
4-4 |
+b/2 |
±∞ |
-b/6 |
0 |
4 |
б) Сплошной круг.
;
;
;
;
=9=
Плоский поперечный косой изгиб.
- это вид сопротивления, когда плоскость действия внешнего изгибающего момента не совпадает ни с одной из главных осей инерции сечения. Это сложный тип сопротивления, т.к. его можно рассматривать как одновременный изгиб бруса в 2-х плоскостях. Если при косом изгибе в поперечном сечении бруса Qx=Qy=0, такой вид называется чистым косым изгибом. Если плоскость действия внешнего момента одинакова по длине бруса, то косой изгиб будет плоским, т.е. изогнутая ось бруса – плоская кривая. Если плоскость меняет своё положение для 2-х смежных сечений, то такой вид косого изгиба пространственным, а изогнутая ось – пространственная кривая.
Рассмотрим консольную балку прямоугольного сечения.
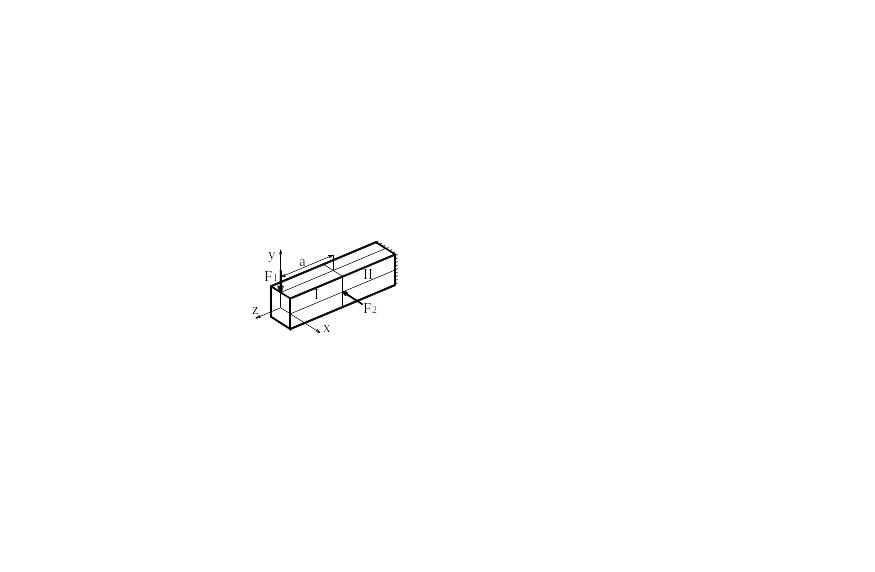
(прямой
поперечный изгиб)
(совместное
действие Mx
и My
– косой изгиб).
Используя принцип независимости действия сил, определим нормальные напряжения в поперечном сечении бруса отдельно от каждого момента.
(1)
Знак выбирается в соответствии со знаком напряжений при изгибе. При yi=xi=0 из ф-лы (1) σi=0, т.е. нейтральная линия проходит через точку центра тяжести сечения.
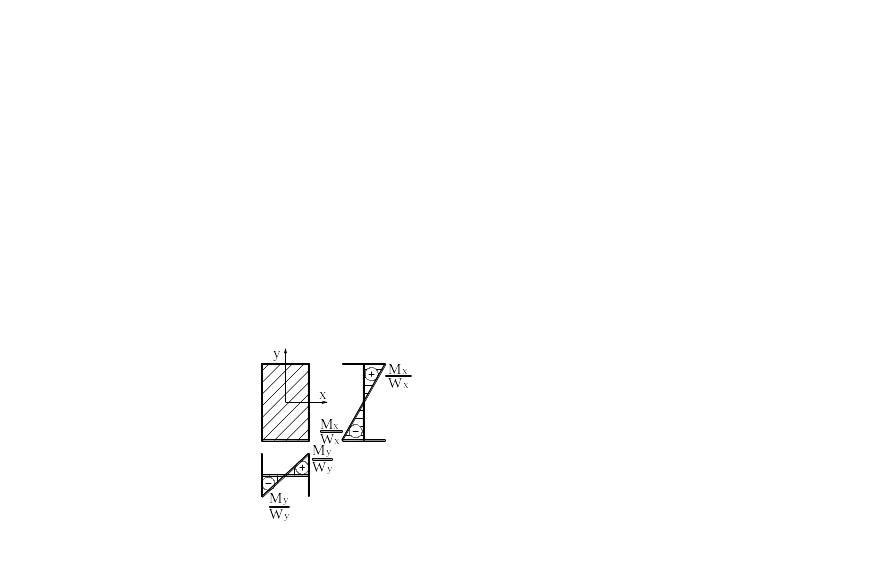
Ось y
– след плоскости действия момента Mx.
Ось x
– след плоскости действия момента My.
След действия суммарного момента
имеет угол наклона α с осью y.
Этот угол положителен, если ось y
для совмещения со следом действия
суммарного момента следует повернуть
по часовой стрелке.
(2)
Подставив (2) в (1):
(3)
Определим уравнение нейтральной линии, приравняем (3) к нулю:
(4)
y(x) – ур-ие нейтральной линии при косом изгибе.
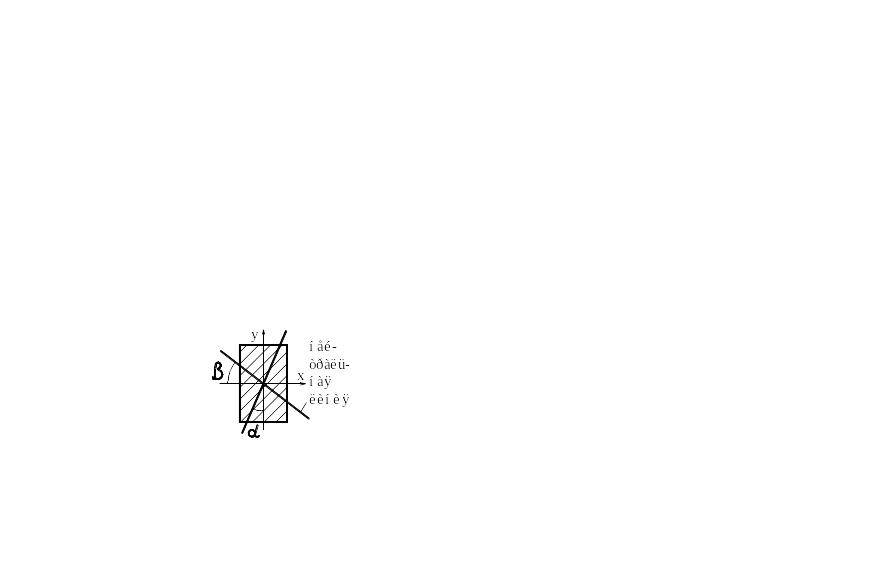
α≠β, т.е. нейтральная
линия и след действия
не
перпендикулярны в отличие от прямого
плоского изгиба.
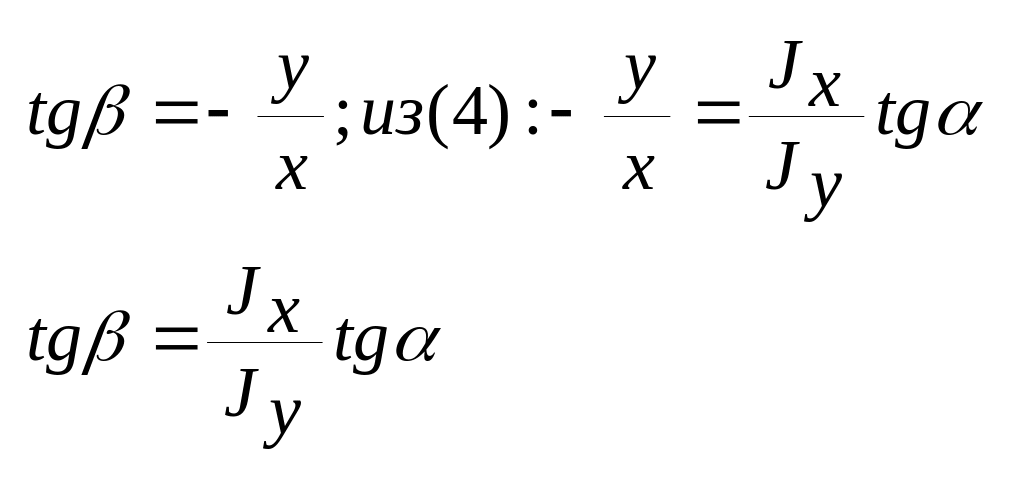(5)
β>0, если ось x необходимо повернуть для совпадения с нейтральной линией по часовой стрелке. Для круга, когда Jx=Jy: tgβ=tgα. При любом наклоне внешней силы всегда реализуется прямой плоский изгиб.
Пример: брус прямоугольного сечения с соотношением сторон h/b=5 загруженный внешним моментом, плоскость действия кот. составляет с вертикальной осью y угол α=5˚. Сравнить максимальные нормальные напряжения при заданных условиях и для случая, когда плоскость действия момента совпадает с осью y.
Решение:
Находим положение е нейтральной линии:
β=65˚>0, значит по часовой стрелке.
а) плоскость действия
момента совпадает с осью y:
б) напряжение при заданных условиях:
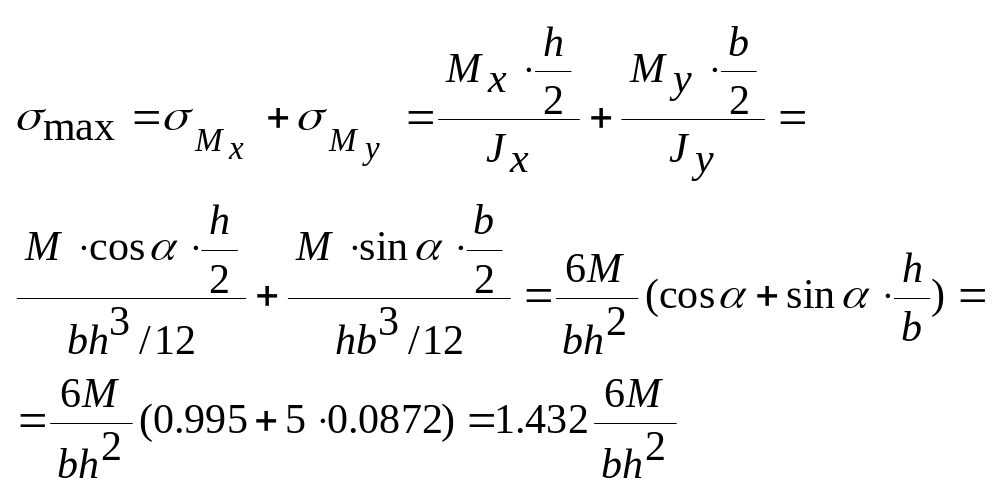
=17=
Нагрузки и воздействия, приводящие к динамическому действию на балку.
Динамическое действие – силовое воздействие, при котором кинетическая энергия оказывается соизмеримой с потенциальной. При динамическом нагружении – силы изменяются быстро, то есть меняют своё значение. К примеру
=10=