
- •Виды перемещений. Точное и приближенное дифференциальное уравнение изогнутой оси балки.
- •Ядро сечения. Процедура построения.
- •Пример построения.
- •Плоский поперечный косой изгиб.
- •Устойчивость однопролётных стержней постоянного сечения.
- •Задача Эйлера.
- •Границы применимости формулы Эйлера.
- •Устойчивость внецентренно сжатой гибкой стойки.
- •Продольно-поперечный изгиб.
- •Расчет кривых брусьев. Вывод формулы нормальных напряжений при чистом изгибе.
- •Поперечный удар. Динамический коэффициент, динамические напряжения, динамический прогиб.
- •5)Строим эпюры нормальных напряжений:
- •Ргр №6 Расчет сечения, составного из элементарных геом фигур.
- •Расчет сечения, составленного из прокатных профилей.
=1=
Виды перемещений. Точное и приближенное дифференциальное уравнение изогнутой оси балки.
Одним из важнейших этапов расчета реальных конструкций, помимо расчетов на прочность, является расчет на жесткость. Для этого необходимо знать прогибы и углы поворотов сечения балки. Под прогибом понимают линейное перемещение точки оси балки в вертикальном направлении (горизонтальным перемещением в виду относительной малости прогибов пренебрегают). Прогиб положителен, если перемещение точки происходит в направлении оси. Угол поворота сечения – угол между сечением, перпендикулярным к точке оси балки до деформации, и таким же перпендикуляром после деформации. Значение линейных и угловых перемещений необходимо для расчета статически неопределимых задач при плоском изгибе, для составления уравнений совместимости деформаций. Цель подобного рода задач – нахождение уравнения упругой линии балки.

![]()
![]()
Как видно из рисунка:
![]() (1). Строительные конструкции проектируются
с условием, что углы поворота сечений
малы и не превышают 1˚, поэтому можно
считать
(1). Строительные конструкции проектируются
с условием, что углы поворота сечений
малы и не превышают 1˚, поэтому можно
считать
![]() (2). Воспользуемся известным из курса
математики уравнением связи между
кривизной линии и ее производным в виде:
(2). Воспользуемся известным из курса
математики уравнением связи между
кривизной линии и ее производным в виде:
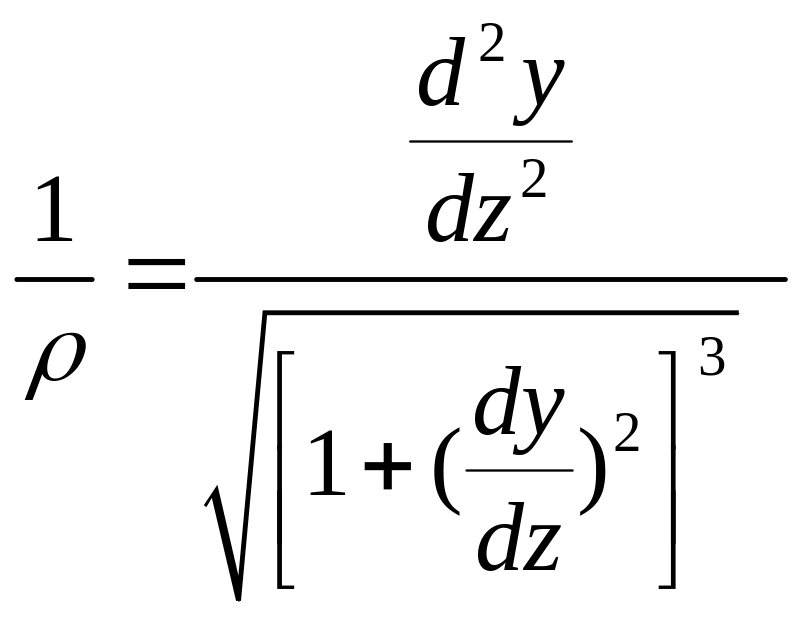 (3), где ρ - радиус кривизны. Известно, что
(3), где ρ - радиус кривизны. Известно, что
![]() (4). Из (3) и (4) получаем:
(4). Из (3) и (4) получаем:
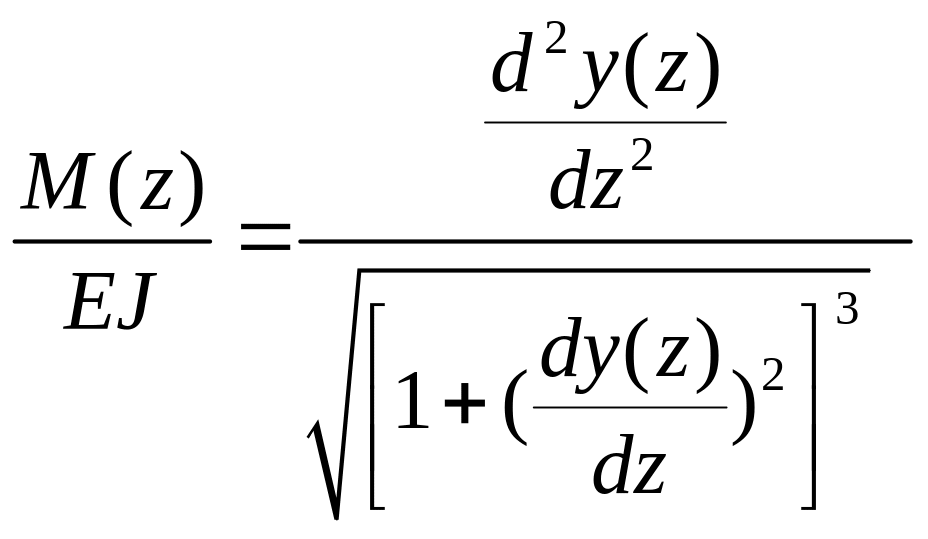 (5) – точное дифференциальное уравнение
изогнутой оси балки, применяемое в
основном для расчета конструкций при
больших деформациях. Если
(5) – точное дифференциальное уравнение
изогнутой оси балки, применяемое в
основном для расчета конструкций при
больших деформациях. Если
![]() (6) – приближенное дифференциальное
уравнение изогнутой ос балки. В общем
случае изогнутая ось балки – плоская
лекальная кривая.
(6) – приближенное дифференциальное
уравнение изогнутой ос балки. В общем
случае изогнутая ось балки – плоская
лекальная кривая.

=7=
Внецентренное растяжение-сжатие. Уравнение нейтральной линии.
Нейтральная линия – геометрическое место точек в пределах сечения бруса, напряжения в которых = 0. Нейтральная линия делит сечение на 2 зоны: растянутую и сжатую.
Определим ур-е нейтральной линии, используя формулу (1’):
![]() ;
;
![]() ;
;
![]() ;
;
![]() __(3)
__(3)
Или
![]() __(4)
__(4)
(4) - уравнение прямой линии в отрезках,
где
![]() и
и
![]() - отрезки, отсекаемые нейтральной линией
на осях инерции.
- отрезки, отсекаемые нейтральной линией
на осях инерции.
![]() __(5)
__(5)
Покажем на примере прямоугольного сечения:
!!!!!!!!!!!
Как следует из рисунка, наиболее опасные точки в сечении – точки, наиболее удалённые от нейтральной линии:
В сжатой зоне - точка А(XA;YA);
В растянутой зоне - точка В(XB;YB).
Условие прочности для материала, одинаково сопротивляющегося на растяжение и сжатие (сталь 3) записывается для наиболее удалённой точки:
1) Если Rсж = Rрастяж (сталь)=R
![]() __(6)
__(6)
2) Если материал
имеет разные сопротивления на растяжение
и сжатие (бетон, алюминий, чугун, дерево
и т.д.), т.е.
![]()
![]() __(7)
__(7)
![]() __(8)
__(8)
=2=
Метод непосредственного интегрирования приближенного дифференциального уравнения изгиба.
Из выражения
![]() (6) двукратным интегрированием получаем:
(6) двукратным интегрированием получаем:
![]() (7) – функция угла поворота сечения.
(7) – функция угла поворота сечения.
![]() (8) – функция прогибов. Константы C
и D
находят в каждом конкретном случае из
граничных кинематических условий (по
перемещениям).
(8) – функция прогибов. Константы C
и D
находят в каждом конкретном случае из
граничных кинематических условий (по
перемещениям).
Пример:
Для заданной балки определить функции прогибов и углов поворота, а также перемещения свободного конца.
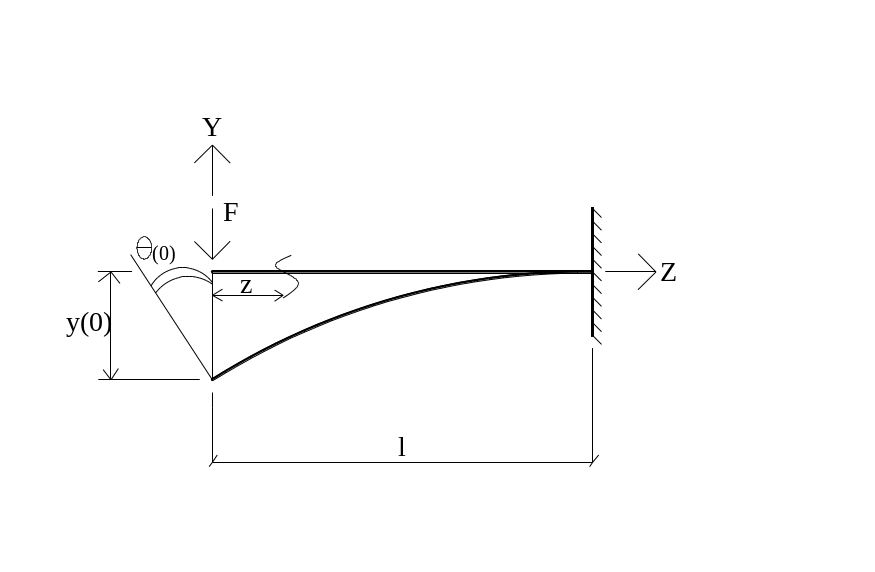
![]()
![]()
![]() .
.
при z=l![]()
![]()
![]()
![]() .
.
при z=0![]() .
.
![]() - угол поворота
сечения в начале координат.
- угол поворота
сечения в начале координат.
![]() .
.
при z=l![]()
![]()
![]()
![]() .
.
при z=0![]()
![]() .
.
Метод непосредственного интегрирования.
=3=
Графо-аналитический метод определения перемещения.
Часто нет необходимости получать расчетом выражение y(z) и θ(z), а требуется только определить перемещение в отдельных точках балки.
Он основан на
аналогии с записей:
![]() (*),
(*),
![]() (**).
Пусть задана балка с известной нагрузкой
и опорными устройствами, для которой
выполняется условие (*), пусть эта балка
будет действительной. Возьмем воображаемую
(фиктивную) балку той же длины, с пока
неизвестными опорами устройствами,
для которой справедливо выражение (**).
(**).
Пусть задана балка с известной нагрузкой
и опорными устройствами, для которой
выполняется условие (*), пусть эта балка
будет действительной. Возьмем воображаемую
(фиктивную) балку той же длины, с пока
неизвестными опорами устройствами,
для которой справедливо выражение (**).
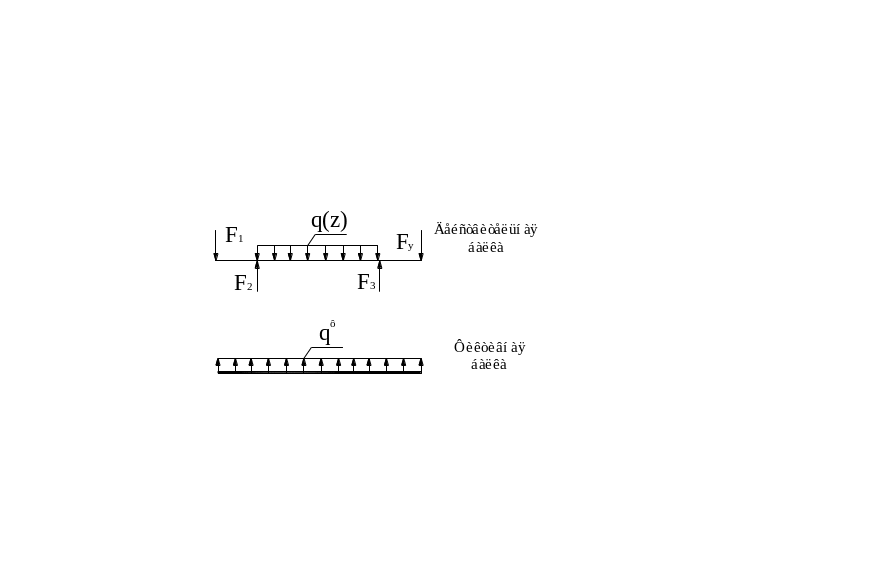
Если принять
![]() - фиктивная нагрузка.
- фиктивная нагрузка.
Эпюра моментов для действительной балки, тогда
![]() (1). После двукратного
интегрирования левой и правой части
выражения (1) получим 2 пары констант:
левая часть Сл
; Д
л. Правая
часть: Спр; Дпр. Если потребовать: Сл=Спр,
Дл=Дпр =>
(1). После двукратного
интегрирования левой и правой части
выражения (1) получим 2 пары констант:
левая часть Сл
; Д
л. Правая
часть: Спр; Дпр. Если потребовать: Сл=Спр,
Дл=Дпр =>
![]() (2).
(2).
![]() (3). Из выражения (2) и (3)=> граничные
кинематичные условия для действительной
балки должны точно соответствовать
граничным статическим условиям (условиям
по усилиям) для фиктивной балки.
(3). Из выражения (2) и (3)=> граничные
кинематичные условия для действительной
балки должны точно соответствовать
граничным статическим условиям (условиям
по усилиям) для фиктивной балки.
Пример.

EI=const,
![]() ;
;
![]() ;
;
![]()
=4=
Вывод уравнения методом начальных параметров (уравнение универсальной линии балки). Частные случаи граничных условий.
Возьмем балку с известными граничными кинематическими условиями, содержащую весь набор силовых воздействий. Условия решения:
начало отсчета (начало координат) всегда располагается в крайней левой точке оси балки;
моменты M(z) в любом случае сечения балки вычисляют как сумму моментов всех сил расположенных только слева от сечения;
скобки вида (z-a), (z-b), (z-c) – только положительны;
интегрирование выражений M(z) выполняют без раскрытия скобок;
сосредоточенный момент действующий на балку представляют в виде M=M(x-a);
компенсация распределенной нагрузки.
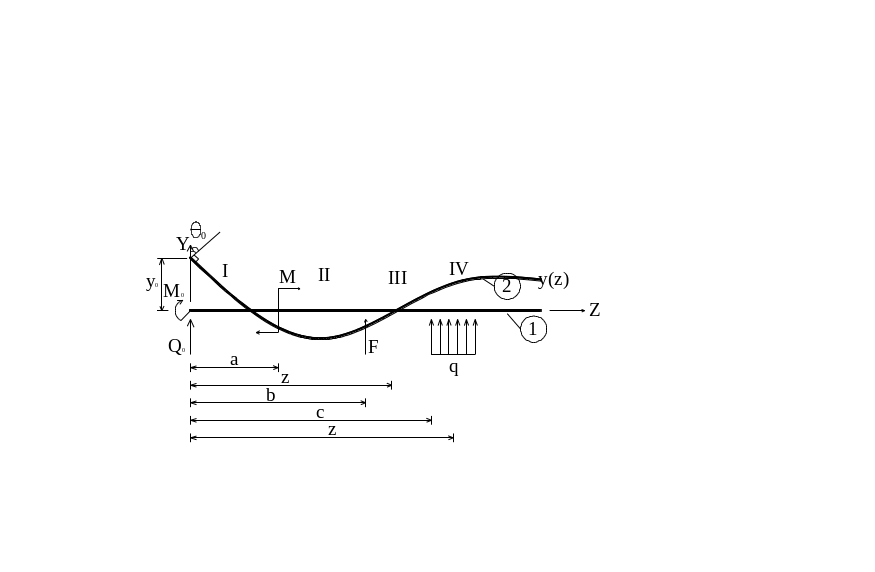
Найдем функцию изгибающего момента на IV участке:
![]() .
.
На III участке:
![]() .
.
Используем приближенное дифференциальное уравнение изгиба:
![]() .
.
Для IV участка:
![]() (1).
(1).
Для III участка:
![]() (2).
(2).
Проинтегрируем дважды выражения (1) и (2):
для IV:
![]()
![]()
![]() (3);
(3);
для III:
![]() (4);
(4);
для IV:
![]()
![]() (5);
(5);
для III:
![]() (6).
(6).
Для того чтобы
упругая линия балки была правильной
кривизны необходимо, чтобы выражения
попарно (3) и (4); (5) и (6) численно совпадали
на границе III
и IV
участков, т.е. при z=c:
![]()
![]() .
.
И вообще:
![]()
![]() (7).
(7).
Определим обе
константы из граничных условий первого
участка:
![]()
![]() .
.
При z=0
имеем:
![]()
![]() (8).
(8).
C
и D
имеют смысл угла поворота в начале
координат (C)
и прогиба в начале координат (D).
![]() и
и
![]() называют начальными параметрами.
Подставляем (8) в уравнение (5) и, обобщая
формулу для любого количества внешних
сил и их направлений, получаем уравнение
начальных параметров.
называют начальными параметрами.
Подставляем (8) в уравнение (5) и, обобщая
формулу для любого количества внешних
сил и их направлений, получаем уравнение
начальных параметров.
![]()
![]() (9),
(9),
где z – абсцисса точки, где отыскивают перемещения,
![]() ,
,![]() - абсциссы точек приложения i-ого
сосредоточенного момента и к-ой
сосредоточенной силы соответственно,
- абсциссы точек приложения i-ого
сосредоточенного момента и к-ой
сосредоточенной силы соответственно,
![]() - абсцисса начала
действия распределенной нагрузки.
- абсцисса начала
действия распределенной нагрузки.
Знак «+» в уравнении (9) принимают в том случае, если данный силовой фактор сообщает точкам оси балки положительные перемещения.
Пример:
Для заделки
![]()
![]()
![]()
![]()
![]() .
.
Частные случаи определения начальных параметров.
Если начало отсчета расположено в заделке, то
 .
.Если начало отсчета – шарнирная опора, то
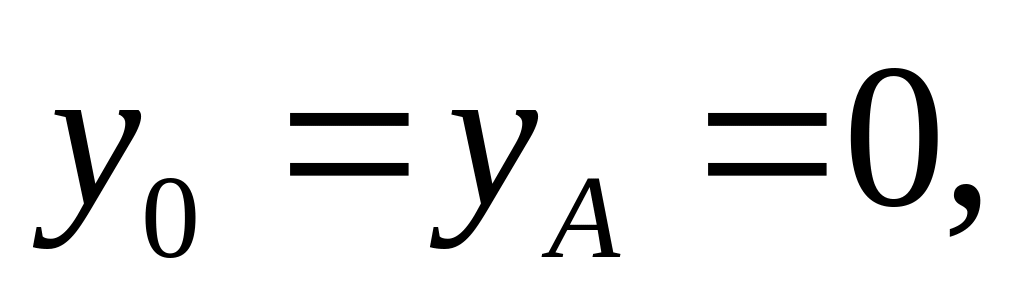
 .
.
Для определения
угла поворота в начале отсчета необходимо
составить уравнение начальных параметров
для точки B,
где
![]() =0:
=0:
![]()
![]()
![]() .
.
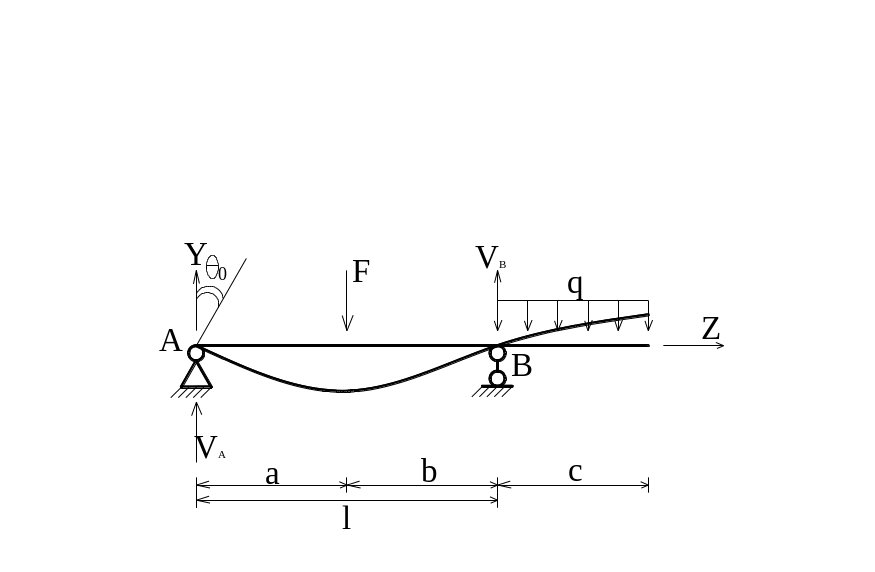
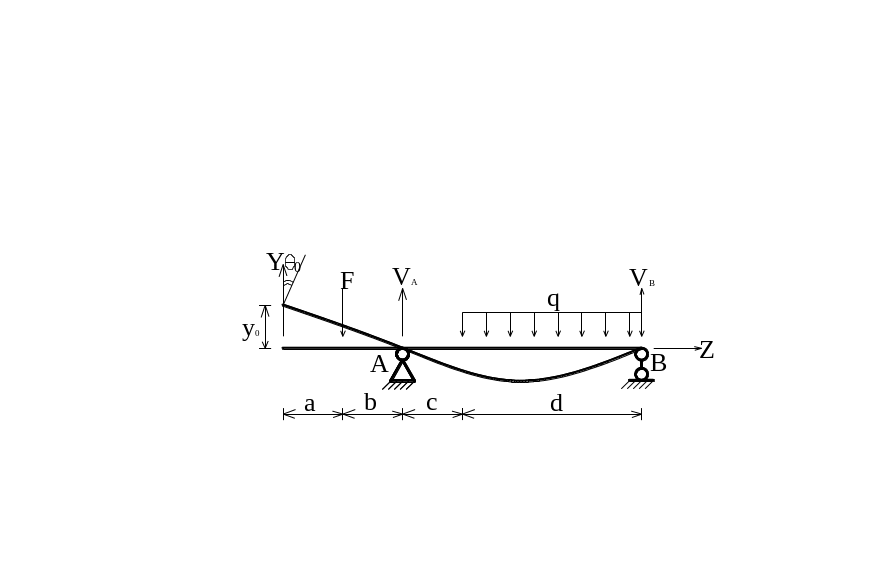
Начало отсчета на свободном конце левой консоли.
Составить выражения
для прогиба и угла поворота не возможно.
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]() .
.
=5=
Балки равного сопротивления
До сих пор мы рассматривали расчет на изгиб стержней, сечение которых оставалось постоянным по длине. Такие стержни, особенно при значительной их длине, нельзя считать рациональными с точки зрения веса и расхода материала, так как размеры сечения подбираются по усилиям, действующим в опасном сечении, в остальных же сечениях получается весьма значительный избыток прочности. Для экономии материала, а также для увеличения в нужных случаях гибкости балок применяют балки равного сопротивления, у которых во всех сечениях наибольшее нормальное напряжение одинаково и не превышает допускаемого значения. Условие, определяющее форму такой балки, получим из условия прочности:
![]() отсюда
можем записать
отсюда
можем записать
![]()
То есть у балки равного сопротивления момент сопротивления данного сечения должен быть прямо пропорционален изгибающему моменту в этом сечении.
В большинстве случаев закон изменения сечения балки равного сопротивления имеет лишь теоретическое значение. Однако он служит той идеальной моделью, на которую в случае необходимости может ориентироваться инженер при реальном конструировании.

=8=
