22. Внутреннее трение в газе

Явление внутреннего трения (вязкости) связано с возникновением сил трения между слоями газа или жидкости, перемещающимися параллельно друг другу с различными по величине скоростями. Со сто­роны слоя, движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила. Наоборот, медленно перемещающийся слой тормозит более быстро движущиеся слои газа. Силы трения, которые при этом возникают, направлены по касательной к поверх­ности соприкосновения слоев. С точки зрения кинетической теории газов, причиной внутреннего трения является наложение упорядо­ченного движения слоев газа с различными скоростями v и хаотичес­кого теплового движения молекул, интенсивность которого зависит от температуры.

Б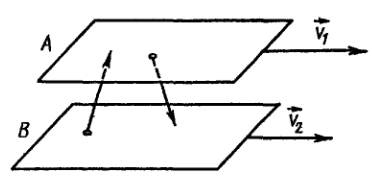 лагодаря тепловому движению молекулы переходят из слоя В (рис. 1), движущегося со скоростью v₂, в слой А движу­щийся со скоростью v₁. При этом молекулы из слоя В «переносят» в слой А импульсы mv₂ своего упорядоченного движения. Если v₁>v₂, то такие молекулы при столкновениях с частицами слоя А ускоряют свое упорядоченное движение, а молекулы слоя А — замедляют. Наоборот, при переходе молекул из быстрее движущегося слоя А в слой В они перекосят большие импульсы mv₁, и соударения между мо­лекулами приводят к ускорению упорядоченного движения молекул слоя В.

η=рD, где D=1/3<V><λ> - коэффициент диффузии.

λ/η_СР=1.

Формулы для коэф. λ, D и η связывают коэф. переноса и характеристики теплового движения молекул.

23. Диффузия в газе.

Диффузия – процесс, заключающийся в самопроизвольном (за счет теплового движения) взаимном проникновении и перемешивании частиц двух соприкасающихся газов, жидкостей и даже твердых тел. Если один газ диффундирует в другой, то процесс называется взаимодиффузией. Самодиффузия – проникновение одной части частиц газа в другую часть того же газа, например при различной концентрации частиц в различных частях объема. Процесс самодиффузии аналогичен процессам переноса (теплопроводности, внутреннего трения) и отличается от них только величиной, которая переносится.

Р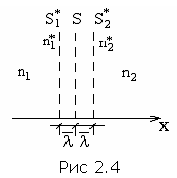 ассмотрим диффузию на следующей модели. Пусть объем с газом характеризуется тем, что плотность газа (концентрация) в нем в направлении «х» изменяется. Получим суммарный поток газа через сечение S как разницу потоков от S₁* к S и от S₂* к S. Пусть n₁* > n₂* .

.

Величину 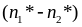выразим через градиент концентрации

Тогда выражение для можно записать в виде 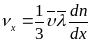. Сравнивая (16) с законом Фика для самодиффузии , видим, что коэффициент самодиффузии связан с микропараметрами газа выражением .

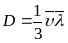19. Максвелловское распределения молекул газа по скоростям.

1. При выводе основного уравнения кинетической теории газов мы считали, что молекулы имеют различные скорости. Опыт под­тверждает это предположение. Средняя квадратичная скорость, исполь­зованная нами ранее, является одной из характеристик движения всей совокупности молекул. Она, разумеется, не имеет смыс­ла применительно к одной какой-либо молекуле или к неболь­шому числу молекул.

2. Д. К Максвелл теоретически решил задачу о распределении молекул идеального газа по скоростям поступательного движения. Он установил закон, позволяющий определить, какое число молекул dn из общего количества n₀ молекул идеального газа в единице объема обладает при данной температуре скоростями, лежащими в интервале от u до u+Δи. При этом Д. К. Максвелл предполагал, что газ хими­чески однороден и находится в состоянии термодинамического рав­новесия.

Закон распределения молекул по скоростям имеет следующий вид:

где m — масса молекулы, k — постоянная Больцмана, Т — абсолют­ная температура. Из этой формулы можно определить так называемую наиболее вероятную скорость молекул и_В соответствующую максимуму выражения dn/du:

где 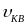— средняя квадратичная скорость. Таким образом, наиболее вероятная скорость молекул зависит только от температуры газа и его молярной массы.

Закон максвелловского распределения молекул по скоростям мо­жет быть записан также в виде:

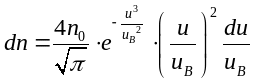
На рис. приведем кривая закона распределения молекул по скоростям