9. Колебательные движения материальной точки.

Колебательным движением, или просто колебаниями, называют всякое движение или изменение состояния, характеризуемое той или иной степенью повторяемости во времени значений физических величин, определяющих это движение или состояние. Приме­рами колебательного движения в механике могут служить колебания маятников, струн, мембран телефонов, балансиров карманных часов, поршней двигателей внутреннего сгорания, мостов и других сооруже­ний, подвергающихся переменной нагрузке, и т. д.

Колебательное движение называют периодическим, если значения физических величин, изменяющихся в процессе колебаний, повто­ряются через равные промежутки времени Простейшим типом периодических колебаний являются так называемые гармонические колебания. Колебания какой-либо физической величины х называют­ся гармоническими, если ее зависимость от времени t имеет вид

или 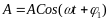, где А – амплитуда колебаний т.е. максимальное отклонение от точки колебаний, 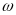- круговая частота, и 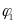- начальные фазы (В зависимости от начальной фазы берем то или иное уравнение).

Е сли колеблется материальная точка, то это поступательное движение.

F=ma

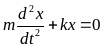
_{Колебание материальной точки под действием упругих сил. Решение этого дифф. уравнения второго порядка можно записать в виде гармонической функции}

12. Законы сохранения в механике мт.

Закон сохранения и превращения механической энергии: в замкнутой системе сил полная механическая энергия сохраняется т.е. не изменяется со временем. Это фундаментальный закон природы, он является следствием однородности времени – инвариантности физических законов относительно выбора начала отсчета времени. Или звучит так: в замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела к другому, но ее общее количество остается неизменным.

_{Для упругого:}

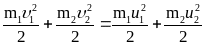
_{Абсолютно неупругого и частично неупругого:}

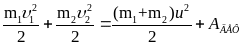
Закон сохранения импульса:

Механическую систему называют замкнутой, или изолированной, если на нее не действуют внешние силы, т. е. если она не взаимодействует с внешними телами. 2. Для замкнутой системы главный вектор внешних сил тождест­венно равен нулю. Поэтому вытекает следующий закон, на­зываемый законом сохранения импульса: импульс замкнутой системы не изменяется с течением времени, т. е. dP/dt=0 и ,

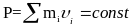где m_i и v_i— масса и скорость i-ой материальной точки системы, а n — общее число материальных точек, входящих в состав системы.

13. Условия равновесного состояния тел.

1. Равнодействующая всех сил равна нулю

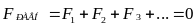
При вычислении равнодействующей всех сил действующих на тело можно прикладывать к центру масс.

2. Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если векторная сумма моментов всех приложенных к нему сил относительно этой оси равно нулю.

Виды равновесий: безразличное, устойчивое неустойчивое.

14. Параметры и основной закон вращательного движения.

Вращательное движение характеризуется следующими параметрами:

Момент инерции (мера инертных свойств вращающегося тела) 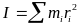. момент инерции тела зависит от формы тела, относительно какой оси вращается тело и от распределения массы по объему тела.

Угловая скорость

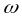
Угловое ускорение

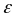
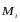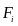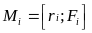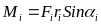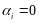Момент силы относительно заданной оси вращения: или . Следовательно при и 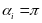момент силы равен нулю. (r_i - радиус-вектор МТ). Если внешние силы приложены к нескольким точкам тела, то результирующий или полный момент относительно оси вращения равен алгебраической сумме моментов каждой из сил относительно той же оси. Что касается полного момента всех внутренних сил (сил взаимодействия между всеми парами частиц) относительно оси вращения, то по третьему закону Ньютону он равен нулю.

Момент импульса применительно к –ой МТ, линейная скорость которой 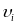момент импульса определяется как 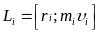Величина полного момента импульса тела равна арифметической сумме моментов импульсов всех его точек, так как при вращении тела все его точки вращаются в одном и том же направлении.

Основной закон: 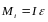или где - полный момент внешних сил относительно оси вращения.