
- •1. Параметры и закономерности прямолинейного движения мт.
- •2. Криволинейное движение материальной точки.
- •3. Основные законы поступательного движения
- •4. Принципы суперпозиций и относительность движение мт.
- •1. Принцип относительности Галилея
- •5. Работа и энергия и их эквивалентность.
- •9. Колебательные движения материальной точки.
- •12. Законы сохранения в механике мт.
- •13. Условия равновесного состояния тел.
- •14. Параметры и основной закон вращательного движения.
- •15. Методика определения момента инерции тела (на примере точки). Теорема Штейнера.
- •16. Закон сохранения для вращательного движения.
- •17. Колебательное движение твердого тела, определение частоты колебаний.
- •18. Степени свободы механического движения системы тел. Закон равнораспределения энергии для газа.
- •21. Теплопроводность газа.
- •22. Внутреннее трение в газе
- •23. Диффузия в газе.
- •19. Максвелловское распределения молекул газа по скоростям.
- •24. Закон сохранения энергии для изотермического и адиабатического.
- •27. Термодинамические циклы, кпд тепловых машин.
- •25. Работа газа и его теплоемкость при изо- и адиабатных процессах.
- •26. Уравнение Пуасона, уравнение политропического процесса.
- •29. Молекулярно-кинетический смысл энтропии.
- •20. Больцмановское распределение молекул газа.
- •31. Уравнение состояния газа и его применение.
- •10. Явление резонанса при колебании мт.
1. Параметры и закономерности прямолинейного движения мт.
Положение точки М относительно системы отсчета можно задать не только с помощью трех ее декартовых координат х, у, z, но также с помощью одной векторной величины r — радиуса-вектора точки М, проведенного в эту точку из начала О системы координат. Если i, j и к — единичные векторы (орты) осей прямоугольной декартовой системы координат, то r = xi+yj+zk. Векторы xi, yj и zk представляют собой составляющие (компоненты) радиуса-вектора, г вдоль соответствующих осей координат. При движении материальной точки М ее координаты х, у, z и радиус-вектор r изменяются с течением времени t. Поэтому для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени: х = х(t), y = y(t) и z = z(t) (1.1), либо зависимость от времени радиуса-вектора этой точки r = r(t) (1.2). Три скалярные уравнения (1,1) или эквивалентное им одно векторное уравнение (1,2) называют кинематическими уравнениями движения МТ. 1. Траекторией МТ называют линию, описываемую в пространстве этой точкой при ее движении. Уравнения движения (1.1) задают траекторию точки в так называемой параметрической форме. Роль параметра играет время t. В зависимости от формы траектории различают прямолинейное и криволинейное движения точки. Если все участки траектории точки лежат в одной плоскости, то движение точки называют плоским.
2. Длиной пути s материальной точки называют сумму длин всех участков траектории, пройденных точкой за рассматриваемый промежуток времени. Очевидно, что длина пути s не может быть отрицательной.
3. Вектором перемещения материальной точки за время от t1 ао t2 называют вектор, проведенный из положения этой точки в момент t1 в ее положение в момент t2, т. е. приращение радиуса-вектора точки за рассматриваемый промежуток времени: r2-r1= r(t2)- r(t1). Из того что перемещение — вектор, следует подтверждающийся на опыте закон независимости движений: если точка одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею за то же время в каждом из движений порознь.
4.
Для характеристики движения материальной
точки вводят векторную физическую
величину — скорость,
определяющую как быстроту движения,
так и направление движения в данный
момент времени. Вектором средней скорости
vcp
точки в интервале времени от t
до
 называют
отношение приращения
называют
отношение приращения
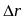 радиуса-вектора точки за этот интервал
времени к его величине
радиуса-вектора точки за этот интервал
времени к его величине
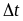 :
:
 (1.3).
Вектор vcp
направлен
так же, как
.
Если
в выражении (1.3) перейти к пределу,
устремляя
к нулю, то мы получим выражение для
скорости (ее часто называют мгновенной
скоростью)
материальной точки t
момент прохождения ее через точку М
траектории:
(1.3).
Вектор vcp
направлен
так же, как
.
Если
в выражении (1.3) перейти к пределу,
устремляя
к нулю, то мы получим выражение для
скорости (ее часто называют мгновенной
скоростью)
материальной точки t
момент прохождения ее через точку М
траектории:
 .
5.
Для характеристики быстроты изменения
скорости движения вводится понятие
ускорения.
Средние ускорение
.
5.
Для характеристики быстроты изменения
скорости движения вводится понятие
ускорения.
Средние ускорение
 .
Ускорение
или мгновенное ускорение
-
.
Ускорение
или мгновенное ускорение
-
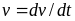 .
.
6.
В случае равномерного прямолинейного
движения материальной точки вдоль
положительного направления оси ОХ
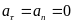 и
и
 ,
причем
,
причем
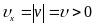 .
Зависимость координаты х
точки
от времени t
имеет вид:
.
Зависимость координаты х
точки
от времени t
имеет вид:
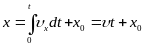 ,
где
Х0—
значение х
в
момент начала отсчета времени. Длина
пути s,
пройденного
точкой за промежуток времени от 0
до t,
s=x-x0=vt.
,
где
Х0—
значение х
в
момент начала отсчета времени. Длина
пути s,
пройденного
точкой за промежуток времени от 0
до t,
s=x-x0=vt.
7.
В качестве второго примера прямолинейного
движения материальной точки рассмотрим
равнопеременное прямолинейное движение.
В этом случае аn=0
и аt=const.
Если аt>0,
то движение называют равноускоренным,
а если аt<0
— равнозамедленным.
Так как аt=dv/dt,
то
зависимость численного значения скорости
точки от времени имеет вид ,где
v0—
начальная скорость, т. е. скорость
материальной точки в
момент
t
=
0.
Если движение происходит вдоль
положительного направления оси ОХ,
то
,где
v0—
начальная скорость, т. е. скорость
материальной точки в
момент
t
=
0.
Если движение происходит вдоль
положительного направления оси ОХ,
то
 и
координата х
материальной
точки зависит от t
по следующему закону:
и
координата х
материальной
точки зависит от t
по следующему закону:
 ,
где
х0—
значение х
при
t=0.
,
где
х0—
значение х
при
t=0.
