4 Законы регулирования

Законом регулирования называют мат. зависимость в соотношении с которым управление воздействия вырабат-сь безинерционным УУ.

Закон 1. Пропорциональный. M=k*x(t) – ход пропорционален входу.

y(t) = k*x(t). Велечину k называют коэффициентом передачи регулятора. Обратную велечину (1/к) –статизмом регулятора. Закон используется для построения регуляторов. По такому закону работают усилители. Его называют безинерционным законом.

Закон 2. Интегральный. , . Интегральный регулятор обеспечивает астатическое регулирование. При интегральном законе уравнение воз-е в каждой момент времени пропорционально сигналу ошибки, это означает что уровень воздействия на объект определяется суммарной ошибкой системы.

Закон 3. Пропорционально интегрированный(является комбинацией двух предыдущих). . Благодаря наличию интегральной составляющей обеспечивает неплохую точность в установившихся режимах. А при определенном сочетании коэффициентов обеих законах обеспечивает хорошие показатели в переходных режимах.

Закон 4. Пропорциональный дифференциальный интегральный . Пид закон очень часто используется в системах прямой сетки.

5 Динамическая и статическая математическая модель системы. Линеаризация.

Статические модели описывают установившиеся режимы работы, когда сигналы и регулируемые величины остаются постоянными, неизменными. Для описания статики обычно используются алгебраические уравнения.  Динамические модели описывают переходные режимы работы. Они могут представляться в различных видах:  1) системы дифференциальных или операторных уравнений первого порядка;  1) одним дифференциальным или операторным уравнением более высокого порядка;  2) передаточными функциями;  3) структурными схемами;  4) матричное описание в пространстве состояний и др.  Для описания объектов, работающих при случайных воздействиях, используются вероятностные (стохастические) модели.  Из динамических моделей легко получить статические. Достаточно положить производные (или оператор Лапласа) равными нулю.

Линеаризация статических характеристик

Статическая характеристика - связывает входную величину с выходной звена, когда все остальные величины постоянны (при установившихся внутренних процессах): Y = F(X);

Линеаризация проводится, если в окрестности некоторой рабочей точки (х₀,y₀) линеаризованная функция непрерывна:

если члены старших порядков отбросить, то получаем:

или

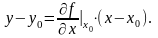
Отсюда: ; ; ; ; .

Линеаризация проводится с погрешностью! обязательно в окрестности некоторой (рабочей) точки.

Динамические характеристики звена

Позволяют описать поведение звена (системы) во времени. Разделяются на дифференциальные и разностные уравнения. Для случая многомерного звена данные уравнения связывают входные и выходные переменные и их производные (сколь угодно большого порядка). Данные математические модели могут быть как в виде одного уравнения, так и в виде систем уравнений. В одномерном случае имеет место связь между одной входной и одной выходной переменными и их производными:

.

Применяя формулу Тейлора и отбрасывая старшие производные (2-й степени и выше) получаем:

,

или линейное уравнение с постоянными коэффициентами, с учетом того, что

:

.

Такое уравнение описывает поведение звена только в окрестности некоторой точки .

При значительном удалении от точки линеаризации данное уравнение как правило несправедливо. Полученное уравнение также называется уравнением в отклонениях или уравнением вариации. Практически и заменяют на x и y. Тогда окончательно имеем дифференциальное уравнение:

,

или в операторной форме .

Откуда получается : .

Можно обозначить Q(p) = - собственный полином,

R(p) = - входной полином.

При наличии возмущений уравнение, описывающее звено, усложняется:

,

а в операторной форме:

, или

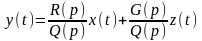, где - полином возмущения.

Полученные уравнения носят названия уравнения вход-выход.

ЛИНЕАРИЗАЦИЯ

Как правило, системы описываются не линейными дифференциальными уравнениями. В системах управления поддерживается заданный режим. При этом решения входные и выходные велечины изменяются по определнному закону. Из различных возмущающих фактов , фактический режим отличается от заданного. Это отклонение достаточно мало, что позволяет произвести линеаризацию, разлогая уравнение в ряд Тейлора. Линеаризацию можно производить по отдельным звеньям системы.

Пример. Пусть звено описывается дифуравнением F(y,y`,y``,u,u`)+f=0 и пусть заданному компоненту решение: y=y*, y`=y`*, y``=y``*, u=u*, u`=u`*, f=f*.

Δu=u*

Δy=y-y*

Δ`y=y`-y`*

Δy``=y``-y``*

Δu`=u`-y(u)*

Δ f= u-u*

Поставим эти значения в уравнение 2, а затем разложем эту функцию в ряд тейлора по откланению в точке рабочего режима.

Разложение в ряд Тейлора.:

F*+(df/dy)* * Δy+(df/dy`)* * Δy`+(df/du)* * Δu +f(df/du`)** Δuf(df/du`)* Δu`+ Δf*+ Δf=0

Члены более высоких порядков были отброшены, так как отклонение фактического от номинального мало. Функция f для осущесвления этого разложения должна обладать частным производным по всем аргументам в окресности точки соответствующего рабочего режима

6 Преобразование Лапласа. Свойства преобразования Лапласа.

Рассмотрим функцию f (t) вещественной переменной (t), отвечающую следующим условиям:

(t) непрерывна для всех значений ³ 0, допускается конечное число точек разрыва непрерывности первого рода

(t) при t < 0

3) f (t) имеет ограниченный порядок возрастания, т.е. можно указать такие постоян­ные числа 0 и С0 ³ 0, при которых выполняется неравенство

,  где число С0 является показателем роста функции

Функция f (t), удовлетворяющая условиям (1) - (3), называется оригиналом.

Пример: 1(t), 1(t)Asinwt, eat 1(t), t n 1(t). Изображением функции f (t) по Лапласу называется функция F(S) комплексного переменного S=с+jw, определяемая равенством

, (2.14)  где L - оператор Лапласа.

Рассмотрим основные свойства преобразования Лапласа.

1. Свойство линейности:

. (2.15)

2. Дифференцирование оригинала:

, (2.16)

, (2.17)

Если начальные условия нулевые, т.е.

,

то последняя формула принимает вид

,  т.е. дифференцированию f(t) соответствует умножение изображения F(S) на S.

3. Интегрирование оригинала:

. (2.18)

При нулевых начальных условиях интегрирование оригинала сводится к делению изображения на S:

. (2.19)

Свойства 3 и 2 позволяют дифференциальные и интегральные уравнения преобра­зовать в алгебраические, что существенно упрощает исследование САУ.

4. Теорема запаздывания. Для любого положительного числа t

. (2.20)

5. Теорема о свертке (теорема умножения изображений)

Если f1(t) и f2(t) - оригиналы, а F1(S) и F2(S) - их изображения, то

. (2.21)

Интеграл правой части­ называют сверткой функции f1(t) и f(t) и обозначают f1(t)*f2(t).

6. Теорема о предельных значениях.

Если f(t) оригинал, а F(S) - его изображение, то

 , и при существовании предела ,

7 Передаточная функция. Формы записи передаточных функций.