Цилиндрической поверхностью называется поверхность (рис. 18), образованная прямыми (образующими), параллельными некоторой данной прямой L и пересекающими данную линию С (направляющую).

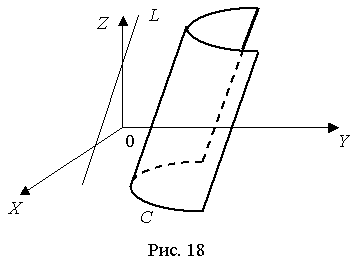
Допустим, что направляющая С задана уравнениями

а образующая L задана уравнениями

где X, Y, Z - текущие координаты точек, принадлежащих образующим, т.е. цилиндрической поверхности;  x, y, z - координаты точек, принадлежащих направляющей С.

Если из уравнений (53) и (54) исключим x, y, z, то получим уравнение относительно переменных X, Y, Z, т.е. уравнение цилиндрической поверхности.

Заметим, что всякое уравнение вида

не содержащее координаты z, определяет цилиндрическую поверхность с образующей, параллельной оси Oz.

На координатной плоскости Oxy уравнение (55) определяет плоскую линию, которую обычно называют направляющей рассматриваемой цилиндрической поверхности. В пространстве эта линия определяется двумя уравнениями F(x, y) = 0 и z = 0.

Рассмотрим уравнения известных кривых второго порядка:

и примем их за уравнения направляющих цилиндрических поверхностей.

Тогда в пространстве эти уравнения будут представлять следующие цилиндрические поверхности:

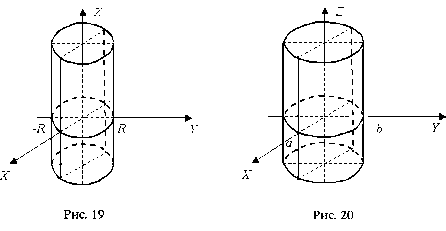
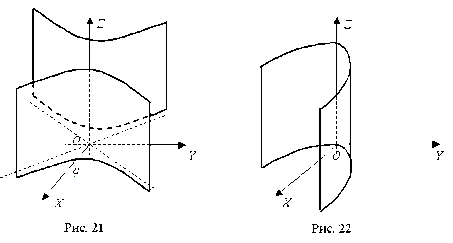
уравнение (56) - прямой круговой цилиндр (рис. 19),  уравнение (57) - эллиптический цилиндр (рис. 20),  уравнение (58) - гиперболический цилиндр (рис. 21),  уравнение (59) - параболический цилиндр (рис. 22). 

Конической поверхностью называется поверхность (рис. 23), образованная прямыми (образующими конуса), проходящими через данную точку (вершину конуса) и пересекающими данную линию (направляющую конуса).

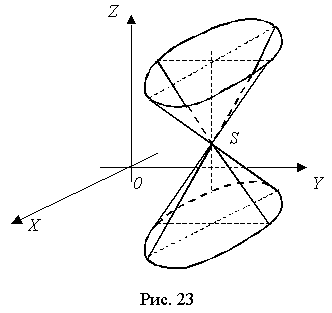
Пусть направляющая конуса задана уравнениями:

а вершина S конуса имеет координаты x₀, y₀, z₀.

Уравнения образующей запишем как уравнения прямой, проходящей через две точки S(x₀, y₀, z₀) и M(x, y, z), принадлежащие направляющей (60):

где X ,Y, Z - текущие координаты точек образующих.

Исключая из уравнений (60) и (61) x, y, z, получим уравнение относительно переменных X, Y, Z, т.е. уравнение конической поверхности.

Поверхностью вращения называется поверхность, образованная вращением какой-либо плоской линии вокруг прямой, лежащей в плоскости этой линии.

Для вывода уравнения поверхности вращения необходимо выбрать систему координат. Чтобы уравнение поверхности вращения выглядело проще, ось вращения принимают за одну из координатных осей.

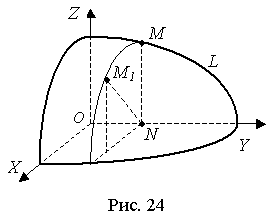
Пусть в координатной плоскости Oyz задана кривая L уравнением F(Y, Z)=0 (рис. 24). Вращаем кривую L вокруг оси Oy. Получим некоторую поверхность. Пусть M(x, y, z) - произвольная точка получившейся поверхности. Тогда     , но   т.к. если взять точку M₁ с отрицательной аппликатой, то

Следовательно, имеем Y = y,   и координаты точки M(x, y, z) удовлетворяют уравнению

Уравнение (62) и есть искомое уравнение поверхности вращения.

Т. о., чтобы получить уравнение поверхности, образованной вращением линии L, лежащей в плоскости Oyz, вокруг оси Oy, нужно в уравнении этой линии заменить z на 

Аналогичные правила будут иметь место и по отношению к уравнениям поверхностей, полученных вращением плоских линий вокруг других координатных осей.

Линейное, или векторное пространство   над полем P — это непустое множество L, на котором введены операции

сложения, то есть каждой паре элементов множества   ставится в соответствие элемент того же множества, обозначаемый   и

умножения на скаляр (то есть элемент поля P), то есть любому элементу   и любому элементу   ставится в соответствие единственный элемент из  , обозначаемый  .

При этом на операции накладываются следующие условия:

, для любых   (коммутативность сложения);

, для любых   (ассоциативность сложения);

существует такой элемент  , что   для любого   (существование нейтрального элемента относительно сложения), в частности L не пусто;

для любого   существует такой элемент  , что   (существование противоположного элемента относительно сложения).

 (ассоциативность умножения на скаляр);

 (унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).

 (дистрибутивность умножения на вектор относительно сложения скаляров);

(дистрибутивность умножения на скаляр относительно сложения векторов).

Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.

Простейшие свойства

Векторное пространство является абелевой группой по сложению.

Нейтральный элемент   является единственным, что вытекает из групповых свойств.

 для любого  .

Для любого   противоположный элемент   является единственным, что вытекает из групповых свойств.

 для любого  .

 для любых   и  .

 для любого  .

Связанные определения и свойства

Подпространство

Алгебраическое определение: Линейное подпространство или векторное подпространство ― непустое подмножество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как Lat(L). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы

;

для всякого вектора  , вектор   также принадлежал K, при любом  ;

для всяких векторов  , вектор   также принадлежал K.

Последние два утверждения эквивалентны следующему:

для всяких векторов  , вектор   также принадлежал K для любых  .

В частности, пространство, состоящее из одного элемента {θ}, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными.

Свойства подпространств

Пересечение любого семейства подпространств — снова подпространство;

Сумма конечного семейства подпространств — снова подпространство. Сумма подпространств   определяется как множество, содержащее всевозможные суммы элементов K_i:

.

В функциональном анализе в бесконечномерных пространствах особо выделяют замкнутые подпространства.

Базис. Размерность

Конечная сумма вида

называется линейной комбинацией элементов   с коэффициентами  .

Линейная комбинация называется нетривиальной, если хотя бы один из её коэффициентов отличен от нуля.

Элементы   называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулевому элементу θ. В противном случае эти элементы называются линейно независимыми.

Бесконечное подмножество векторов из L называется линейно зависимым, если линейно зависимо его некоторое конечное подмножество, и линейно независимым, если любое его конечное подмножество линейно независимо.

Число элементов (мощность) максимального линейно независимого подмножества пространства не зависит от выбора этого подмножества и называется рангом, или размерностью, пространства, а само это подмножество — базисом (базисом Га́меля или линейным базисом). Элементы базиса также называют базисными векторами. Свойства базиса:

Любые n линейно независимых элементов n-мерного пространства образуют базис этого пространства.

Любой вектор   можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов:

.

Линейная оболочка

Линейная оболочка   подмножества X линейного пространства L — пересечение всех подпространств L, содержащих X.

Линейная оболочка является подпространством L.

Линейная оболочка также называется подпространством, порожденным X. Говорят также, что линейная оболочка   натянута на множество X.

Линейная оболочка   состоит из всевозможных линейных комбинаций различных конечных подсистем элементов из X. В частности, если X — конечное множество, то   состоит из всех линейных комбинаций элементов X.

Если X — линейно независимое множество, то оно является базисом   и тем самым определяет его размерность.

Примеры

Нулевое пространство, единственным элементом которого является ноль.

Пространство всех функций   с конечным носителем образует векторное пространство размерности равной мощности X.

поле вещественных чисел может быть рассмотрено как континуально-мерное векторное пространство над полем рациональных чисел.

Любое поле является одномерным пространством над собой.

Координаты вектора линейного пространства

Если система векторов e₁, ..., e_n n-мерного линейного пространства L_n образует базис в L_n, то любой вектор x из L_n может быть представлен в виде

x = С₁·e₁+ С₂·e₂+ ...+ С_n· e_n.

Выражение x = С₁·e₁+ С₂·e₂+ ...+ С_n· e_n называется разложением вектора по базису e₁, ..., e_n, а числа С₁, С₂, ..., С_n называются координатами вектора x  в базисе e₁, ..., e_n.

Координаты вектора принято обозначать тем же символом, что и сам вектор:

x = x₁·e₁+ x₂·e₂+ ...+ x_n· e_n.

Взаимно однозначное соответствие x = x₁·e₁+ x₂·e₂+ ...+ x_n· e_n ⇐⇒ x = (x₁, x₂, ..., x_n)

— изоморфизм L_n и R_n.

     Базис - любая упорядоченная система   из n линейно независимых векторов пространства  . Обозначение: 

Преобразование координат вектора при преобразовании базиса

Пусть 

^

A

:X_n → X_n — линейный оператор. Зададим в X_n два базиса: "старый" базис e = (e₁, e₂,  … , e_n) и "новый" базис f = (f₁, f₂,  … , f_n) .

Матрицей перехода от базиса e к базису f называется матрица C = (c_ik)    (i,k = 1, … ,n) , столбцами которой являются координатные столбцы векторов f₁, f₂,  … ,f_n в базисе e , т.е.

f₁ = c₁₁ e₁ + c₂₁ e₂ + … + c_n1 e_n, f₂ = c₁₂ e₁ + c₂₂ e₂ + … + c_n2 e_n, … … … … … …  , f_n = c_1n e₁ + c_2n e₂ + … + c_nne_n,

или в матричной форме:

f = eC

(1)

где C — матрица перехода

C =	     	c11 c12 … c1n c21 c22 … c2n … … … … cn1 cn2 … cnn	     

Замечание. В силу линейной независимости базисных векторов матрица C — невырожденная ( det C ≠ 0 ). Следовательно, C имеет обратную матрицу C ^{− 1} .

Теорема 1. Преобразование координат вектора при переходе от "старого" базиса e к "новому" базису f определяется формулой:

X\f = C − 1X\e.

(2)

Доказательство. Обозначим координатные столбцы произвольного вектора x  X_n в "старом" базисе e

Xe =	     	x1 x2 … xn	     

и в "новом" базисе f

Xf =	     	x'1 x'2 … x'n	     

Произвольный вектор x в базисе e имеет вид:

x = eXe

(3)

В базисе f тот же вектор имеет вид:

x = fX_f

x = eCXf.

(4)

и в силу формулы (1)

Сравнивая формулы (3) и (4), получаем

X_\e = C · X_f.

Умножая это равенство слева на C ⁻¹ , получаем формулу (2), которую требовалось доказать.