Свойства функций, непрерывных на отрезке
Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое числоC> 0, что x [a, b] выполняется неравенство |f(x)| ≤ C.
Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x [a, b] (рис.2).
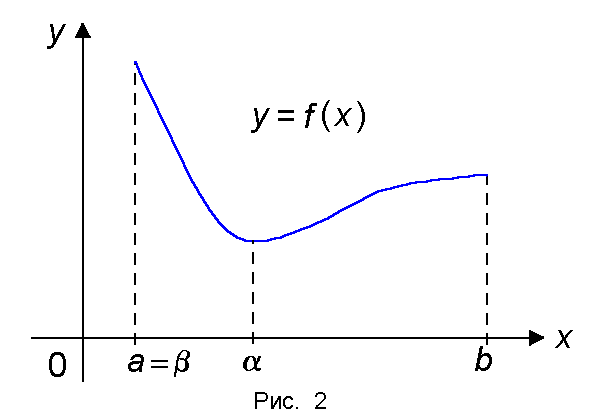
Наибольшее значение M обозначается символом maxx [a, b] f(x), а наименьшее значение m — символом minx [a, b] f(x).
Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a,b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0.
Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX (р
Теорема о существовании и непрерывности обратной функции:
1)
Если функция f монотонна на множестве
X и принимает значения на множестве Y
(
),
то на множестве Y определена обратная
функция, принимающая значения в множестве
X и обладающая тем же характером
монотонности, что и сама функция f.
2) Если X=[a,b] и f монотонна и непрерывна на этом множестве, то множество значений функции f есть [f(a),f(b)] и обратная функция непрерывна на нем.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.
Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f (xо) = 0, либо f (xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
Первое достаточное условие. Пусть xо - критическая точка. Если f (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе
достаточное условие. Пусть
функция f(x)
имеет производную
f (x)
в окрестности точки xо и
вторую производную 
в
самой точке xо.
Если f (xо)
= 0,
>0
(
<0),
то точка xо является
точкой локального минимума (максимума)
функции f(x).
Если же
=0,
то нужно либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
функция f(x) возрастала (убывала) на этом интервале, необходимо и достаточно,
чтобы во всех его точках производная была неотрицательной f′(x) > 0
(неположительной f’(x) < 0)
Непрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x1 и x2 из этого отрезка
|
|
|
|
График 3.2.3.1. Выпуклая вверх функция |
Аналогично определяется функция, выпуклая вниз.
Дважды
дифференцируемая на [a; b] функция
f (x) выпукла вверх, если для любого
|
Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого
|
Так,
вторая производная функции
равна
откуда
следует, что квадратичная функция
выпукла вниз на всей области определения.
Пусть
функция f (x) непрерывна в точке
и
имеет в этой точке конечную или
бесконечную производную. Тогда точка
называется
точкой перегиба функции f, если в этой
точке изменяется направление ее
выпуклости.
Необходимое условие наличия точки перегиба. Если – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то
|
Достаточные условия наличия точки перегиба.
Пусть
функция f (x) непрерывна и имеет
конечную или бесконечную производную
в точке
Если
меняет
знак при переходе через точку
то
–
точка перегиба функции f (x).
Если
то
–
точка перегиба функции f (x).
Функция нескольких перепенных является расширением исчисления функций одной переменной в исчисление функций нескольких переменных: функции, которые дифференцируются и интегрируются, затрагивая несколько переменных, а не одну.
Функция называется непрерывной в точке M0(x0y0), если
Справедливо и обратное утверждение: если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции, то функция непрерывна
Частные приращения и частные производные
О:
Под частным приращением функции
по
понимается
разность
,
под частным приращением по
подразумевается
.
О:
Частная производная по
-
это предел отношения частного приращения
к
приращению
,
если
предполагает
стремление к нулю:
.
Геометрический смысл частных производных:
Рассмотрим функцию двух переменных f(x, y) , определенную в некоторой окрестности точки (x0, y0) . Пусть она имеет в этой точке частную производную
f'x(x0, y0) =
f(x, y0) |
|
x = x0 = tg α. |
||
|
|
Согласно геометрическому смыслу производной функции одной переменной f(x, y0) , α является углом между осью OX и касательной к графику этой функции, т.е. к кривой, определяемой системой уравнений
|
|
|
|
||
|
|
в точке (x0, y0, z0) , где z0 = f(x0, y0)
производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.
Производную по направлению дифференциируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
,
де
—
орт направления. Отсюда следует, что
максимальное значение в точке производная
по направлению принимает, если направление
совпадает с направлением градиента
функции в данной точке. Также видно,
что значение производной по направлению
не зависит от длины вектора
.
Свойства градиента и производной по направлению
для
скалярного произведения
двух
векторов
и
выполняется
равенство
где
--
угол между векторами
и
.
Записав это равенство для векторов
и
,
получим, что
где
--
угол между осью
и
вектором
,
поскольку
.
Учитывая, что
,
получаем:
Экстремум функции двух переменных
Пусть
функция
определена в некоторой области G и точка
.
Функция
имеет в точке
максимум,
если существует такая окрестность этой
точки, что для всех точек
этой окрестности, отличных от
,
выполняется неравенство
.
Аналогично определяется минимум функции.
Максимум и минимум функции называются экстремумами функции.
Теорема
(необходимое условие экстремума). Если
–точка
экстремума функции
,
то частные
производные
и
в этой точке
равны нулю или не существуют.
Точки,
в которых частные производные
и
обращаются в нуль или не существуют,
называются критическими
точками этой функции.
Сформулированный признак не является достаточным: не обязательно критическая точка является точкой экстремума.
Чтобы проверить, есть ли экстремум в критической точке, используют следующую теорему (достаточное условие экстремума).
Пусть
в некоторой области, содержащей точку
,
функция
имеет
непрерывные частные производные до
3–го порядка включительно и
.
Обозначим:
.
Тогда
1)если
,
то функция
имеет экстремум
в точке
,
причем это максимум, если
и минимум,
если
;
2)если
,
то экстремума
в точке
нет;
3)если
,
требуется
дополнительное исследование (экстремум
в точке
может быть или не быть).
Необходимое условие локального экстремума дифференцируемой функции
Если
-
точка экстремума функции f,
то
и
или
Достаточные условия локального экстремума дважды дифференцируемой функции
Обозначим
Если D > 0, A > 0, то - точка минимума.
Если D > 0, A < 0, то - точка максимума.
Если D < 0, экстемума в точке нет.
Если D = 0, необходимы дополнительные исследования.