Кулабухов С.Ю. Дискретная математика

x 1. pOSTROENIE ALGEBRY WYSKAZYWANIJ

13.rAWNOSILXNY LI FORMULY ZADANIQ 5?

14.nE PRIBEGAQ K ZAPISQM DOKAVITE ZAKONY LOGIKI 1{4, 6, 8{10.

15.sKOLXKO SU]ESTWUET POPARNO NERAWNOSILXNYH FORMUL OT ODNOJ WYSKAZYWATELXNOJ PERE- MENNOJ. oT DWUH WYSKAZYWATELXNYH PEREMENNYH?

1.11.uPRAVNENIQ.

1.oBOZNA^IW PROSTYE WYSKAZYWANIQ BOLX[IMI LATINSKIMI BUKWAMI, A LOGI^ESKIE SWQZKI SOOTWETSTWU@]IMI SIMWOLAMI, ZAPISATX W WIDE FORMUL SLEDU@]IE WYSKAZYWANIQ:

\ESLI DIAGONALI PARALLELOGRAMMA WZAIMNO PERPENDIKULQRNY ILI QWLQ@TSQ BISSEKTRISAMI UGLOW, TO \TOT PARALLELOGRAMM ESTX ROMB"

\ESLI PRI PERESE^ENII DWUH PRQMYH TRETXEJ, WNUTRENNIE NAKRESTLEVA]IE UGLY RAWNY, TO \TI PRQMYE PARALLELXNY"

\ESLI CELOE ^ISLO POLOVITELXNO I QWLQETSQ ^ETNYM, TO LIBO ONO PROSTOE LIBO BOLX[E DWUH"

2.pUSTX BUKWY A, B, C, D OBOZNA^A@T WYSKAZYWANIQ: A | \\TO ^ISLO QWLQETSQ CELYM",

B | \\TO ^ISLO POLOVITELXNO",

C | \\TO ^ISLO QWLQETSQ PROSTYM", D | \DANNOE ^ISLO DELITSQ NA TRI".

pEREWEDITE NA OBY^NYJ QZYK SLEDU@]IE FORMULY: A _ B, A & B, A _ :A, B & :B, D C, (A & C) ! :D, (A & D) ! :C, (A _ B) & (C _ D), :A _ :D, (A & B & C) _ D.

kAKIE IZ SFORMULIROWANNYH WYSKAZYWANIJ QWLQ@TSQ ISTINNYMI?

3.sOSTAWXTE TABLICU LOGI^ESKIH WOZMOVNOSTEJ DLQ FORMULY OT TREH BUKW. dLQ FORMULY OT ^ETYREH BUKW.

4.dOKAVITE, ^TO FORMULA OT n BUKW IMEET 2n LOGI^ESKIH WOZMOVNOSTEJ.

5.pRIDUMAJTE UDOBNYJ SPOSOB POSTROENIQ TABLICY LOGI^ESKIH WOZMOVNOSTEJ DLQ FORMULY OT n BUKW.

6.dOKAVITE TEOREMU P. III.1.5. I P. III.1.7.

7.wNIMATELXNO IZU^ITE DOKAZATELXSTWO ODNOGO IZ ZAKONOW POGLO]ENIQ, PRIWEDENNOE NIVE.

a & (a _ b) a

a) pUSTX W NEKOTOROJ LOGI^ESKOJ WOZMOVNOSTI FORMULA a & (a _ b) PRINIMAET ZNA^ENIE, RAWNOE 1, TO ESTX a & (a _ b) = 1. pO OPREDELENI@ OPERACII & OTS@DA SLEDUET, ^TO a = 1. tAK ^TO, ESLI a & (a _ b) = 1, TO I a = 1.

B) pUSTX TEPERX W KAKOJ-TO LOGI^ESKOJ WOZMOVNOSTI a & (a _ b) = 0. pO OPREDELENI@

OPERACII &, OTS@DA SLEDUET, ^TO a = 0 ILI VE a _ b = 0. eSLI a _ b = 0, TO IZ OPREDELENIQ OPERACII _ WYTEKAET, ^TO a = 0. tAKIM OBRAZOM, WSE RAWNO a = 0. tO ESTX,

ESLI a & (a _ b) = 0, TO I a = 0.

iZ A) I B) POLU^AEM, ^TO FORMULY a & (a _ b) I a W L@BOJ LOGI^ESKOJ WOZMOVNOSTI PRINI- MA@T ODINAKOWYE ZNA^ENIQ ISTINNOSTI, ^TO OZNA^AET, ^TO \TI FORMULY RAWNOSILXNY.

wOSPROIZWEDITE SHEMU PRIWEDENNOGO SPOSOBA DOKAZATELXSTWA RAWNOSILXNOSTI FORMUL. ~TO WY MOVETE SKAZATX O TAKOM METODE I METODE SOSTAWLENIQ TABLIC ISTINNOSTI W PLANE IH SRAWNENIQ?

61

gLAWA III. aLGEBRA WYSKAZYWANIJ

8.sPOSOBOM, UKAZANNOM W PREDYDU]EM UPRAVNENII DOKAVITE ASSOCIATIWNOSTX OPERACII _, DISTRIBUTIWNOSTX OPERACII & OTNOSITELXNO _, NE DOKAZANNYJ WAMI ZAKON DE-mORGANA, PRA- WILA ISKL@^ENIQ IMPLIKACII I \KWIWALENCII.

9.iSPOLXZUQ LI[X ZAKONY POGLO]ENIQ I DISTRIBUTIWNYE ZAKONY, DOKAZATX ZAKONY IDEMPO- TENTNOSTI.

10.sLEDU@]IE FORMULY PRIWESTI K BOLEE PROSTOMU WIDU:

(a)(a & :b) _ (a & :c) _ (b & c) _ b _ c,

(b)(a & b & c) _ (a & b & :c) _ (a & :b),

(c):((a ! b) & (b ! :a)),

(d)(a ! :b) _ :(a _ b),

(e):(:a & :b) _ ((a ! b) & a).

11.dOKAVITE, ^TO KAVDAQ FORMULA ALGEBRY WYSKAZYWANIJ RAWNOSILXNA FORMULE:

(a)NE SODERVA]EJ OPERACIJ IMPLIKACII I \KWIWALENCII I W KOTOROJ OPERACIQ OTRICANIQ OTNESENA LI[X K BUKWAM

(b)SODERVA]EJ LI[X OPERACII : I &

(c)SODERVA]EJ LI[X OPERACII : I _.

(d)SODERVA]EJ LI[X OPERACII : I !.

12.dOKAVITE TOVDESTWENNU@ ISTINNOSTX FORMUL, ISPOLXZUQ ZAKONY LOGIKI.

(a)a ! (b ! a),

(b)(a ! (b ! c)) ! ((a ! b) ! (a ! c)),

(c)(:b ! :a) ! ((:b ! a) ! b),

13.sKOLXKO POPARNO NERAWNOSILXNYH FORMUL MOVNO SOSTAWITX W ALFAWITE, SODERVA]EM W TO^- NOSTI n WYSKAZYWATELXNYH PEREMENNYH?

62

x 2. sOWER[ENNYE NORMALXNYE FORMY. pRIMENENIE ALGEBRY WYSKA- ZYWANIJ K PEREKL@^ATELXNYM SHEMAM

pOSTROENIE FORMUL PO ZADANNYM TABLICAM ISTINNOSTI. nORMALXNYE DIZ_@NKTIWNYE (KON_- @NKTIWNYE) FORMY. sOWER[ENNYE NORMALXNYE DIZ_@NKTIWNYE (KON_@NKTIWNYE) FORMY. lOGI^ESKIE OPERACII NAD DWUHPOL@SNYMI PEREKL@^ATELQMI. zADA^I SINTEZA I ANALIZA PE- REKL@^ATELXNYH SHEM.

2.1.pOSTROENIE FORMUL PO ZADANNYM TABLICAM ISTINNOSTI. rASSMOTRIM WNA^ALE

RE[ENIE \TOJ ZADA^I NA PRIMERE. pUSTX FORMULA a = a(A1 A2 A3) OT TREH WYSKAZYWATELXNYH PEREMENNYH ZADANA TAKOJ TABLICEJ ISTINNOSTI (SM. TABLICU 7).

tABL. 7: tABLICA ISTINNOSTI FORMULY OT TREH WYSKAZYWATELXNYH PEREMENNYH.

pONQTNO, ^TO SU]ESTWUET BESKONE^NO MNOGO RAWNOSILXNYH FORMUL ALGEBRY WYSKAZYWANIJ, IME@]IH \TU TABLICU ISTINNOSTI. uKAVEM SPOSOB NAHOVDENIQ DWUH TAKIH FORMUL.

pOME^AEM TE STROKI TABLICY, W KOTORYH a(A1 A2 A3) PRINIMAET ZNA^ENIE, RAWNOE 1. |TO STROKI 1, 3, 7. dLQ KAVDOJ STROKI (LOGI^ESKOJ WOZMOVNOSTI) SOSTAWIM FORMULU, ISTINNU@ TOLXKO W \TOJ LOGI^ESKOJ WOZMOVNOSTI I LOVNU@ WO WSEH OSTALXNYH LOGI^ESKIH WOZMOVNOSTQH:

1-Q STROKA | A1 & A2 & A3

3-Q STROKA | A1 & :A2 & A3

7-Q STROKA | :A1 & :A2 & A3.

eSLI WOZXMEM TEPERX DIZ_@NKCI@ WSEH \TIH FORMUL, TO \TO I BUDET ISKOMOJ FORMULOJ:

rASSMOTRIM DRUGOE RE[ENIE \TOJ ZADA^I. pOME^AEM TEPERX TE STROKI TABLICY, W KOTORYH a(A1 A2 A3) PRINIMAET ZNA^ENIE, RAWNOE 0. |TO STROKI 2, 4, 5, 6, 8. dLQ KAVDOJ LOGI^ESKOJ WOZMOVNOSTI SOSTAWIM FORMULU, LOVNU@ TOLXKO W \TOJ LOGI^ESKOJ WOZMOVNOSTI I ISTINNU@ WO WSEH OSTALXNYH LOGI^ESKIH WOZMOVNOSTQH:

2-Q STROKA | :A1 _ :A2 _ A3

4-Q STROKA | :A1 _ A2 _ A3

5-Q STROKA | A1 _ :A2 _ :A3

6-Q STROKA | A1 _ :A2 _ A3

8-Q STROKA | A1 _ A2 _ A3.

eSLI TEPERX WOZXMEM KON_@NKCI@ \TIH FORMUL, TO \TO TAKVE BUDET ISKOMOJ, TO ESTX IME@]EJ ZADANNU@ TABLICU ISTINNOSTI, FORMULOJ:

a = (:A1 _:A2 _A3) & (:A1 _A2 _A3) & (A1 _:A2 _:A3) & (A1 _:A2 _A3) & (A1 _A2 _A3): (2)

63

gLAWA III. aLGEBRA WYSKAZYWANIJ

fORMULY (1) I (2) RAWNOSILXNY, TAK KAK IME@T ODNU I TU VE TABLICU ISTINNOSTI. oTMETIM, ^TO W DANNOM SLU^AE UDOBNEE STROITX FORMULU (1).

lEGKO PONQTX, ^TO PROWEDENNYE RASSUVDENIQ GODQTSQ I DLQ OB]EJ SITUACII, TO ESTX NAHOV- DENIQ FORMULY PO ZADANNOJ PROIZWOLXNOJ TABLICE ISTINNOSTI.

2.2.nORMALXNYE FORMY. dLQ KAVDOJ FORMULY ALGEBRY WYSKAZYWANIJ MOVNO UKAZATX

RAWNOSILXNU@ EJ FORMULU, SODERVA]U@ IZ LOGI^ESKIH SWQZOK LI[X OTRICANIE, KON_@NKCI@ I DIZ_@NKCI@. dLQ \TOGO DOSTATO^NO WOSPOLXZOWATXSQ PRAWILAMI UDALENIQ IMPLIKACII I \KWIWA-

LENCII (SM. III.1.7.). rASSMOTRENIE OSOBOGO WIDA TAKIH FORMUL I SOSTAWLQET CELX POSLEDU@]IH TREH PUNKTOW.

oPREDELENIE 1. kON_@NKTIWNYM ODNO^LENOM OT WYSKAZYWATELXNYH PEREMENNYH A1 : : : An NAZYWAETSQ KON_@NKCIQ \TIH PEREMENNYH ILI IH OTRICANIJ.

nAPRIMER, FORMULY

A1 & :A2 & A3

A2 & A3 & :A2 & A5

A1 & A2 & :A1 & A3 & A1

QWLQ@TSQ KON_@NKTIWNYMI ODNO^LENAMI.

oPREDELENIE 2. dIZ_@NKTIWNYM ODNO^LENOM OT WYSKAZYWATELXNYH PEREMENNYH A1 : : : An NAZYWAETSQ DIZ_@NKCIQ \TIH PEREMENNYH ILI IH OTRICANIJ.

nAPRIMER, FORMULY

:A1 _ A2 _ A4

A3 _ A3 _ A3

:A1 _ A5 _ A4 _ :A4

QWLQ@TSQ DIZ_@NKTIWNYMI ODNO^LENAMI.

oPREDELENIE 3. dIZ_@NKTIWNOJ NORMALXNOJ FORMOJ NAZYWAETSQ DIZ_@NKCIQ KON_@NKTIW- NYH ODNO^LENOW, TO ESTX WYRAVENIE WIDA a1 _ a2 _ : : : _ ak, GDE WSE ai, i = 1 2 : : : k QWLQ@TSQ KON_@NKTIWNYMI ODNO^LENAMI (NE OBQZATELXNO RAZLI^NYMI).

oPREDELENIE 4. kON_@NKTIWNOJ NORMALXNOJ FORMOJ NAZYWAETSQ KON_@NKCIQ DIZ_@NKTIW- NYH ODNO^LENOW b1 & b2 & : : : & bl, GDE WSE bi, i = 1 2 : : : l QWLQ@TSQ DIZ_@NKTIWNYMI ODNO- ^LENAMI (NE OBQZATELXNO RAZLI^NYMI).

tAKVE BUDEM NAZYWATX DIZ_@NKTIWNOJ (KON_@NKTIWNOJ) NORMALXNOJ FORMOJ UKAZANNYE WY- RAVENIQ PRI k = 1 ILI l = 1.

nORMALXNU@ FORMU, PREDSTAWLQ@]U@ FORMULU a (TO ESTX RAWNOSILXNU@ a) BUDEM NAZYWATX

PROSTO NORMALXNOJ FORMOJ \TOJ FORMULY.

nETRUDNO PONQTX ^TO WSQKAQ FORMULA OBLADAET KAK DIZ_@NKTIWNOJ, TAK I KON_@NKTIWNOJ NORMALXNYMI FORMAMI. bOLEE TOGO, U DANNOJ FORMULY a SU]ESTWUET NEOGRANI^ENO MNOGO KAK DIZ_@NKTIWNYH, TAK I KON_@NKTIWNYH NORMALXNYH FORM.

2.3.sOWER[ENNYE NORMALXNYE FORMY. sREDI MNOVESTWA DIZ_@NKTIWNYH (RAWNO KAK

I KON_@NKTIWNYH) NORMALXNYH FORM, KOTORYMI OBLADAET DANNAQ FORMULA ALGEBRY WYSKAZYWA- NIJ, SU]ESTWUET UNIKALXNAQ FORMA: ONA EDINSTWENNA DLQ DANNOJ FORMULY. |TO TAK NAZYWAEMAQ SOWER[ENNAQ DIZ_@NKTIWNAQ NORMALXNAQ FORMA (SREDI KON_@NKTIWNYH FORM | SOWER[ENNAQ KON_@NKTIWNAQ NORMALXNAQ FORMA).

oPREDELENIE 1. oDNO^LEN (KON_@NKTIWNYJ ILI DIZ_@NKTIWNYJ) OT WYSKAZYWATELXNYH PE- REMENNYH A1 : : : An NAZYWAETSQ SOWER[ENNYM, ESLI W NEGO OT KAVDOJ PARY FORMUL Ai :Ai (i = 1 2 : : : n) WHODIT ROWNO ODNA FORMULA.

nORMALXNAQ FORMA (DIZ_@NKTIWNAQ ILI KON_@NKTIWNAQ) OT PEREMENNYH A1 : : : An NAZYWA- ETSQ SOWER[ENNOJ OT \TIH PEREMENNYH, ESLI W NEE WHODQT LI[X NEPOWTORQ@]IESQ SOWER[ENNYE ODNO^LENY (KON_@NKTIWNYE ILI DIZ_@NKTIWNYE SOOTWETSTWENNO) OT A1 : : : An

64

x 2. sOWER[ENNYE NORMALXNYE FORMY. pRIMENENIE ALGEBRY WYSKAZYWANIJ K PEREKL@^ATELXNYM SHEMAM

nAPRIMER, FORMULA

(A & B) _ (:A & B) _ (A & :B)

QWLQETSQ SOWER[ENNOJ DIZ_@NKTIWNOJ FORMOJ OT WYSKAZYWATELXNYH PEREMENNYH A I B. pRI- MERAMI SOWER[ENNOJ KON_@NKTIWNOJ I DIZ_@NKTIWNOJ FORM QWLQ@TSQ TAKVE FORMULY (2) I (1) SOOTWETSTWENNO.

2.4. pREDSTAWLENIE FORMUL ALGEBRY WYSKAZYWANIJ SOWER[ENNYMI NORMALXNY- MI FORMAMI.

tEOREMA 1. kAVDAQ NE TOVDESTWENNO LOVNAQ FORMULA ALGEBRY WYSKAZYWANIJ IMEET EDINST- WENNU@ (S TO^NOSTX@ DO PERESTANOWKI DIZ_@NKTIWNYH ^LENOW) SOWER[ENNU@ DIZ_@NKTIWNU@ NORMALXNU@ FORMU.

tEOREMA 2. kAVDAQ FORMULA ALGEBRY WYSKAZYWANIJ, KOTORAQ NE QWLQETSQ TAWTOLOGIEJ, IME- ET EDINSTWENNU@ (S TO^NOSTX@ DO PERESTANOWKI KON_@NKTIWNYH ^LENOW) SOWER[ENNU@ KON_- @NKTIWNU@ NORMALXNU@ FORMU.

2.5.lOGI^ESKIE OPERACII NAD DWUHPOL@SNYMI PEREKL@^ATELQMI. rASSMOTRIM

DWUHPOL@SNYE PEREKL@^ATELI, TO ESTX TAKIE, KOTORYE IME@T DWA SOSTOQNIQ: \ZAMKNUTO" | 1 I \RAZOMKNUTO" | 0. bUDEM IH OBOZNA^ATX BOLX[IMI LATINSKIMI BUKWAMI I NA SHEMAH IZOBRAVATX TAK:

A

rIS. III.1.

pEREKL@^ATELX, KOTORYJ SBLOKIROWAN S PEREKL@^ATELEM A TAK, ^TO ON ZAMKNUT, ESLI A RA- ZOMKNUT, I RAZOMKNUT, ESLI A ZAMKNUT, NAZOWEM INWERSNYM I BUDEM OBOZNA^ATX :A (SRAWNITE S OPERACIEJ OTRICANIQ NAD WYSKAZYWANIQMI). oPERACI@ POSLEDOWATELXNOGO SOEDINENIQ DWUH PE- REKL@^ATELEJ BUDEM OBOZNA^ATX &:

A & B

rIS. III.2.

sRAWNITE S OPERACIEJ KON_@NKCII WYSKAZYWANIJ.

oPERACI@ PARALLELXNOGO SOEDINENIQ DWUH PEREKL@^ATELEJ OBOZNA^IM ^EREZ _:

A

_

B

rIS. III.3.

sRAWNITE S OPERACIEJ DIZ_@NKCII WYSKAZYWANIJ.

tAKIM OBRAZOM, WSQKU@ FORMULU ALGEBRY WYSKAZYWANIJ OT SWQZOK :, &, _ MOVNO TRAKTO- WATX KAK NEKOTORU@ POSLEDOWATELXNO-PARALLELXNU@ SHEMU OT DWUHPOL@SNYH PEREKL@^ATELEJ. sOWER[ENNO O^EWIDNO, ^TO WSE SWOJSTWA OPERACIJ :, &, _ NAD WYSKAZYWANIQMI PERENOSQTSQ NA SOOTWETSTWU@]IE OPERACII NAD PEREKL@^ATELQMI (POSLEDOWATELXNO-PARALLELXNYMI SHEMAMI). tAKIM OBRAZOM, MY IMEEM ALGEBRU PEREKL@^ATELXNYH SHEM.

65

gLAWA III. aLGEBRA WYSKAZYWANIJ

2.6.zADA^I SINTEZA I ANALIZA PEREKL@^ATELXNYH SHEM. oTME^ENNU@ WY[E SWQZX

MEVDU ALGEBROJ WYSKAZYWANIJ I ALGEBROJ PEREKL@^ATELXNYH SHEM KOROTKO MOVNO WYRAZITX TAK: \TI ALGEBRY ODINAKOWO USTROENY (IZOMORFNY). |TOT IZOMORFIZM MOVET BYTX ISPOLXZOWAN PRI RE[ENII ZADA^ SLEDU@]IH DWUH TIPOW, KOTORYE USLOWNO NAZOWEM ANALIZ SHEM I SINTEZ SHEM.

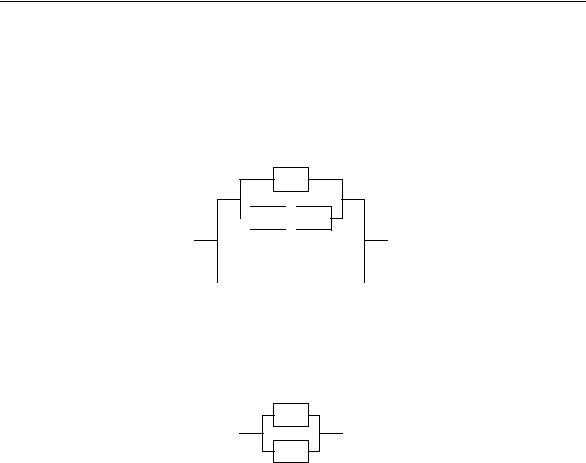
1. aNALIZ SHEM ZAKL@^AETSQ W SLEDU@]EM. dLQ DANNOJ SHEMY SOSTAWLQETSQ SOOTWETSTWU@- ]AQ FORMULA, KOTORAQ NA OSNOWANII ZAKONOW LOGIKI UPRO]AETSQ I DLQ NEE STROITSQ NOWAQ BOLEE PROSTAQ SHEMA, KOTORAQ (W SILU OTME^ENNOGO WY[E IZOMORFIZMA ALGEBR) OBLADAET TEMI VE \LEK- TRI^ESKIMI SWOJSTWAMI, ^TO I ISHODNAQ SHEMA. pRIWEDEM SOOTWETSTWU@]IJ PRIMER. dANA SHEMA

A

: A B

rIS. III.4.

zAPI[EM SOOTWETSTWU@]U@ EJ FORMULU I PREOBRAZUEM EE RAWNOSILXNYMI PREOBRAZOWANIQMI. (A _ (:A & B)) _ (A & B) A _ (:A & B) _ (A & B) A _ (A & B) _ (:A & B)

A _ (:A & B) (A _ :A) & (A _ B) 1 & (A _ B) A _ B. tAKIM OBRAZOM, ISHODNAQ SHEMA RAWNOSILXNA TAKOJ:

A

B

rIS. III.5.

2. sINTEZ SHEM ZAKL@^AETSQ W POSTROENII SHEM S ZADANNYMI \LEKTRI^ESKIMI SWOJSTWAMI. |TO DELAETSQ TAK. nA OSNOWANII ZADANNYH \LEKTRI^ESKIH SWOJSTW STROITSQ FORMULA ALGEBRY WYSKAZYWANIJ, A PO NEJ SOOTWETSTWU@]AQ SHEMA. pRIWEDEM

pRIMER 1. aKTIW STUDEN^ESKOJ GRUPPY, SOSTOQ]IJ IZ TREH ^ELOWEK, HO^ET PRIMENITX \LEKTRI- ^ESKU@ SHEMU DLQ REGISTRACII TAJNOGO GOLOSOWANIQ PROSTYM BOLX[INSTWOM GOLOSOW. pOSTROIM TAKU@ SHEMU, ^TOBY KAVDYJ GOLOSU@]IJ \ZA" NAVIMAL SWO@ KNOPKU, A KAVDYJ GOLOSU@]IJ \PROTIW" NE NAVIMAL SOOTWETSTWU@]EJ KNOPKI. w SLU^AE PRINQTIQ RE[ENIQ DOLVNA ZAGORETXSQ SIGNALXNAQ LAMPO^KA.

rE[ENIE. pUSTX A, B, C | OBOZNA^A@T SOOTWETSTWENNO WYSKAZYWANIQ \1 { YJ ZA", \2 { OJ ZA", \3 { IJ ZA". sOSTAWIM TABLICU ISTINNOSTI FORMULY a(A B C), KOTOROJ BUDET SOOTWETSTWOWATX ISKOMAQ SHEMA.

tEPERX SPOSOBOM, UKAZANNYM W P. III.2.1., SOSTAWLQEM FORMULU a = a(A B C). a = (A & B & C) _ (A & B & :C) _ (A & :B & C) _ (:A & B & C):

66

x 2. sOWER[ENNYE NORMALXNYE FORMY. pRIMENENIE ALGEBRY WYSKAZYWANIJ K PEREKL@^ATELXNYM SHEMAM

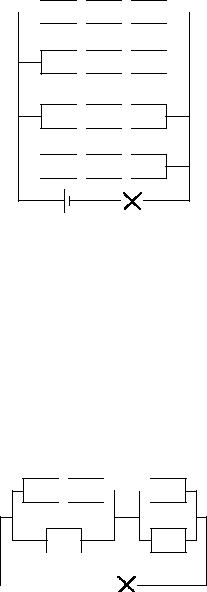
i, NAKONEC, SOSTAWIM SHEMU, KOTORAQ SOOTWETSTWUET POSTROENNOJ FORMULE (SM. RIS. III.6.). A B C

A B : C

A : B C

: A B C

rIS. III.6.

pOLU^ENNU@ W \TOM PRIMERE SHEMU MOVNO UPROSTITX, OSU]ESTWLQQ EE ANALIZ. rAWNOSILXNYMI PREOBRAZOWANIQMI UPRO]AEM FORMULU:

a = (A & B & C) _ (A & B & :C) _ (A & :B & C) _ (:A & B & C)(A & B & (C _ :C)) _ ((A _ :A) & (A _ B) & (A _ C) &

& (:B _ :A) & (:B _ B) & (:B _ C) & (C _ :A) & (C _ B) & (C _ C))

(A & B) _ (C & (A _ C) & (C _ B) & (C _ :A) & (C _ :B) & (A _ B) & (:B _ :A))(A & B) _ (C & (A _ B) & (:A _ :B)) (A & B) _ (C & (A _ B) & :(A & B))

((A & B) _ C) & ((A & B) _ A _ B) & ((A & B) _ :(A & B)) ((A & B) _ C) & (A _ B) uPRO]ENNAQ SHEMA PRIWEDENA NA RIS. III.7.

A B A

C B

rIS. III.7.

2.7.nOWYE TERMINY. kON_@NKTIWNYJ (DIZ_@NKTIWNYJ) ODNO^LEN. nORMALXNAQ KON_-

@NKTIWNAQ (DIZ_@NKTIWNAQ) FORMA. sOWER[ENNYJ KON_@NKTIWNYJ (DIZ_@NKTIWNYJ) ODNO^LEN. sOWER[ENNAQ NORMALXNAQ KON_@NKTIWNAQ (DIZ_@NKTIWNAQ) FORMA. dWUHPOL@SNOJ PEREKL@^A- TELX. iNWERSNYJ K DANNOMU PEREKL@^ATELX. oPERACII POSLEDOWATELXNOGO I PARALLELXNOGO SO- EDINENIQ PEREKL@^ATELEJ. aLGEBRA PEREKL@^ATELXNYH SHEM. aNALIZ I SINTEZ SHEM.

2.8.kONTROLXNYE WOPROSY.

1.iZWESTNO, ^TO FORMULA a = a(A B C) ISTINA W ODNOM EDINSTWENNOM SLU^AE: a(1 1 0) = 1. zAPI[ITE \TU FORMULU.

2. iZWESTNO, ^TO FORMULA a = a(A B C) ISTINA W TO^NOSTI W DWUH SLU^AQH: a(0 1 0) =

= a(0 0 0) = 1. zAPI[ITE \TU FORMULU.

3.kAKIM SHEMAM SOOTWETSTWU@T RAWNOSILXNYE FORMULY?

67

gLAWA III. aLGEBRA WYSKAZYWANIJ

4.kAKOJ SHEME SOOTWETSTWUET TOVDESTWENNO ISTINNAQ FORMULA? tOVDESTWENNO LOVNAQ?

5.pERESKAVITE SMYSL ANALIZA SHEM.

6.pERESKAVITE SMYSL SINTEZA SHEM.

2.9.uPRAVNENIQ.

1.pOSTROJTE FORMULU OT TREH BUKW, ISTINNU@ TOGDA I TOLXKO TOGDA, KOGDA W TO^NOSTI DWE BUKWY PRINIMA@T ZNA^ENIE, RAWNOE 1. kOGDA W TO^NOSTI ODNA BUKWA PRINIMAET ZNA^ENIE, RAWNOE 0.

2.pRIDUMAJTE FORMULU OT TREH BUKW, LOVNU@ W ODNOM EDINSTWENNOM SLU^AE, KOGDA A = 1,

B = 0, C = 1. kOGDA A = 0, B = 1, C = 1.

A

: A : B

B

rIS. III.8.

6.iMEETSQ ODNA LAMPO^KA W LESTNI^NOM PROLETE DWUH\TAVNOGO ZDANIQ. pOSTROJTE SHEMU TAK, ^TOBY NA KAVDOM \TAVE SWOIM WYKL@^ATELEM MOVNO BYLO BY GASITX I ZAVIGATX LAMPU NEZAWISIMO OT POLOVENIQ DRUGOGO PEREKL@^ATELQ.

7.nEOBHODIMO, ^TOBY W BOLX[OM ZALE MOVNO BYLO WKL@^ATX I WYKL@^ATX SWET PRI POMO]I L@BOGO IZ TREH PEREKL@^ATELEJ, RASPOLOVENNYH NA TREH STENAH. sOSTAWXTE TAKU@ SHEMU.

8.gRUPPA STUDENTOW SDAET ZA^ET, SOSTOQ]IJ IZ 4-H WOPROSOW, TREBU@]IH USTANOWITX ISTIN- NOSTX ILI LOVNOSTX KAKIH-TO UTWERVDENIJ. pOSTROITX SHEMU, POZWOLQ@]U@ OTWE^ATX NA KAVDYJ WOPROS NAVATIEM ILI NENAVATIEM SOOTWETSTWU@]EJ KNOPKI. sHEMA DOLVNA PRI \TOM POKAZYWATX KOLI^ESTWO PRAWILXNYH OTWETOW.

9.sOSTAWXTE SHEMU S ^ETYRXMQ PEREKL@^ATELQMI, KOTORAQ PROWODIT TOK TOGDA I TOLXKO TOGDA, KOGDA ZAMYKA@TSQ NE WSE PEREKL@^ATELI, A TOLXKO NEKOTORYE IZ NIH.

10.nA^ERTITE SHEMU S 5 PEREKL@^ATELQMI, KOTORAQ ZAMYKAETSQ, ESLI I TOLXKO ESLI ZAMKNUTY ROWNO 4 IZ \TIH PEREKL@^ATELEJ.

68

x 3. pOLNYE SISTEMY SWQZOK

oPREDELENIE POLNOJ SISTEMY SWQZOK. sWOJSTWA POLNYH SISTEM SWQZOK. oPISANIE P. S. S. IZ . oDNO\LEMENTNYE P. S. S. iSKL@^ITELXNOSTX SWQZOK & I _.

3.1.oPREDELENIE POLNOJ SISTEMY SWQZOK. rANEE BYLI ODNOZNA^NO OPREDELENY PQTX

OSNOWNYH LOGI^ESKIH SWQZOK, ISPOLXZUEMYH W QZYKE ALGEBRY WYSKAZYWANIJ DLQ ZAPISI FORMUL. oBOZNA^IM:

= f: & _ ! g:

oTMETIM, ^TO ^TO MOVNO WWESTI I DRUGIE SWQZKI (OPREDELITX TABLICAMI ISTINNOSTI), OT- LI^NYE OT SWQZOK IZ .

wSEGO RAZLI^NYH UNARNYH SWQZOK MOVNO OPREDELITX 4, A BINARNYH | 16 (SM. UPR. 1). w VE WSEGO ODNA UNARNAQ SWQZKA I 4 BINARNYH. sWQZKI IZ BUDEM NAZYWATX OSNOWNYMI SWQZKAMI. mNO- VESTWO WSEH UNARNYH I BINARNYH SWQZOK (A WSEGO IH 20) OBOZNA^IM ^EREZ . pONQTNO, ^TO . eSLI 1 | NEKOTOROE MNOVESTWO SWQZOK, TO ESTX 1 , TO OBOZNA^IM ^EREZ f 1g MNOVESTWO WSEWOZMOVNYH FORMUL aw, W ZAPISI KOTORYH MOGUT U^ASTWOWATX LI[X SWQZKI IZ 1. iNA^E GO- WORQ, f 1g SOSTOIT IZ FORMUL, NE SODERVA]IH W SWOEJ ZAPISI SWQZOK IZ n 1. tAK, NAPRIMER, PROSTEJ[IE FORMULY, TO ESTX BUKWY LATINSKOGO ALFAWITA, SNABVENNYE, BYTX MOVET, [TRIHA- MI ILI INDEKSAMI, WHODQT W f 1g DLQ L@BOGO PODMNOVESTWA 1 MNOVESTWA . iZ OPREDELENIQf 1g NEPOSREDSTWENNO SLEDU@T O^EWIDNYE SWOJSTWA 1{2.

1. f g | MNOVESTWO WSEWOZMOVNYH FORMUL ALGEBRY WYSKAZYWANIJ (aw). 2. eSLI 1 2 , TO f 1g f 2g.

oPREDELENIE 1. mNOVESTWO 1 SWQZOK IZ NAZYWAETSQ POLNOJ SISTEMOJ SWQZOK (P. S. S.), ESLI WSQKAQ FORMULA IZ f g RAWNOSILXNA NEKOTOROJ FORMULE IZ f 1g.

pRIMER 1. eSLI W KA^ESTWE 1 WOZXMEM , TO PONQTNO, ^TO WSQKAQ FORMULA IZ ( ) RAWNOSILXNA NEKOTOROJ FORMULE IZ f g. tAKIM OBRAZOM, | POLNAQ SISTEMA SWQZOK.

pRIMER 2. pOLXZUQSX PRAWILOM ISKL@^ENIQ \KWIWALENCII

a b (a ! b) & (b ! a)

RAWNOSILXNYMI PREOBRAZOWANIQMI WSQKU@ FORMULU MOVNO PRIWESTI K WIDU, W KOTOROM NET OPERA- CII . sLEDOWATELXNO, WSQKAQ FORMULA IZ f g RAWNOSILXNA NEKOTOROJ FORMULE IZ f: & _ !g. |TO OZNA^AET, ^TO MNOVESTWO f: & _ !g | P. S. S.

3.2.sWOJSTWA POLNYH SISTEM SWQZOK.

tEOREMA 1. pOLNYE SISTEMY SWQZOK OBLADA@T SLEDU@]IMI SWOJSTWAMI:

1)ESLI KAKOE-TO MNOVESTWO SWQZOK 1 SODERVIT NEKOTORU@ P. S. S., TO 1 | TOVE P. S. S.

2)ESLI 1 | P. S. S. I WSQKAQ FORMULA IZ ( 1) RAWNOSILXNA KAKOJ-TO FORMULE IZ ( 2) DLQ NEKOTOROJ SISTEMY SWQZOK 2, TO 2 TOVE P. S. S.

dOKAZATELXSTWO. 1) nEPOSREDSTWENNO SLEDUET IZ OPREDELENIQ P. S. S.

2) pUSTX a 2 ( ). tAK KAK 1 | P. S. S., TO a b DLQ NEKOTOROJ FORMULY b IZ ( 1). pO USLOWI@ b c DLQ NEKOTOROJ c IZ ( 2). pO TRANZITIWNOSTI OTNO[ENIQ RAWNOSILXNOSTI IMEEM:

a c I c 2 ( 2)

|TO OZNA^AET, ^TO 2 | P. S. S.

pRIMER 1. pOLXZUQSX PRAWILOM ISKL@^ENIQ IMPLIKACII

a ! b :a _ b

RAWNOSILXNYMI PREOBRAZOWANIQMI WSQKU@ FORMULU aw IZ f: & _ !g MOVNO PRIWESTI K WIDU, W KOTOROM NET OPERACII !. |TO OZNA^AET, ^TO WSQKAQ FORMULA IZ f: & _ !g RAWNOSILXNA

NEKOTOROJ FORMULE IZ f: & _g I f: & _ !g | P. S. S., SM. PRIMER 3.1.2. pRIMENQQ P. 2 TEOREMY 3.2.1, POLU^AEM, ^TO f: & _g | P. S. S.

69

gLAWA III. aLGEBRA WYSKAZYWANIJ

tEOREMA 2. wSQKAQ POLNAQ SISTEMA SWQZOK IZ SODERVIT SWQZKU :.

dOKAZATELXSTWO. pUSTX M | MNOVESTWO WSEH FORMUL aw, NE SODERVA]IH W SWOEJ ZAPISI

SWQZKI :, TO ESTX M = f& _ ! g. lEGKO UBEDITXSQ W TOM, ^TO ESLI a(A1 : : : An) 2 M, TO a(1 : : : 1) = 1. rASSMOTRIM FORMULU b(A B) = :A & B. o^EWIDNO, b(1 1) = 0, ZNA^IT b(A B) 2 f g, NO b(A B) NERAWNOSILXNA NIKAKOJ FORMULE IZ f& _ ! g. |TO OZNA^AET,

^TO MNOVESTWO f& _ ! g NE QWLQETSQ P. S. S. pO TEOREME 3.2.1, P. 1, NIKAKOE PODMNOVESTWO MNOVESTWA f& _ ! g NE QWLQETSQ P. S. S. |TO I OZNA^AET, ^TO WSQKAQ P. S. S. IZ OBQZANA

SODERVATX OPERACI@ :.

3.3.oPISANIE POLNYH SISTEM SWQZOK IZ . pO TEOREME 3.2.2, WSQKAQ P. S. S. IZ

SODERVIT :. wOZNIKAET WOPROS O TOM, A NE QWLQETSQ LI ODNO\LEMENTNOE MNOVESTWO f:g P. S. S.? oTWET DAET

tEOREMA 1. mNOVESTWO f:g NE QWLQETSQ P. S. S.

dOKAZATELXSTWO. oTMETIM, ^TO f:g SOSTOIT IZ WSEH BUKW ALFAWITA I FORMUL WIDA :: : : :: A,

| {zn }

n 2 N. oDNAKO, NI ODNA IZ \TIH FORMUL NE QWLQETSQ TAWTOLOGIEJ. sLEDOWATELXNO, FORMULA A_:A, NAPRIMER, NERAWNOSILXNA NIKAKOJ FORMULE IZ f:g. sLEDOWATELXNO, MNOVESTWO f:g NE QWLQETSQ P. S. S.

tEOREMA 2. sLEDU@]IE NIVE MNOVESTWA SWQZOK IZ QWLQETSQ P. S. S.:

1)f: &g

2)f: _g

3)f: !g.

dOKAZATELXSTWO. 1) f: &g. w PRIMERE 3.2.1 POKAZANO, ^TO MNOVESTWO f: & _g | P. S. S. pOLX- ZUQSX RAWNOSILXNOSTX@

a _ b :(:a & :b)

WSQKU@ FORMULU IZ f: & _g RAWNOSILXNYMI PREOBRAZOWANIQMI MOVNO PRIWESTI K FORMULE, W ZAPISI KOTOROJ NET OPERACII _. |TO OZNA^AET, ^TO WSQKAQ FORMULA IZ f: & _g RAWNOSILXNA

NEKOTOROJ FORMULE IZ f: &g. a TAK KAK f: & _g | P. S. S., TO PO TEOREME 3.2.1, P. 2, f: &g | TOVE P. S. S.

2) f: _g. rASSUVDENIQ TAKIE VE, KAK I W PREDYDU]EM PUNKTE S ISPOLXZOWANIEM RAWNOSILX- NOSTI a & b :(:a _ :b).

3) f: !g. pOLXZUQSX RAWNOSILXNOSTX@ a _ b :a ! b, WSQKU@ FORMULU IZ f: _g RAWNO- SILXNYMI PREOBRAZOWANIQMI MOVNO PRIWESTI K FORMULE IZ f: !g, TO ESTX WSQKAQ FORMULA

IZ f: _g RAWNOSILXNA NEKOTOROJ FORMULE IZ f: !g I f: _g | P. S. S. sLEDOWATELXNO, PO TEOREME 3.2.1, P.2, f: !g | TOVE P. S. S.

sLEDSTWIE 1. wSQKAQ SISTEMA SWQZOK IZ , SODERVA]AQ SWQZKU : I HOTQ BY ODNU IZ SWQZOK &, _, !, QWLQETSQ P. S. S.

dOKAZATELXSTWO SLEDUET NEPOSREDSTWENNO IZ PREDYDU]EJ TEOREMY I TEOREMY 3.2.1, P. 1.

3.4.oDNO\LEMENTNYE POLNYE SISTEMY SWQZOK. w P. III.3.3. DOKAZANO, ^TO SREDI SWQZOK

IZ NET TAKOJ SWQZKI, KOTORAQ SOSTAWLQLA BY P. S. S. eSTX LI TAKIE SWQZKI NE W ? oTWET POLOVITELXNYJ. wWEDEM DWE SWQZKI, KOTORYE OBOZNA^IM & I _, A SMYSL IH OPREDELIM TABLICAMI ISTINNOSTI:

70