
- •Теория множеств.
- •Свойства подмножеств.
- •Операции над множествами.
- •Алгебра теории множеств.
- •Решение уравнений алгебры множеств.
- •Кортеж.
- •Проекция множества.
- •График и свойства графика
- •Свойства графиков.
- •Прямое (декартовое) произведение множество.
- •Соответствия.
- •Отношения.
- •Операции над отношениями.
- •Основные свойства отношений.
- •Решетки. Диаграммы Хассе.
- •Математическая логика Высказывания и операции над высказываниями.
- •Операции над высказываниями.
- •Формулы математической логики.
- •Формулы равносильности.
- •Различные формы представления высказываний
- •Выполнимость формулы алгебры логики
- •Применение математической логики.
- •Минимизация сложных высказываний.
- •Метод Квайна.
- •Метод минимизирующих карт.
- •Метод минимизации с помощью карт Вейча.
- •Булевые функции и их свойства.
- •Функциональная полнота. Теорема Поста.
- •Логика предикат.
- •Логические операции над предикатами.
- •Квантовые операции.
- •Равносильные формулы логики предикатов.
- •Предваренная нормальная форма предиката
- •Теория графов
- •Основные понятия теории графов
- •Эйлеров граф.
- •Множество внутренней устойчивости графа
- •Алгоритм Магу для определения множества внутренней устойчивости графа
- •Множество внешней устойчивости графа
- •Алгоритм Магу для определения множества внешней устойчивости.
- •Множество путей в графе
- •Алгоритм фронта волны. Поиск минимального пути в графе.
- •Алгоритм фронта волны.
- •Ярусно-параллельная форма графов
- •Деревья и леса
- •Алгоритм получения дерева из графа
- •Теория алгоритмов
- •Рекурсивная функция
- •Пусть даны функции:
- •Машина Тьюринга
- •Работа машины Тьюринга:
- •Нормальные алгоритмы Маркова
- •Теория автоматов
- •Законы функционирования автоматов.
- •Задание автоматов
- •Минимизация автоматов
- •Алгоритм минимизации автомата Мили
- •Особенности минимизации автомата Мура. :
- •Минимизация частичных автоматов.
- •Переход от автомата Мили к автомату Мура
- •Переход от автомата Мура к автомату Мили
Отношения.
Отношением
называется
пара вида
![]() такая, чтоФ2
(M2=M
такая, чтоФ2
(M2=M![]() M),где
Ф
- график отношения, М
- это множество, между элементами которого
существует данное отношение.
M),где
Ф
- график отношения, М
- это множество, между элементами которого
существует данное отношение.
ПРИМЕР.
Пусть
дано
![]() ,
где
,
где![]() ,
а график отношения определяется как
,
а график отношения определяется как![]() .
Это отношение ”X больше Y” на множестве
натуральных чисел. Данное отношение
задано описанием свойств. Перечислением
данное отношение может быть задано
следующим образом:
.
Это отношение ”X больше Y” на множестве
натуральных чисел. Данное отношение
задано описанием свойств. Перечислением
данное отношение может быть задано
следующим образом:
,
где >
Отношение называется полным, если 2.
Отношение называется отношением равенства, если {<x,xy,y.
Отношение называется отношением неравенства, если 2\.
Запись xy означает, что между x и y существует отношение .
Операции над отношениями.
Пусть даны два отношения и r=R,M>. Над данными отношениями могут быть выполнены следующие операции:
объединение
 r=<
r=<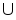 R,M>.
R,M>.пересечение
 r=<Ф
r=<Ф R,M>.
R,M>.дополнение
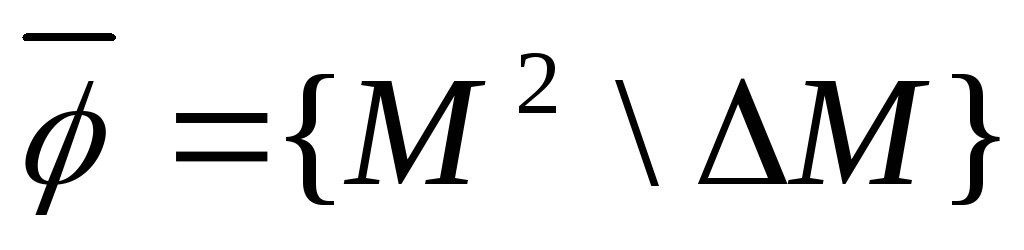
разность \r=<Ф\R,M>.
композиция
 r=<Ф
r=<Ф R,M>.
R,M>.инверсия -1=<Ф-1,M>.
Основные свойства отношений.
Рефлексивность.
Отношение называется рефлексивным, если для всех x выполняется условие: xx или .
Антирефлексивность.
Отношение
называется антирефлексивным,
если для всех x
выполняется
условие: xx
(символ ““
означает “не выполняется”) или
![]() .
.
Симметричность.
Отношение называется симметричным , если для всех x выполняется условие: xy yx или Ф=Ф-1.
Антисимметричность.
Отношение
называется антисимметричным,
если для всех x
выполняется условие: xy
и xy
yx
или
![]() .
.
Асимметричность.
Отношение
называется асимметричным,
если для всех x
выполняется условие:
xy
yx
или
![]() =.
=.
Связность (полнота).
Отношение
называется связным
(полным),
если для всех x
выполняется условие: xy
xy
или yx
или М2\![]() .
.
Транзитивность.
Отношение
называется транзитивным,
если для всех x
выполняется условие:
xy
и yz
xz
или Ф![]() ФФ.
ФФ.
ПРИМЕР
Какими свойствами обладает отношение =<Ф,X>, где X={1; 2; а},
Ф={<1,1>;<a,a>;<a,2>;<2,2>}.
Определим Ф-1, X:
Ф-1={<1,1>;<a,a>;<2,a>;<2,2>}
X={<1,1>;<2,2>;<a,a>}.
Отношение является:
- рефлексивным, так как XФ;
-
антисимметричным, так как
![]() X;
X;
-
транзитивным, так как
Ф![]() Ф={<1,1>;<a,a>;<a,2>;<2,2>}Ф;
Ф={<1,1>;<a,a>;<a,2>;<2,2>}Ф;
-
несвязное,
так
как
X2\X={<1,2>;<1,a>;<2,1>;<2,a>;<a,1>;<a,2>}
Ф![]() Ф-1={<1,1>;<a,a>;<a,2>;<2,2>;<2,a>}.
Ф-1={<1,1>;<a,a>;<a,2>;<2,2>;<2,a>}.
Отношение называется отношением эквивалентности, если оно рефлексивное, симметричное и транзитивное.
Отношение
называется отношением
нестрогого (частичного) порядка
(![]() ), если
оно рефлексивное, антисимметричное и
транзитивное.
), если
оно рефлексивное, антисимметричное и
транзитивное.
Отношение
называется совершенно
нестрого порядка
(![]() ),
если оно
рефлексивное, антисимметричное,
транзитивное и связное.
),
если оно
рефлексивное, антисимметричное,
транзитивное и связное.
Отношение
называется строго
порядка
(![]() ),
если оно
антирефлексивное, антисимметричное и
транзитивное .
),
если оно
антирефлексивное, антисимметричное и
транзитивное .
Отношение
называется совершенно
строго порядка
(![]() ),
если оно
антирефлексивное, транзитивное и
связное.
),
если оно
антирефлексивное, транзитивное и
связное.
Решетки. Диаграммы Хассе.
Рассмотрим отношение частичного порядка: “быть подмножеством“ на множестве-степени М={1,2}.
, где
Ф={<{},{}>;<{},{1}>;<{},{2}>;<{},{1,2}>;<{1},{1}>;<{1},{1,2}>;<{2},{2}>;<{2},{1,2}>};<{1,2},{1,2}>}.
Графически данное отношение можно изобразить следующим образом:
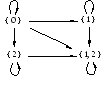
РИС 10 Графическое изображения отношения
Отношение является рефлексивным (графически это отображается петлями), антисимметричным ( графически - однонаправленные стрелки), транзитивным ( графически - транзитивными замыканиями вида:
Для отношений частичного порядка применимы диаграммы Хассе, которые строятся на основе обыкновенной диаграммы следующим образом:
рефлексивные петли и транзитивные связи не изображаются;
большие элементы ( элементы, в которые входят стрелки) располагают выше.
Таким образом, диаграмма Хассе для вышеприведенного примера будет выглядеть следующим образом:
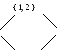
{
Ø } {
2 } {
1 }
РИС 11 Диаграмма Хассе
Для частично упорядоченного множества справедливо следующее:
Элемент аА называется наибольшим (наименьшим) , если для всех х А выполняется x
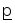 a ( a
a ( a x). Если наибольший (наименьший) элемент
существует, то он единственный.
x). Если наибольший (наименьший) элемент
существует, то он единственный.Элемент аА называется максимальным (минимальным) , если нет а множестве А элементов, больших (меньших), чем а. Максимальных (минимальных) элементов может быть несколько.
Пусть ВА. Элемент аА называется можарантой (минорантой) , если для всех х В этот элемент является наибольшим (наименьшим).
Множество мажорант В образует верхнюю границу множества В. Множество минорант В образует нижнюю границу множества В.
Наименьший элемент верхней границы называется точной верхней границей , или supremum ( sup ) B. Наибольший элемент нижней границы называется точной нижней границей, или infimum (inf) B.
Частично упорядоченное множество, у которого для любой пары элементов определен и существует sup и inf , называется решеткой.
ПРИМЕР
Пусть дано отношение, представленное на диаграмме Хассе

РИС 12 Диаграмма Хассе
Отношение А не является решеткой, т.к. элементы 7 и 8 не имеют sup.
Отношение В является решеткой, т.к. любая пара имеет sup и inf.
Алгебраическое представление решеток.
Введем
обозначения: sup(a,b)=a![]() b,
inf(a,b)=a
b,
inf(a,b)=a![]() b.
Для решетки справедливы следующие
свойства:
b.
Для решетки справедливы следующие
свойства:
1. Коммутативный:
a![]() b=b
b=b![]() a a
a a![]() b=b
b=b![]() a
a
2. Ассоциативный:
а![]() (в
(в![]() с)=(а
с)=(а![]() в)
в)![]() с а
с а![]() (в
(в![]() с)=(а
с)=(а![]() в)
в)![]() с
с
3. Идемпотентности:
а![]() а=а а
а=а а![]() а=а
а=а
4. Поглощения:
а![]() (а
(а![]() в)=а а
в)=а а![]() (а
(а![]() в)=а
в)=а
Решетки , для которой выполняется дистрибутивный закон:
а![]() (в
(в![]() с)=(а
с)=(а![]() в)
в)![]() (а
(а![]() с) а
с) а![]() (в
(в![]() с)=(а
с)=(а![]() в)
в)![]() (а
(а![]() с)
с)
называется дистрибутивной решеткой.
Решетка называется ограниченной, если он имеет максимальный и минимальный элемент.
ПРИМЕР
П
5

РИС 13 Диаграмма Хассе решетки
Решетка не является дистрибутивной, т.к. для элементов {2;3;4} не выполняется дистрибутивный закон:
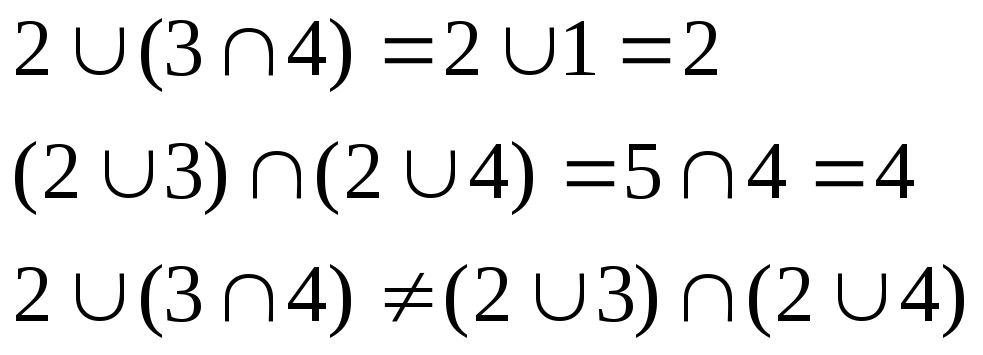
Дана решетка ,
где М={xx1, Ф={<x,y>xy. Эта решетка не является , так как не определен максимальный элемент (0.9999999999 ....) и минимальный элемент (0.0000000...1).
Обозначим
в ограниченной решетке максимальный
элемент 1, а минимальный элемент 0. Элемент
![]() называетсядополнением
элемента
а в данной решетке, если
называетсядополнением
элемента
а в данной решетке, если
![]() и
и![]() .
Решетка называется с дополнением, если
каждый элемент имеет хотя бы одно
дополнение.
.
Решетка называется с дополнением, если
каждый элемент имеет хотя бы одно
дополнение.
ПРИМЕР
Рассмотрим решетку, представленную на рис. 13. Найдем дополнения для каждого элемента решетки
![]()
Данная решетка является решеткой с дополнением.
Ограниченная дистрибутивная решетка с дополнением называется булевой решеткой.
На рис . 14 представлены дистрибутивные решетки

РИС. 14. Примеры булевых решеток
