Логика предикат.

Предикат  это сложное высказывание, в котором аргументы принимают значение из некоторой вещественной области, а значение самого высказывания принимает значение истинно или ложно.

ПРИМЕР

Предикатом является высказывание – быть четным числом на множестве натуральных чисел:

- быть четным числом;

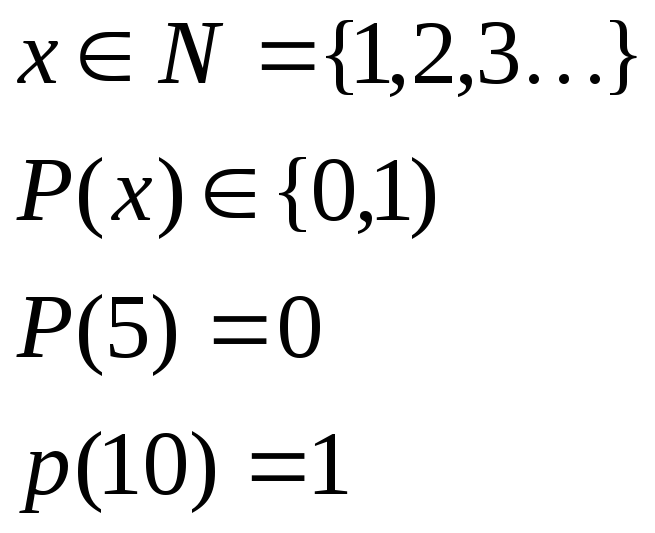
Предикаты могут быть одноместные - , двухместные -и многоместные -

Логические операции над предикатами.

Для предикатов выполнимы следующие операции:

Конъюнкция -это новый предикат, который принимает значение истинно при тех и только тех значениях из вещественной области, при которых оба предиката и истинны одновременно, и ложно во всех других случаях.

Дизъюнкция -это новый предикат, который принимает значение ложно при тех и только тех значениях из вещественной области, при которых оба предиката и ложны одновременно, и истинно во всех других случаях.

Отрицание предиката - это новый предикат, который принимает значение истинно при всех из вещественной области, при которых предикат принимает значение ложно и наоборот.

Квантовые операции.

Для предикатов кроме логических операций применимы кванторные операции: всеобщности и существования.

Пусть - предикат, определенный на множестве . Тогда - означает «для всякого (любого) истинно ». Символназываетсяквантором всеобщности.

Переменную в предикате называютсвободной ( ей можно придавать различные значения из М), в высказывании переменную называют связанной квантором всеобщности.

Пусть - предикат, определенный на множестве . Тогда - означает «существует ,для которого истинно ». Символназываетсяквантором существования.

ПРИМЕР

Пусть на множестве натуральных чисел задан предикат -«число кратно 3». Используя кванторы, из данного предиката можно получить высказывания:

- «все натуральные числа кратны 3»;

- «существуют натуральные числа, кратные 3».

Очевидно, что первое из данных высказываний ложно, а второе – истинно.

Кванторные операции применяются и к многоместным предикатам. Пусть на множестве задан двухместный предикат. К данному предикату могут применяться кванторные операции как по одной, так и по двум переменным.

ПРИМЕР

Пусть предикат означаетделится набез остатка., причем обе переменные определены на множестве натуральных чисел. Тогда применение кванторных операций приводит к следующим высказываниям:

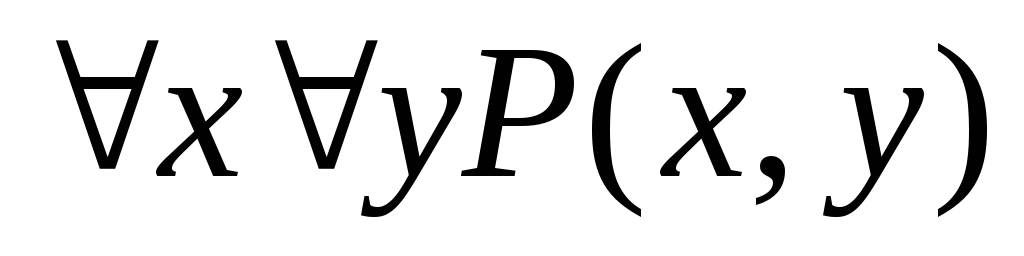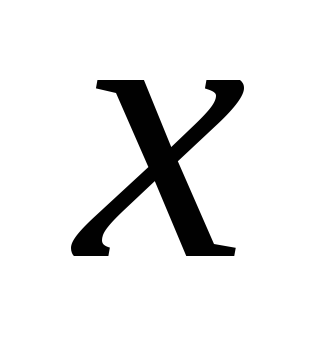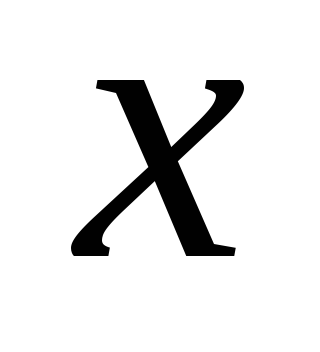1. - «для любого и для любогосправедливо, чтоделится набез остатка.

2. - «для любого 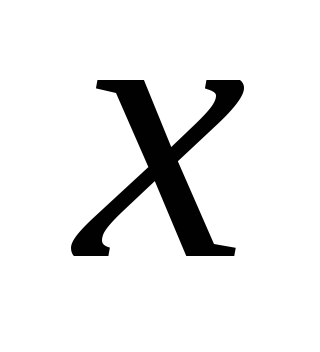существует, который является делителем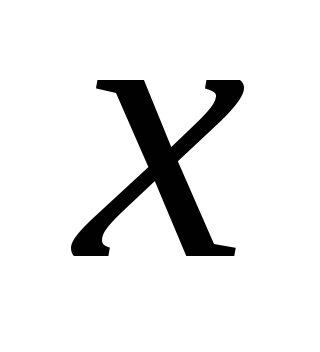без остатка.

Нетрудно заметить, что первое высказывание является ложным, а второе – истинным.

Для многоместных предикатов, связанных по одной переменной справедливы следующие формулы:

,

где

,

где

Равносильные формулы логики предикатов.

Две формулы логики предикатов иназываютсяравносильными на области,если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области .

Две формулы логики предикатов иназываютсяравносильными, если они равносильны во всякой области.

Очевидно, что все формулы равносильности алгебры высказываний будут верны, если в них вместо переменных подставить формулы логики предикатов. Но , кроме того, имеют место равносильности самой логики предикатов:

Закон де Моргана:

1. 

2. 

Закон двойного отрицания:

3. 

4. 

5. 

6. 

7. 

Для произвольного высказывания (предиката, не связанного по переменной) справедливы следующие формулы равносильности:

8. 

9. 

10. 

11. 

12. 

13. 

Формулы замены переменных (где ииз одной предметной области):

14. 

15.