Вопрос 16.Момент силы относительно точки

Одним из основных понятий механики наряду с моментом пары является понятие момента силы относительно данной точки. С этим понятием мы уже встречались при рассмотрении равновесия рычага.

Во всех задачах статики, относящихся к плоской системе сил, мы будем рассматривать момент силы как величину алгебраическую. Момент силы относительно данной точки положительный, если сила направлена относительно этой точки против движения часовой стрелки, и отрицательный, если сила направлена по движению часовой стрелки.

Абсолютное значение момента силы относительно данной точки равно произведению модуля силы на ее плечо (длину перпендикуляра, опущенного из этой точки на линию действия силы). Поэтому для силы F на рис.5.1 момент равен .

Рис.5.1. Рис.5.2.

В случае на рис.5.2 момент силы равен 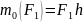Из рисунков видно, что абсолютное значение момента силы F относительно точки О численно равно двойной площади треугольника ОАВ, так как отрезок АВ=F является основанием этого треугольника, а плечо h – высотой. Точно также момент силы F₁ относительно точки О численно равен удвоенной площади треугольника ОА₁В₁.

Из данного определения момента силы следует:

1. Момент силы относительно данной точки на изменяется при переносе точки приложения силы по линии ее действия.

2. Момент силы относительно данной точки обращается в нуль в том случае, когда линия действия силы проходит через эту точку, так как в этом случае плечо силы равно нулю.

3. Сумма моментов двух равных по модулю сил, направленных по одной прямой в противоположные стороны, относительно любой точки равна нулю, так как моменты таких сил равны по абсолютной величине, но противоположны по знаку.

Вопрос 17.Приведение плоской системы сил к данному центру

Задача сложения плоской системы сил.

Пусть на данное тело действует плоская система сил F₁, F₂, F₃, …, F_n. Применяя способ последовательного сложения сил, такую систему можно привести или к одной равнодействующей силе, или к одной паре, если эта система сил не находится в равновесии.

Существует способ приведения плоской системы сил более эффективный, чем способ последовательного сложения сил, который называется приведением системы сил к данному центру. Он основан на следующей теореме:

Любая данная система сил эквивалентна по модулю и направлению силе, но приложенной в другой точке тела, и некоторой паре.

Доказательство. Пусть имеем силу F, приложенную к телу в точке А (рис.5.3).

Рис.5.3.

В произвольно выбранной точке В тела приложим две равные по модулю и противоположные по направлению силы F' и F'', действующие по прямой параллельной силе F, причем F'=F''=F. Согласно аксиоме 2 (лекция1) система трех сил F, F' и F'' эквивалентна данной силе F. Таким образом, данную силу F можно заменить равной ей силой F', приложенной в произвольно выбранной точке В, и парой (F,F''), что и требовалось доказать.

Эта теорема показывает, что данную силу можно переносить параллельно самой себе в любую точку тела с присоединением соответствующей пары. Поэтому пару (F,F''), получающуюся при переносе точки приложения силы F из точки А в точку В, называют присоединенной парой.

Момент присоединенной пары (F,F'') равен: 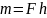, где h – плечо этой пары. С другой стороны, произведение Fh представляет собой момент силы F относительно точки В, следовательно,

Мы получили это равенство для случая, представленного на рисунке 5.3, когда сила F стремится вращать тело вокруг точки В против движения часовой стрелки, т.е. когда и момент присоединенной пары и момент силы F положительны. Очевидно, что это равенство будет иметь место в случае, когда момент силы F относительно точки В отрицателен.

Момент присоединенной пары (F,F'') равен (по абсолютной величине и знаку) моменту силы F относительно новой точки приложения силы.

Пусть имеем плоскую систему сил F₁, F₂ и F₃, приложенных соответственно в точках А₁, А₂, А₃ (рис.5.4). Возьмем в плоскости этих сил какую-нибудь точку О, называемую центром приведения, и, пользуясь предыдущей теоремой, перенесем точки приложения данных сил в точку О. Получим силы F'₁, F'₂ и F'₃ и соответствующие присоединенные пары (F₁,F₁''), (F₂,F₂'') и (F₃,F₃''). Силы F'₁, F'₂ и F'₃, как приложенные в одной точке О, мы можем сложить по правилу силового многоугольника. Получим равнодействующую R', приложенную к той же точке О и равную их векторной сумме: или , так как силы F'₁, F'₂ и F'₃ равны соответственно силам F₁, F₂ и F₃.

Рис.5.4.

Сложив пары (F₁,F₁''), (F₂,F₂'') и (F₃,F₃'') получим согласно теореме о сложении пар, лежащих в одной плоскости, одну равнодействующую пару, алгебраическую величину момента которой обозначим через М_О.

Так как при сложении пар, лежащих в одной плоскости, момент равнодействующей пары равен алгебраической сумме моментов слагаемых пар, то, обозначая алгебраическое значение момента присоединенной пары (F_i,F_i'') через m_i, будем иметь:

Момент присоединенной пары, получаемой при изменении точки приложения силы, равен моменту силы относительно ее новой точки приложения. Следовательно: , поэтому

Векторная сумма всех сил системы называется главным вектором данной системы сил:

Сумма моментов всех сил системы относительно какого-нибудь центра называется главным моментом системы сил относительно данного центра.

Плоскую систему сил в общем случае можно привести к одной силе, приложенной в произвольно выбранной точке и равной главному вектору данной системы сил: , и к одной паре, момент которой равен главному моменту данной системы сил относительно той же точки:

Важно заметить, что сила R', приложенная в точке О, не является равнодействующей данной системы сил F₁, F₂ и F₃, так как эта система не эквивалентна одной силе R'. Так как главный вектор равен геометрической сумме сил данной системы, ни модуль, ни его направление не зависят от выбора центра приведения. Если за центр приведения брать различные точки плоскости, то во всех этих точках главный вектор будет один и тот же по модулю и по направлению. Значение главного момента зависит от выбора центра приведения, так как с изменением центра приведения плечи данной системы, а, следовательно, их моменты изменяются. Каждой точке плоскости соответствует определенное значение главного момента. Поэтому, когда говорят о главном моменте данной системы сил, то всегда нужно указывать, к какому центру приведения относится этот момент.

Выведем формулы, определяющие модуль и направление главного вектора R'.

Проведем через центр О координатные оси Ох и Оу (рис.5.4). Проекции данных сил F_i на эти оси обозначим через Х_i и Y_i, а проекции силы R' обозначим через R'_х и R'_у. Из векторного равенства на основании теоремы о проекции суммы данных векторов имеем: ;

Отсюда находим:

Эта формула позволяет вычислить модуль главного вектора R'. Направление главного вектора определяется углом α между этим вектором и положительным направлением оси х. Этот угол находится по формулам:

,