Вопрос 6.Разложение силы

Задача о разложении данной силы на две или несколько составляющих может оказаться неопределенной, так как разложить данную силу на две и более составляющих, лежащих с ней в одной плоскости, можно бесчисленным множеством способов, путем построения сколько угодно параллелограммов для которых данная сила будет служит диагональю. Для того чтобы задача стала определенной необходимы некоторые дополнительные условия. Всего на плосоксти может быть два случая:

1. Разложить данную силу F на две силы по двум заданным направлениям, лежащим с ней в одной плоскости.

Для этого достаточно из конца вектора F провести прямые, параллельные данным прямым I и II (рис.2.5), до их пересечения с этими прямыми в точках В и С. Векторы 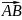и определяют искомые составляющие силы.

Рис.2.5.

2. Разложить данную силу F на две силы, лежащие с ней в одной плоскости и имеющие заданные численные значения.

Из начала А и конца В вектора F (рис.2.6) проводим две дуги радиусами, равными в выбранном масштабе заданными значениями F₁ и F₂ . Эти дуги пересекутся в точках С и D. Дополним треугольники АСВ и АDВ до соответствующих параллелограммов, в которых АВ является диагональю. Тогда векторы и или и 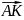определят искомые составляющие силы. Очевидно, что эта задача имеет два возможных решения.

Рис.2.6.

Разложение силы на три составляющих силы по трем заданным направлениям, не параллельным одной плоскости (например, по трем взаимно перпендикулярным координатным осям). Для этого на основании правила параллелепипеда, достаточно построить такой параллелепипед, ребра которого имели бы заданные направления и, диагональю которого являлась бы данная сила (рис.2.3)

Вопрос 7.Проекция вектора на ось

Пусть имеем вектор 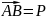и некоторую ось х. Проведем через начало и конец вектора плоскости, перпендикулярные к оси х и пересекающие эту ось в точках а и b (рис.2.7). Эти точки называются проекциями точек А и В на ось х, а длина отрезка аb, взятая с соответствующим знаком, называется проекцией вектора на ту же ось. Проекция вектора на ось представляет собой алгебраическую скалярную величину; ей приписывается знак +если направление вектора совпадает с направлением данной оси, в противном случае проекция отрицательна:

пр_хР=Р_х=аb

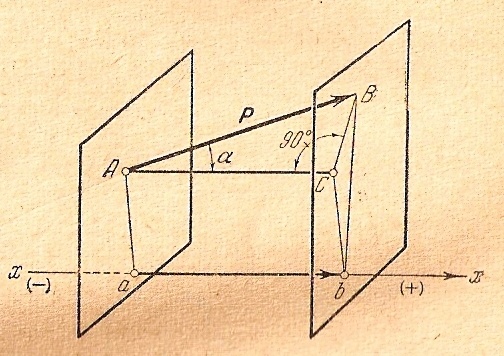Рис.2.7.

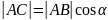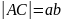Проведем через точку А начала вектора Р прямую, параллельную оси проекций; эта прямая пересечет плоскость Вb в точке С. Так как прямая АС перпендикулярна плоскости Вb, то в треугольнике АВС угол С прямой; угол ВАС=α – угол между вектором Р и положительным направлением оси проекций. Из треугольника АВС получаем: , т.к. , то

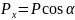
Полученное выражение для проекции вектора на ось определяет не только абсолютную величину, но и знак проекции. В рассматриваемом случае проекция Р_х положительна, а угол α – острый; следовательно, его косинус также положительный. В случае отрицательной проекции (рис.2.8) из треугольника А₁В₁С₁ имеем:

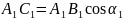
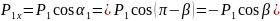
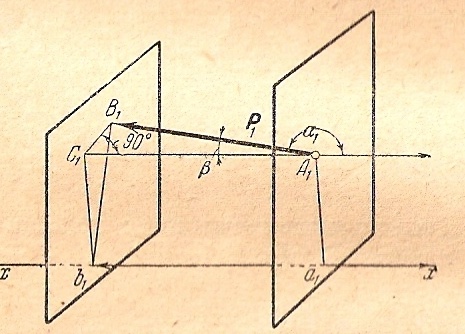Рис.2.8.

Проекция вектора на ось равна (по абсолютной величине и по знаку) произведению модуля вектора на косинус угла между этим вектором и положительным направлением оси проекций.

Из определения проекции вектора на ось следует, что проекция не изменится, если мы будем переносить вектор параллельно самому себе или если будем проектировать его на различные, но параллельные и одинаково направленные оси.

Возьмем прямоугольную систему координат О хуz и некоторый вектор рис.2.9.

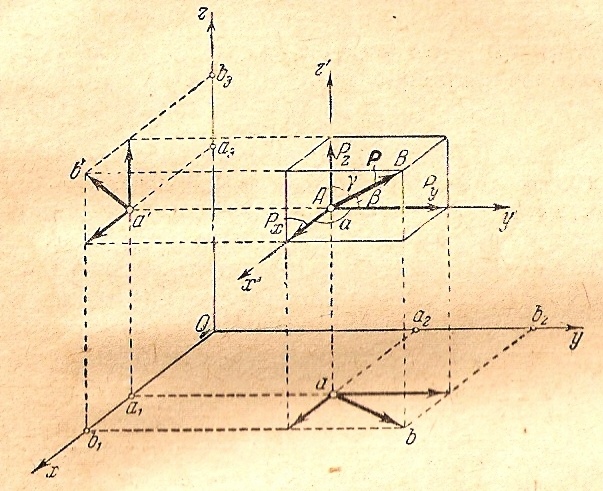Рис.2.9.

Проведем через точку А оси Ах', Ау' и Аz', параллельные данным координатным осям, и построим на новых осях прямоугольный параллелепипед, для которого вектор является диагональю. Длины выходящих из вершины А ребер этого параллелепипеда, взятые с соответствующими знаками, представляют собой проекции вектора на оси Ах', Ау' и Аz', или, что одно и то же, на оси Ох, Оу и Оz. Обозначая эти проекции через Р_х, Р_у и Р_z получим 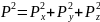, откуда 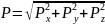(2.3)

Обозначим углы вектора Р с координатными осями х, у, z соответственно через α, β и γ, будем иметь: , 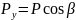, 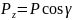(2.4)

Откуда

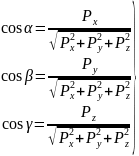(2.5)

Формулы (2.3) и (2.5) позволяют аналитически определить величину и направление вектора по трем заданным его проекциям на координатные оси. В этих формулах перед радикалами необходимо брать знак +, так как модуль вектора – величина положительная.