Вопрос 14. Момент пары

Парой сил называется система двух равных по модулю антипараллельных сил. Пара сил не имеет равнодействующей, т.е. пару сил нельзя заменить одной силой, ей эквивалентной. Поэтому в статике наряду со свойствами сил, действующих на тело, необходимо рассматривать и свойства пар. Теория пар позволяет вывести условия равновесия системы сил, приложенных к твердому телу в самом общем случае.

Расстояние между линиями действия сил пары (F, F'), т.е. длина перпендикуляра d, опущенного из точки приложения А одной из сил пары на линию действия второй силы, называется плечом пары (рис.3.1)

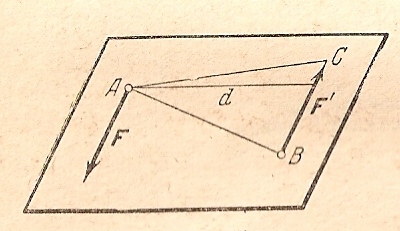Рис.3.1.

Плоскость, в которой расположена данная пара, называется плоскостью действия этой пары.

Численное значение момента пары определяется как произведение модуля одной из сил пары на плечо этой пары.

Численное значение момента пары будем обозначать через m:

Из рисунка 3.1 следует, что момент пары численно равен удвоенной площади треугольника АВС, т.е. треугольника, который получим соединив начало и конец одной из сил пары с точкой приложения второй силы.

Вопрос 15. Эквивалентные пары. Момент пары как вектор

Теорема 1. Две пары, лежащие в одной плоскости и имеющие численно равные моменты и одинаковое направление вращения, эквивалентны.

Доказательство: Пусть даны две пары (F, F') и (F₁, F₁'), лежащие в одной плоскости (рис.3.2), имеющие численно равные моменты и одинаковое направление вращения.

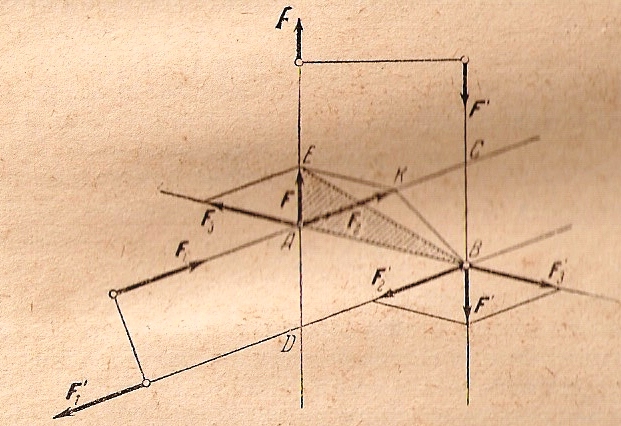Рис.3.2.

Обозначим точки пересечения линий действия сил двух данных пар через А, В, С и D и плечи данных пар d и d₁, то из условия равенства моментов пар имеем

Перенесем точку приложения силы F в точку А, точку приложения силы F' в точку В. Разложив силу F по направлениям АС и ВА, получим две силы F₂ и F₃. Аналогично разложив силу F' по направлениям ВD и АВ, получим силы F'₂ и F'₃.

В силовых треугольниках, которые получились при разложении сил F и F', углы попарно равны как углы с параллельными сторонами; кроме того, F=F', следовательно, эти треугольники равны, поэтому F₂=F'₂ и F₃=F'₃. Силы F₃ и F'₃ как равные по модулю и противоположные по направлению уравновешиваются. Остаются только силы F₂ и F'₂, образующие пару. Следовательно, вместо данной пары (F, F') получена новая пара эквивалентная ей (F₂, F'₂). Эти пары имеют равные моменты, так как момент пары (F, F') выражается удвоенной площадью треугольника АЕВ, а момент пары (F₂, F'₂) равен удвоенной площади треугольника АКВ. Но эти треугольники имеют равную площадь так, как у них общее основание АВ, а вершины Е и К лежат на прямой параллельной основанию. Обозначим моменты пар (F, F') и (F₂, F'₂) соответственно через m и m₂, поэтому m=m₂.

С другой стороны m(F, F')= и m₂(F₂, F'₂)= F₂d₂, поэтому , но по условию теоремы . Таким образом, силы F₂ и F₁ имеют равные модули и направлены по одной прямой в одну и ту же сторону. То же относится к силам F'₂ и F'₁. Отсюда, следует, что пары (F, F') и (F₁, F₁') эквивалентны.

Доказанная теорема дает условие эквивалентности пар, лежащих в одной плоскости.

Следствия:

1. Данную пару, не изменяя ее действие на тело, можно переносить в ее плоскости. Действие пары на тело не зависит от положения пары на плоскости.

2. Не изменяя действия данной пары на тело, можно изменять модуль сил и плечо этой пары, но при условии, чтобы момент и направление вращения оставались неизменными.

3. Две данные пары всегда можно привести к одному плечу, т.е. две или несколько пар можно заменить эквивалентными им парами, имеющими равные плечи.

Теорема 2. Данную пару, не изменяя ее действия на тело, можно переносить в любую плоскость, параллельную плоскости этой пары.

Доказательство. Пусть данная пара (F, F') лежит в плоскости I (рис.3.2).

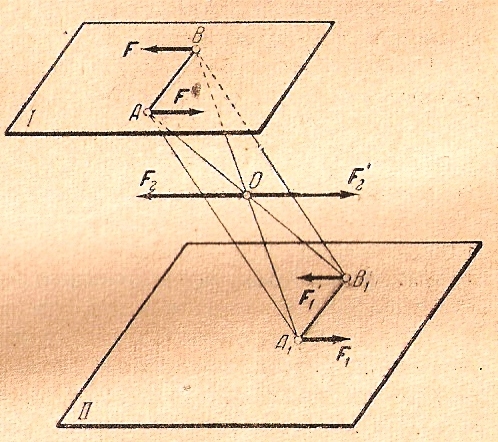Рис.3.2.

Проведем плоскость II параллельную плоскости I, и возьмем где нибудь в этой плоскости отрезок А₁В₁, равный и параллельный отрезку АВ. Соединив точку А с точкой А₁ и точку В с точкой В₁, получим параллелограмм АВА₁В₁. Точку пересечения диагоналей этого параллелограмма обозначим через О. Разложим силу F' на две параллельные ей составляющие силы, приложенные в точках О и В₁. Так как точка А лежит вне отрезка ОВ₁, то эти составляющие силы должны быть антипараллельны. В точке О будет приложена большая составляющая F'₂, имеющая то же направление, что и сила F'. В точке В₁ будет приложена меньшая составляющая F'₁, имеющая противоположное направление. Модуль силы F' равен разности модулей этих составляющих:

Так как расстояние АВ₁ вдвое больше расстояния АО, то . Отсюда можно найти модули обеих составляющих

Итак, силу F' мы заменили двумя эквивалентными силами F'₂ и F'₁. Аналогично заменим силу F данной пары на силы F₂ и F₁. При этом

Но так как F=F', то F₂=F'₂ и F₁=F'₁. Отсюда видно, что силы F₂ и F'₂, как равные по модулю уравновешиваются, а потому остаются только две силы F₁ и F'₁, образующие пару. Поэтому вместо данной пары (F, F') получим эквивалентную ей пару (F₁, F₁'), которая представляет собой ту же пару, перенесенную в плоскость II.

Так как перпендикуляры к параллельным плоскостям имеют одинаковое направление, то из этой теоремы следует, что действие пары на тело не зависит от положения пары на плоскости, а зависит только от направления перпендикуляра к этой плоскости. Соединяя результаты, полученные на основании доказанных теорем 1 и 2, мы видим, что действие пары на тело определяется следующими факторами:1 Численным значением момента пары; 2Направлением перпендикуляра к плоскости действия пары; 3 Направлением вращения пары

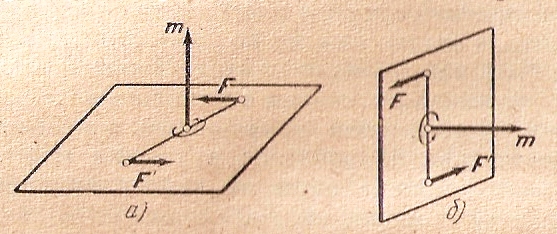Рис.3.3.