Вопрос 70. Относительное удлинение и угол сдвига

Деформацией называется такое изменение положений точек тела, при котором изменяются расстояния между любыми двумя его точками.

Деформация возникает вследствие нагрузки тела или вследствие изменения температуры. Изменение положений точек тела может привести к изменению длин и к изменению углов в теле. В первом случае возникает линейная деформация, а во втором угловая деформация. Линейная деформация измеряется относительным удлинением, а угловая деформация – углом сдвига.

Относительное удлинение.

Рассмотрим стержень, на котором сделаны две отметки на расстоянии друг от друга. Приложим к стержню растягивающую нагрузку (рис.1)

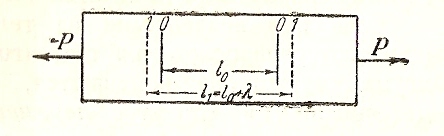Рис.1.

Расстояние между отметками увеличится и сделается равным

Найдем отношение

Т.е. отношение изменения длины к первоначальной длине называется относительным удлинением. Относительное удлинение является безразмерной величиной.

Угол сдвига. Плоское напряженное состояние, при котором на двух парах взаимно перпендикулярных плоскостей имеются только касательные напряжения, называется чистым сдвигом. Возьмем частицу в форме прямоугольного параллелепипеда и закрепим неподвижно ее основание (рис.2). Подвергнем параллелепипед чистому сдвигу. Его углы из прямых сделаются косыми.

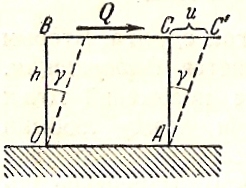Рис.2

Величина , на которую изменился первоначально прямой угол, называется углом сдвига. Так как при малых углах можно принять, что , то из рисунка видно, что:

При рассмотрении этих примеров мы сделали два важных допущения. Было принято, что нормальные напряжения связаны только с линейными деформациями, а касательные напряжения только с угловыми деформациями. Это допущение справедливо только для малых деформаций и на нем основана линейная теория упругости.

Если при воздействии на тело внешних сил его точки изменяют свои положения так, что расстояния между любыми его двумя точками не изменяются, то мы будем иметь не деформацию, а жесткое перемещение тела. В этом случае тело не деформируется, а изменяет свое положение так, как если бы оно было абсолютно твердое.

Вопрос 71. Компоненты тензора деформации

Формулы относительного удлинения и сдвига применимы к конечным по размерам частям тела только в случае, если в этих частях тела относительное удлинение и угол сдвига одинаковы для всех отрезков во всех плоскостях. В общем случае относительное удлинение и угол сдвига изменяются при переходе от одной точки к другой.

Рассмотрим деформацию тела в общем случае. Для этого выделим внутри тела элементарный объем в виде прямоугольного параллелепипеда с ребрами . Деформация этого параллелепипеда будет известна, если будут заданы изменения длин трех его ребер и изменения трех его углов, образуемых каждой парой ребер, сходящихся в общей вершине. Изменения длин ребер, разделенные на первоначальные длины, называются относительными удлинениями по направлениям x, y, z и обозначаются соответственно через . Изменения первоначально прямых углов, образованных каждой парой ребер, сходящихся в общей вершине, называются углами сдвига в плоскостях yz, zx, xy и обозначаются соответственно .

Шесть величин , называются компонентами тензора деформации, и характеризуют деформацию в точке, в которую стягивается параллелепипед при переходе к пределам .

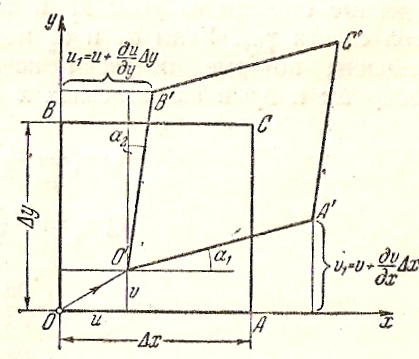Рис.3

Положению каждой точки в недеформированном состоянии соответствует определенной положение той же точки в деформированном параллелепипеде. Пусть точка О в результате деформации перешла в положение О’ (рис.3). Вектор будем называть вектором перемещений (перемещением) точки О. Покажем, что шесть компонентов тензора деформации в точке О можно выразить через производные от компонентов u, v, w вектора перемещения точки О по координатам x, y, z. При этом будем предполагать, что перемещение и его компоненты u, v, w по направлениям, совпадающим с ребрами параллелепипеда, являются непрерывными и дифференцируемыми функциями.

Пусть компонент перемещения начальной точки О ребра в направлении х равен u, тогда компонентом перемещения точки А этого ребра в том же направлении будет: ; ;

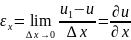
Относительным удлинением в направлении оси х будет предел отношения изменения длины ребра в направлении оси х к первоначальной длине ребра. Аналогично, можно определить относительные удлинения в двух других направлениях.

Изменение первоначального угла между ребрами и , определяющее угол сдвига , происходит вследствие того, что грани ОА и ОВ поворачиваются при деформации в разные стороны на углы и , в сумме составляющие угол сдвига . Углы и можно выразить через перемещения, которые получают начальная и конечная точки ребер и . ;

Где ;

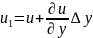
В случае малых деформаций 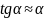, и поэтому для угла сдвига в плоскости х у получим выражение:

Аналогично, можно получить выражения для углов сдвига и .

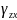Таким образом, мы получаем для шести компонентов тензора деформации следующие выражения:

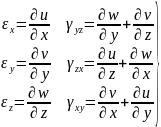
Компоненты тензора деформации выражаются через первые частные производные от трех перемещений u, v, w по координатам x,y,z. Полученные равенства называют соотношениями Коши.

Мы можем говорить о деформации тела только в том случае, если происходит относительные перемещения точек друг относительно друга. Но относительные перемещения точек тела не изменяются, если расстояния между ними остаются постоянными, т.е. при жестком перемещении. Поэтому любая деформация может быть определена с точностью до жесткого перемещения.

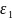При трехосном деформированном состоянии в каждой точке тела имеются три взаимно перпендикулярные оси, углы между которыми не изменяются при деформации. Следовательно, для плоскостей, определяемых этими осями углы сдвига , , равны нулю и вся деформация определяется только относительными удлинениями , , . Относительные удлинения , , называют главными относительными удлинениями, а соответствующие им оси – главными осями деформации.

В теории упругости показано, что в каждой точке изотропного тела главные направления напряжений совпадают с главными осями деформаций.