
- •Вопрос 1. Абсолютно твердое тело. Материальная точка. Система отсчета.
- •Вопрос 2. Понятие силы
- •Вопрос 3. Аксиомы статики
- •Вопрос 4. Связи и реакции связей
- •Вопрос 5.Сложение сил, приложенных в одной точке
- •Вопрос 6.Разложение силы
- •Вопрос 7.Проекция вектора на ось
- •Вопрос 8.Умножение вектора на скаляр. Единичный вектор
- •Вопрос 9. Разложение вектора по координатным осям
- •Вопрос 10.Аналитический способ сложения сил
- •11.Равновесие системы сходящихся сил
- •Вопрос 12.Момент силы относительно точки. Условие равновесия рычага
- •Вопрос 14. Момент пары
- •Вопрос 15. Эквивалентные пары. Момент пары как вектор
- •Вопрос 16.Момент силы относительно точки
- •Вопрос 17.Приведение плоской системы сил к данному центру
- •18.Равнодействующая плоской системы сил. Теорема Вариньона
- •Вопрос 19. Приведения плоской системы сил к одной паре
- •Вопрос 20. . Условия равновесия плоской системы сил
- •Вопрос 21. . Равновесие системы, состоящей из нескольких твердых тел
- •Вопрос 22. Трение скольжения
- •Вопрос 23. Трение качения
- •Вопрос 24. Момент силы относительно оси
- •Вопрос 25. Формулы для моментов силы относительно координатных осей
- •26.Момент силы относительно точки как вектор
- •Вопрос 29. Равнодействующая системы сил. Теорема Вариньона
- •Вопрос 30. Условия равновесия системы сил в общем случае
- •Вопрос 31. Равновесие несвободного тела
- •Вопрос 32. Общие формулы для координат центра тяжести
- •Вопрос 33. Положение центра тяжести симметричного тела
- •Вопрос 34. Уравнение движения точки и график движения
- •Вопрос 35. Определение пути, пройденного точкой, по заданному закону изменения ее скорости
- •Вопрос 36. Скорость точки в криволинейном движении
- •Вопрос 37. Ускорение точки в криволинейном движении
- •Вопрос 38. Определение скорости и ускорения из уравнений движения точки в декартовых координатах
- •Вопрос 39. Проекция ускорения на естественные оси. Касательное и нормальное ускорения
- •Вопрос 40. Поступательное движение твердого тела
- •Вопрос 41. Вращение твердого тела вокруг неподвижной оси
- •Вопрос 42. Угловая скорость как вектор. Выражение линейной скорости и касательного и нормального ускорений в виде векторных произведений
- •Вопрос 43.Сложное движение точки. Относительное, переносное и абсолютные движения
- •Вопрос 44. Относительные, переносные и абсолютные скорость и ускорение точки
- •Вопрос 45. Уравнения плоскопараллельного движения твердого тела
- •Вопрос 46.Разложение движения плоской фигуры на поступательное и вращательное
- •Вопрос 47. Уравнения движения свободного тела в общем случае. Разложение движения твердого тела на поступательное движение и движение вокруг некоторой точки.
- •Вопрос 48. Основные законы динамики.
- •Вопрос 49 . Дифференциальные уравнения движения материальной точки
- •18.3. Две основные задачи динамики точки
- •Вопрос 50. Дифференциальное уравнение прямолинейного движения точки
- •Вопрос 51. Прямолинейное Движение точки под действием силы.
- •Вопрос 52.Теорема о количестве движения
- •Вопрос 53. Теорема о моменте количества движения
- •Вопрос 54. Работа
- •Вопрос 55. Теорема о кинетической энергии материальной точки
- •Вопрос 57. Понятие о потенциальной энергии
- •Вопрос 58. Закон сохранения механической энергии
- •Вопрос 59. Принцип Даламбера для материальной точки.
- •Вопрос 60. Цели и задачи сопротивления материалов
- •Вопрос 61. Внешние и внутренние силы
- •Вопрос 62. Нормальные и касательные напряжения
- •Вопрос 63. Линейное (одноосное) напряженное состояние
- •Вопрос 64. Плоское (двухосное) напряженное состояние
- •Вопрос 65. Главные напряжения
- •Вопрос 68 Круги Мора для трехосного напряженного состояния
- •Вопрос 70. Относительное удлинение и угол сдвига
- •Вопрос 71. Компоненты тензора деформации
- •Вопрос72. Относительное объемное расширение
- •Вопрос 73. Условия совместности деформаций
- •Вопрос 78. Поперечное сжатие. Коэффициент Пуассона.
- •Вопрос 79 и 80. Предел текучести, течение материала, упрочнение, разрыв.
- •Вопрос 81. Предел упругости
- •Вопрос 82. Сжатие стального образца
- •Вопрос 83. Растяжение сжатие других технически важных материалов
- •Вопрос 84. Твердость
- •Вопрос 85. Переменная нагрузка
- •Вопрос 88. Закон Гука в общей форме
- •Вопрос 89. Теории прочности
- •Вопрос 90. Закон Гука для сдвига. Модуль сдвига
Вопрос 65. Главные напряжения
Найдем, при каких углах φ получаются экстремальные значения σ. Для этого найдем производную σ по φ и приравняем ее к нулю:
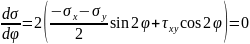
Обозначим
значение угла φ, удовлетворяющее этому
уравнению через φ0.
Тогда:
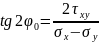
На
круге напряжений Мора угол
 получается при центре М построением
прямоугольного треугольника по заданным
катетам
и
.
получается при центре М построением
прямоугольного треугольника по заданным
катетам
и
.
Подставляя
в полученную формулу угол
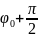 ,
получим, что
,
получим, что
 .
Следовательно, существуют две взаимно
перпендикулярные плоскости, для которых
нормальное напряжение принимает
экстремальные значения. Эти плоскости
называются главными
плоскостями напряжений,
а действующие в них нормальные напряжения
– главными
напряжениями.
Из второго уравнения системы σ, τ,:
следует, что в главных плоскостях
касательные напряжения равны нулю.
.
Следовательно, существуют две взаимно
перпендикулярные плоскости, для которых
нормальное напряжение принимает
экстремальные значения. Эти плоскости
называются главными
плоскостями напряжений,
а действующие в них нормальные напряжения
– главными
напряжениями.
Из второго уравнения системы σ, τ,:
следует, что в главных плоскостях
касательные напряжения равны нулю.
Величину
главных напряжений
 и
и
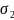 можно определить из круга Мора (рис.7)
или из уравнения:
можно определить из круга Мора (рис.7)
или из уравнения:
Если
положить в нем
 ,
получим:
,
получим:

Аналогичным
способом определяются углы
 ,
которым соответствуют экстремальные
значения касательного напряжения:
,
которым соответствуют экстремальные
значения касательного напряжения:
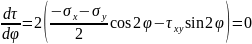
Откуда
получаем:

Очевидно,
что
 ,
следовательно:
,
следовательно:
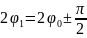
Или

Таким
образом, существуют два направления,
для которых касательные напряжения
получают свои экстремальные значения
( .
Эти направления делят пополам углы
между главными напряжениями.
.
Эти направления делят пополам углы
между главными напряжениями.
Из
уравнения
и
,
получим, что
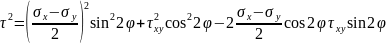
И
 Откуда
Откуда

Т.е.
Экстремальные касательные напряжения
равны друг другу по абсолютному значению,
но противоположны по знаку. Очевидно,
что
 численно равны радиусу круга напряжений
Мора.
численно равны радиусу круга напряжений
Мора.
Если
площадки ВС и СА являются плоскостями
главных напряжений
и
(рис.8), тогда будем иметь:
,
 ,
,

И выражения напряжений σ и τ в произвольном сечении примут более простой вид:
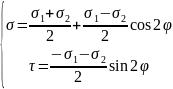
Уравнением
окружности, ограничивающей круг
напряжений Мора, будет:
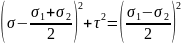
Абсолютная
величина экстремальных касательных
напряжений равна: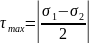
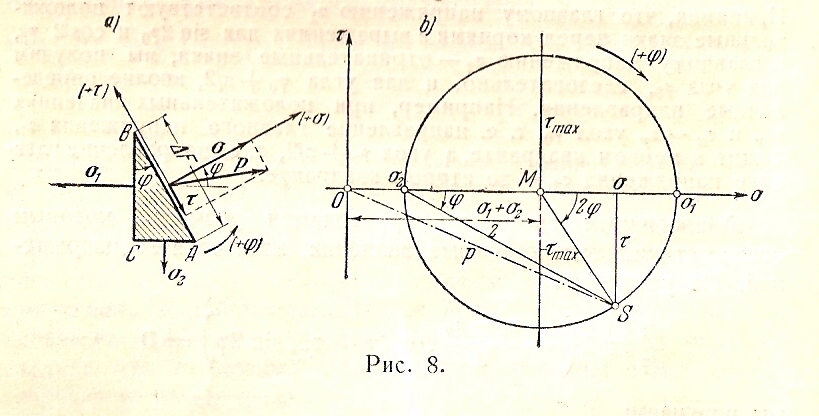
Для
построения круга Мора по заданным
напряжениям
и
,
следует отложить на оси σ
от точки О отрезки
 и
и
 (рис.8) и на отрезке
(рис.8) и на отрезке
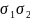 ,
как на диаметре построить окружность.
Для определения напряжений σ
и τ
в сечении, образующем угол φ с плоскостью
главного напряжения
,
следует построить в центре круга угол
,
как на диаметре построить окружность.
Для определения напряжений σ
и τ
в сечении, образующем угол φ с плоскостью
главного напряжения
,
следует построить в центре круга угол
 .
Тогда координаты σ
и τ
точки S
и будут искомыми напряжениями.
.
Тогда координаты σ
и τ
точки S
и будут искомыми напряжениями.
Вопрос 66 и 67- убрали… =)
Вопрос 68 Круги Мора для трехосного напряженного состояния
Трехосное
напряженное состояние можно изобразить
в плоскости при помощи построения,
состоящего из трех кругов, которые
называются кругами напряжений Мора
(рис.10). Пусть напряженное состояние
задано главными напряжениями
,
,
 .
.
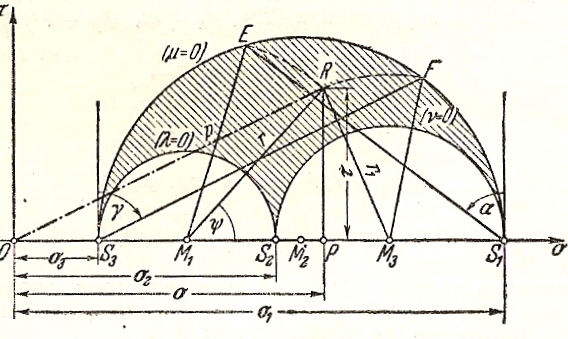 Рис.10
Рис.10
Отложим
на оси σ отрезки
 ,
,
 ,
,
 и построим на отрезках
и построим на отрезках
 ,
,
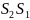 ,
,
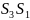 ,
как на диаметрах, полуокружности. Эти
полуокружности ограничивают заштрихованный
на рис.10 треугольник, сторонами которого
являются дуги окружностей. Все напряжения,
возможные при заданном напряженном
состоянии, изображаются координатами
σ, τ точек, лежащих внутри или на сторонах
заштрихованного треугольника.
,
как на диаметрах, полуокружности. Эти
полуокружности ограничивают заштрихованный
на рис.10 треугольник, сторонами которого
являются дуги окружностей. Все напряжения,
возможные при заданном напряженном
состоянии, изображаются координатами
σ, τ точек, лежащих внутри или на сторонах
заштрихованного треугольника.
Для
того, чтобы найти напряжения σ и τ,
соответствующие площадке, нормаль к
которой образует с осями углы α, β, γ,
следует отложить при
 угол
,
при
угол
,
при
 угол
угол
 ,
причем тот и другой углы следует
отсчитывать от перпендикуляров к оси
в точках
и
.
Пусть наклонные стороны углов
и
пересекают внешнюю окружность в точках
Е и F.
Опишем из центра М1
дугу ЕR
радиусом М1Е,
а из центра М3
– дугу FR
радиусом М3F.
Координаты точки R
пересечения этих дуг дадут значения
нормального напряжения
и касательного напряжения
на взятой элементарной площадке.
Абсолютная величина наибольшего из
всех возможных касательных напряжений
равна радиусу внешней окружности, т.е.
,
причем тот и другой углы следует
отсчитывать от перпендикуляров к оси
в точках
и
.
Пусть наклонные стороны углов
и
пересекают внешнюю окружность в точках
Е и F.
Опишем из центра М1
дугу ЕR
радиусом М1Е,
а из центра М3
– дугу FR
радиусом М3F.
Координаты точки R
пересечения этих дуг дадут значения
нормального напряжения
и касательного напряжения
на взятой элементарной площадке.
Абсолютная величина наибольшего из
всех возможных касательных напряжений
равна радиусу внешней окружности, т.е.
 .
.
Вопрос 69. Убрали =)
