Вопрос 63. Линейное (одноосное) напряженное состояние

Согласно сказанному выше, можно говорить о напряжении только в сочетании с той элементарной площадкой, на которой действует напряжение. Совокупность напряжений на всех элементарных площадках, которые можно провести через какую-либо точку тела, называется напряженным состоянием в данной точке.

Рассмотрим линейное или одноосное напряженное состояние, отличительным признаком которого является одинаковое направление векторов всех полных напряжений. Такое напряженное состояние имеет место при растяжении стержня двумя противоположными силами. Выше мы определили напряжения только в сечении, нормальном к оси стержня. Определим напряжения во всех косых сечениях s - s, пересекающих ось стержня и имеющих общую точку s с сечением s – s’, перпендикулярным к оси стержня (рис.4а)

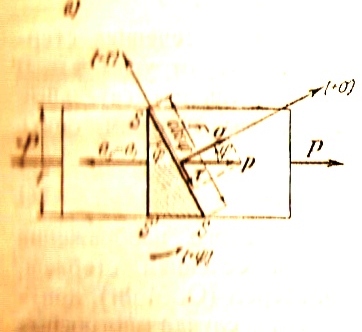Рис.4.

Обозначим нормальное напряжение, действующее в сечении s – s’, перпендикулярном к оси стержня, через 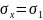. Оно будет равно:

Полное напряжение , действующее в косом сечении разложим на нормальную и касательные составляющие. Для того, чтобы заштрихованный участок стержня находился в равновесии, необходимо, чтобы напряжение было равно по направлению нормальному напряжению . Площадь косого сечения s – s равна . Следовательно, из условия равновесия заштрихованной призмы в направлении, параллельном оси стержня мы получим:

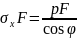
Откуда

Проектируя на нормаль к сечению s – s, можно определить значения нормального и касательного напряжений.

Установим положительное направление в плоскости сечения s – s. Нормальное напряжение считается положительным, если оно направлено наружу от рассматриваемого элемента поверхности.

Угол φ, определяющий положение косого сечения s – s, будем считать положительным, если для перевода сечения s – s’, перпендикулярного к оси стержня, в положение s – s по кратчайшему пути, надо его повернуть против часовой стрелки. Соответственно будем считать положительным направлением для касательных напряжений, то направление, которое получается поворотом нормали к сечению s – s на 90 против часовой стрелки.

Выполняя разложение напряжения на нормальное и касательное напряжение, получим: ;

Очевидно, что во всех сечениях стержня за исключением тех, которым соответствуют углы 0 и 90, имеют место как нормальные, так и касательные напряжения. Сложив напряжения и , мы получим равенство:

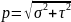
Существует простой способ графического изображения напряжений, соответствующих разным сечениям стержня. Он был впервые предложен О. Мором и допускает обобщение на случай многоосных напряженных состояний.

Возьмем прямоугольную систему координат и (рис.5) и будем откладывать в ней значения и , соответствующие определенному углу φ, как координаты точки S. Эта точка будет служить изображением полного напряжения в сечении, проведенном под углом φ.

Очевидно, что все точки соответствующие всем возможным значениям угла φ, расположены на окружности, имеющий центр на оси и проходящий через начало координат О.

Преобразуем значения нормального и касательного напряжения в виде: ;

Исключив из этих уравнений параметр φ, получим уравнение геометрического места точек S: ;

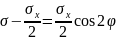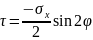
Откуда

Т.е. это геометрическое место будет собой представлять окружность с радиусом равным

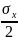
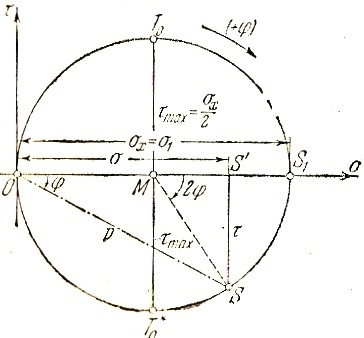Рис.5. Круговая диаграмма Мора.

Круг, ограниченный этой окружностью, называется круговой диаграммой Мора для рассматриваемого одноосного напряженного состояния.

Напряжения и , соответствующие любому углу φ, т.е. любому сечению стержня, определяются абсциссой и ординатой точки S, лежащей на окружности круговой диаграммы напряжений Мора.

Далее из этих уравнений получим:

Координаты точки S равны , . Тогда угол , a .

Следовательно, зная напряжения и , можно найти угол , определяющий наклон сечения, в котором действует напряжение с компонентами и

При пользовании круговой диаграммой Мора необходимо иметь в виду следующее обстоятельство. На схеме напряжений рис.4 мы приняли за положительное направление отсчета углов φ направление вращения против часовой стрелки. В круге Мора с целью установления однозначного соответствия между напряжениями и точками круга необходимо поступать наоборот, т.е. положительные углы φ отсчитывать по часовой стрелке.

Такое положение можно было бы избежать, откладывая касательные напряжения в направлении вниз (изменив их знак на обратный). Но такое изображение касательных напряжений нецелесообразно.

Из рис.5 видно, что наибольшие значения, которые может принимать касательное напряжение, равны:

Этим значениям соответствуют углы или . Следовательно, наибольшие касательные напряжения возникают в сечениях, наклоненных, к оси стержня на углы .

В предыдущих рассуждениях мы допускали, что напряжения одинаковы во всех точках конечного по размерам сечения. Такое напряженное состояние называется однородным. В общем случае напряжения в различных точках тела различны. Следовательно, они являются функциями положения точки в пространстве, и, поэтому, наши рассуждения надо применять не ко всему телу в целом, а к отдельным его элементам.