Вопрос 50. Дифференциальное уравнение прямолинейного движения точки

Пусть материальная точка описывает под действием силы прямолинейную траекторию. Примем эту прямую за ось х; координаты у и z остаются за все время движения равными нулю, то дифференциальные уравнения движения точки имеют вид:

, и

Из последних двух уравнений следует, что в прямолинейном движении точки направление действующей силы совпадает с направлением траектории и, следовательно, , причем знак плюс соответствует случаю, когда действующая сила направлена в положительную сторону оси х, а знак минус - противоположному направлению этой силы. Таким образом, в случае прямолинейного движения имеем лишь одно дифференциальное уравнение:

Рассмотрим, как определяется закон прямолинейного движения точки, когда действующая на нее сила известна. Пусть действующая на точку сила постоянна . В этом случае точка имеет постоянное ускорение, проекция которого на ось х равна:

Следовательно, движение точки является равномерно переменным. В этом случае скорость и пройденный точкой путь определяются по известным в кинематике соотношениям равномерного переменного движения.

При этом, если скорость по абсолютной величине возрастает, то движение называется равномерно ускоренным. Если скорость по абсолютной величине убывает, то движение называют равномерно замедленным. Из равенства имеем .

Интегрируя это уравнение в соответственных пределах, находим:

Или , где v₀ – начальная скорость точки.

Для определения пути S, пройденного точкой за время t при равномерно переменном движении, получим6:

Преобразуем эту формулу, вынеся за скобки множитель t/2:

Из формулы скорости получим

В случай переменной силы имеет три варианта:

1. Сила может изменяться по определенному закону с течением времени

2. Сила может зависеть от положения точки, определяемого ее координатой х

3. Сила может зависеть от скорости движущейся точки.

В самом общем случае действующая на точку переменная сила может зависеть одновременно от всех трех аргументов: времени t, координаты х и скорости :

В этом случае интегрирование данного уравнения представляет большие математические трудности. Общих методов интегрирования таких уравнений для произвольной функции не существует и, поэтому, приходится ограничиваться приближенными методами интегрирования.

Рассмотрим три основных частных случая:

1. Действующая на точку сила является только функцией времени;

2. Действующая сила является функцией только координаты х;

3. Действующая на точку сила является только функцией скорости .

Вопрос 51. Прямолинейное Движение точки под действием силы.

зависящей от времени

Пусть материальная точка массы движется по оси х под действием переменной силы, зависящей от времени, т.е. . Так как:

и , то дифференциальное движения точки мы можем написать в виде:

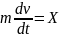или

Интегрируя это уравнение в соответствующих пределах, получим:

Так как функция известна, то последний интеграл можно вычислить, в результате чего мы получим некоторую функцию времени, которую обозначим через , т.е.:

Определяя отсюда , получим:

Это уравнение определяет скорость точки как функцию времени t. Заменяя здесь на , получим:

или

Пусть начальная абсцисса точки при равна . Тогда интегрируя это уравнение в пределах от до х и от 0 до , находим:

Или

Это уравнение, выражающее значение координаты х в функции от времени , представляет собой искомый закон прямолинейного движения точки под действием данной переменной силы, зависящей от времени.

Движение точки под действием силы, зависящей от положения точки

Пусть , где есть некоторая данная функция от абсциссы х движущейся точки. В этом случае для интегрирования дифференциального уравнения движения точки

Представим это уравнение в виде:

Заменяя через , получим:

Отсюда

Пусть и будут соответственно абсцисса и скорость точки в начальный момент времени . Интегрируя это уравнение в соответствующих пределах, получим:

Выполняя здесь интегрирование, получим некоторую новую функцию переменного х, которую обозначим через .

Из этого уравнения получаем:

Или

Эта формула определяет скорость точки как функцию ее абсциссы х.

Заменяя через и умножая обе части последнего равенства на dt, получим:

Разделяя переменные, будем иметь:

Интегрируя это уравнение в пределах от до х и от 0 до , получим:

Это уравнение устанавливает зависимость между х и . Выполнив интегрирование в левой части и решив полученное после этого уравнение относительно х, найдем уравнение движения точки в конечном виде: .

Движение точки под действием силы, зависящей от скорости

Пусть . В этом случае можно указать два способа интегрирования дифференциального уравнения движения точки.

1. Напишем дифференциальное уравнение движения в виде:

Разделяя переменные, получим:

Интегрируя это уравнение в пределах от до и от 0 до , получим:

Выполнив интегрирование и решив полученное после этого уравнение относительно , найдем скорость как некоторую функцию времени:

Отсюда вторичным интегрированием находим абсциссу х движущейся точки как функцию времени:

И, следовательно,

2. Напишем дифференциальное уравнение в виде:

Разделяя, переменные получим:

Интегрируя это уравнение в пределах, получим:

Выполнив интегрирование в левой части и решив затем полученное уравнение относительно , найдем скорость как некоторую функцию от х:

Отсюда

И, следовательно,

Последнее уравнение устанавливает зависимость между х и , т.е. дает искомый закон движения точки. Остается выполнить интегрирование и затем решить полученное уравнение, если это возможно относительно х, т.е. выразить х как явную функцию переменной .