Вопрос 36. Скорость точки в криволинейном движении

Скорость точки в криволинейном движении представляет собой векторную величину, характеризующую для каждого данного момента быстроту движения точки и направление этого движения.

Пусть точка М описывает данную криволинейную траекторию, двигаясь по закону , где дуговая координата этой точки (рис.11.3)

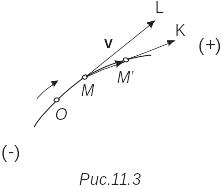
Пусть в момент времени t движущаяся точка занимает положение М на траектории. Пусть через малый промежуток времени Δt (в момент t+ Δt) та же точка занимает положение М'. Тогда или .

Вектор называется средней скоростью точки за время Δt. Обозначим скорость точки . При приближении Δt к нулю, в пределе направление вектора совпадает с направлением касательной к траектории в точке М, а модуль его будет равен .

Пусть вектор, представляющий предел при Δt→0, изображается вектором . Предел средней скорости при Δt→0 называется скоростью движущейся точки в момент времени t.

Если обозначим эту скорость через , то

Для модуля скорости имеем:

Предел отношения бесконечно малой дуги к стягивающей ее хорде равен 1. Поэтому , следовательно,

Если производная положительная, то с увеличением t величина s возрастает, следовательно, точка движется в положительном направлении по траектории; если эта производная отрицательная, то точка движется по траектории в отрицательном направлении. В последнем случае при определении модуля скорости производную надо брать по абсолютному значению.

Скорость направлена по касательной к траектории, и равна по модулю абсолютному значению производной от дуговой координаты движущейся точки по времени.

Рис.11.4.

Вопрос 37. Ускорение точки в криволинейном движении

В случае криволинейного движения производная скорости по времени не может полностью характеризовать изменение скорости со временем, так как скорость в этом случае изменяется не только по модулю, но и по направлению.

Ускорение точки в криволинейном движении выражается векторной производной от скорости по времени.

Т.о. ускорение точки в криволинейном движении есть вектор, который строится следующим образом: пусть в момент t движущаяся точка занимает на траектории положение М (рис.11.5) и имеет скорость v.

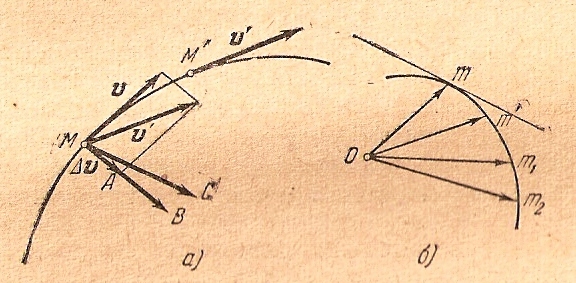Рис.11.5.

Пусть через малый промежуток времени Δt, т.е. в момент t+ Δt, эта точка займет положение М' и достигнет скорости v'. Перенесем начало вектора v' в точку М и соединим конец вектора v' с концом вектора v и дополним полученный треугольник до параллелограмма. Тогда вектор представит собой векторное изменение скорости за время Δt, так как .

Построим вектор , равный отношению изменения скорости к соответствующему промежутку времени Δt:

Этот вектор называется средним ускорением точки за время Δt.

Так как при делении вектора на положительную скалярную величину Δt его направление не изменяется, то направление среднего ускорения совпадает с направлением вектора .

Предел, к которому стремится среднее ускорение при Δt→0, называется ускорением точки в данный момент t. Мы будем обозначать ускорение через .

Следовательно, .

Пусть на рис.11.5 а вектор есть вектор, к которому стремится в пределе при среднее ускорение , тогда .

Если проведем из какой-нибудь неподвижной точки О векторы и т.д. (рис.11.5 б), равные скоростям v, v' и т.д. движущейся точки М в различные моменты времени, то геометрическое место концов этих векторов представляет собой годограф вектора v, или годограф скорости. Согласно определению векторной производной, ускорение точки М параллельно касательной к годографу скорости в соответствующей точке m.