Вопрос 34. Уравнение движения точки и график движения

Пусть точка М описывает прямолинейную траекторию (рис.10.1). Примем эту прямую за ось х и будем определять положение точки на траектории ее абсциссой ОМ=х. Причем точка О есть произвольно выбранная на траектории неподвижная точка (начало координат).

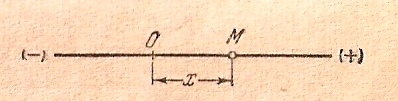Рис.10.1.

Так как при движении точки М каждому моменту времени (каждому числовому значению переменного t) соответствует единственное определенное положение этой точки на оси х и так как при перемещении точки М из одного положения в другое она последовательно проходит через все промежуточные положения, то абсцисса точки М является некоторой однозначной и непрерывной функцией времени, что в общем виде можно записать так: (1)

Это уравнение называется уравнением движения или законом движения точки М по оси х. В зависимости от вида функции f мы будем иметь различные виды движения точки по прямолинейной траектории. Если известен закон движения , то для каждого произвольно выбранного момента времени можно найти соответствующее значение х и, следовательно, можем рассчитать положение точки М на ее траектории в любой момент времени. Таким образом, уравнение движения полностью определяет движение точки по заданной прямолинейной траектории.

Для наглядного представления о характере движения точки применяют графический способ. Уравнение движения на чертеже изображается, как функциональная зависимость между двумя переменными, между х и t. График функции , называется графиком движения или кривой расстояний.

По оси абсцисс откладываются значения времени как независимого аргумента t. Эта ось называется осью времени. По оси ординат откладывают значения пройденного расстояния х. Эта ось называется осью расстояний.

Масштаб изображения единиц времени и единиц расстояния выбирается произвольно. Давая различные числовые значения t, из уравнения движения находятся значения х. Получив ряд значений t и х, можно построить по этим координатам график движения точки. На рис.10.2 показан график прямолинейного движения точки, уравнение которого имеет вид

Рис.10.2

Равномерное движение точки

Пусть точка находившаяся в начальный момент (t=0) в положении М₀, движется по оси х (рис.10.3.)

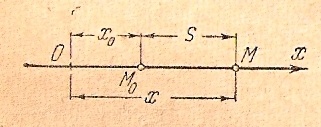Рис.10.3

Начальное расстояние ОМ₀ обозначим через х₀, переменную абсциссу ОМ обозначим через х. Тогда расстояние М₀М является длиной пути, пройденного точкой за t секунд. Обозначая длину пути через S, получим:

(2)

Равномерным движением точки называется такое движение, при котором отношение пройденного пути к соответствующему промежутку времени остается постоянным для любого промежутка времени.

Следовательно, при равномерном движении будем иметь:

Отношение пути ко времени называется скоростью равномерного движения и обозначается буквой v, т.е 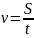(3)

Отсюда получаем, что (4), т.е. путь пройденный точкой при равномерном движении, равен произведению скорости на время.

Аналогично, (5) т.е., время, в течение которого точка при равномерном движении проходит данный путь, равно отношению этого пути к скорости.

Эти равенства являются основными формулами для равномерного движения. По этим формулам определяется одна из трех величин, когда две другие известны. Размерность скорости .

Подставляя в уравнение (4) значение пути (2), получим: (6)

Уравнение (6), выражающее зависимость между переменными х и t, представляет собой закон равномерного движения. Так как это уравнение первой степени относительно переменных х и t, то график равномерного движения – прямая линия (рис.10.3).

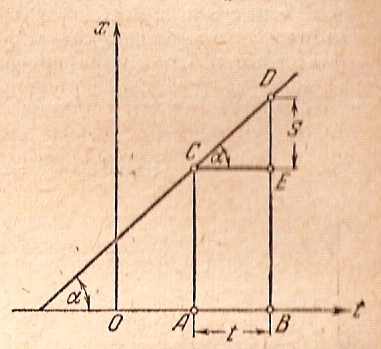Рис.10.3.

Чтобы определить скорость данного движения, нужно путь S разделить на время t: (7)

Скорость равномерного движения численно равна тангенсу угла между осью времени и прямолинейным графиком этого движения.

Этот результат верен только в случае, когда при построении графика движения масштаб для времени и расстояний взят одинаковый, т.е. если единица времени и единица расстояния на обеих осях изображаются отрезками одинаковой длины.

Пусть масштаб изображения пути равен m, отрезок изображающий путь σ, масштаб времени n, а отрезок изображающий время τ. Тогда , но , т.е.

Скорость точки при неравномерном движении

Пусть точка движется по оси х, по закону . Пусть произвольная нелинейная функция. График движения в этом случае будет изображаться некоторой кривой линией. Такое движение называют неравномерным.

При неравномерном движении отношение пройденного пути к соответствующему промежутку времени не является постоянной величиной, следовательно, расстояния проходимые точкой за одинаковые промежутки времени не равны между собой.

Если составить отношение пути S, пройденного точкой при неравномерном движении, ко времени t, в течение которого этот путь пройден, то это отношение дает нам среднюю скорость за данный промежуток времени t или на данном пути S. Среднюю скорость будем обозначать через v*, следовательно:

Средняя скорость характеризует быстроту движения за некоторый данный промежуток времени, но не дает представления о быстроте движения точки в отдельные моменты этого промежутка времени. Поэтому, кроме средней скорости, необходимо определять мгновенную скорость или скорость точки в данный момент. Пусть в данный момент t точка занимает на траектории положение М (рис.10.4).

Рис.10.4.

Через некоторый весьма малый промежуток времени Δt, т.е. в момент времени t+Δt, точка займет положение М'. Расстояние ОМ' обозначим через х', причем . Путь пройденный точкой за время Δt будет равен отрезку ММ', причем

Следовательно, средняя скорость за время Δt будет равна .

Предел, к которому стремится средняя скорость , когда промежуток времени Δt стремится к нулю, называется скоростью точки в данный момент t:

Скорость точки в прямолинейном движении равна производной от абсциссы движущейся точки по времени.

Если производная положительна, то х с течением времени возрастает и движение происходит в положительном направлении оси х. Если производная при данном значении t отрицательно, то х с течением времени убывает и точка движется по оси х в отрицательном направлении.

Таким образом, определение скорости при неравномерном движении, закон которого известен, сводится к дифференцированию известной функции .

Ту же задачу можно решить и графическим путем. Пусть нам дан график движения, изображаемый некоторой кривой линией, уравнение которой есть (рис.10.5)

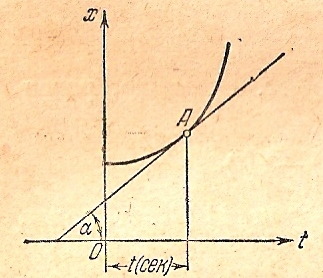Рис.10.5

Найдем скорость движущейся точки в некоторый момент времени t. Возьмем на данной кривой точку А, абсцисса которой имеет заданную величину t, и проведем через эту точку касательную к этой кривой. Угол касательной с осью времени обозначим через α. Так как производная от функции равна тангенсу угла наклона касательной с осью абсцисс, то .

Скорость точки при неравномерном движении численно равна тангенсу угла, между касательной к графику движения и осью времени.

Этот результат верен лишь в том случае, когда на графике движения величины х и t изображаются в одинаковом масштабе. При разных масштабах будем иметь ту же формулу, что и в случае равномерного движения

Скорость точки при неравномерном движении, определяемая по формуле представляет собой переменную величину, являющуюся функцией времени. Если изобразить функциональную зависимость между v и t графически, в виде соответствующей кривой, то эта кривая называется графиком скорости или кривой скоростей. Для построения графика скорости в прямоугольных координатах по оси абсцисс откладывают значения времени t, а на оси ординат - значения скорости v. Задавая переменному времени t в уравнении числовые значения и вычисляя соответствующие значения скорости v, строится график скорости. График скорости равномерного движения изображается прямой линией, параллельной оси времени.