Вопрос 3. Аксиомы статики

Совокупность сил, приложенных к данному твердому телу, называется системой сил.

Если под действием данной системы сил твердое тело остается в покое (по отношению к выбранной инерциальной системе отсчета) или движется поступательно, равномерно и прямолинейно, т.е. так, что все его точки движутся по прямым линиям с одинаковой постоянной скоростью, то такое состояние тела называется состоянием равновесия, а приложенная к нему система сил называется уравновешивающей системой. Одна из сил уравновешивающей системы называется уравновешивающей по отношению ко всем остальным.

Если одну систему сил, приложенных к твердому телу, можно заменить другой системой, не нарушая при этом его покоя или не изменяя его движения, то такие системы сил называются эквивалентными. Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил.

В основе статики лежат некоторые элементарные положения, которые называются аксиомами.

Аксиома 1 Для равновесия двух сил, приложенных к абсолютно твердому телу, необходимо и достаточно, чтобы эти силы были равны по модулю и направлены по прямой, соединяющей их точки приложения, в противоположные стороны.

Аксиома 2 Не изменяя действия данной системы сил на абсолютно твердое тело, можно прибавить к этой системе или отнять у нее две уравновешивающие силы, т.е. две силы равные по модулю и направленные по одной прямой в противоположные стороны.

Следствие 1 Не изменяя действия одной силы на тело, точку приложения этой силы можно переносить по ее линии действия (рис.1.1)

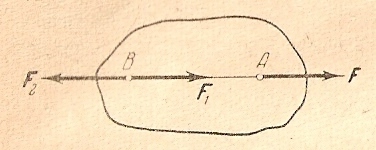Рис.1.1.

Следствие 2 Если к телу приложена уравновешивающая система сил, то одна из этих сил, взятая в обратном направлении является равнодействующей всех сил.

Аксиома 3 Равнодействующая двух сил, приложенных к абсолютно твердому телу в одной точке, равна их геометрической сумме, т.е. выражается по модулю и направлению диагональю параллелограмма, построенного на этих силах (рис.1.2)

Если обозначим через R равнодействующую двух данных сил F₁ и F₂, на основании этой аксиомы имеем: 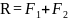Знак + здесь обозначает операцию геометрического сложения.

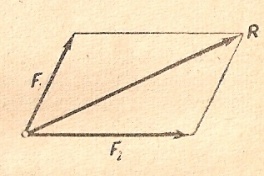Рис.1.2.

Теорема. Если три непараллельные силы, лежащие в одной плоскости, уравновешиваются, то их линии действия пересекаются в одной точке.

Доказательство. Пусть данное тело находится в равновесии под действием трех сил F₁, F₂ и F₃,приложенных в точках А₁, А₂ и А₃ (рис.1.3) Продолжим линии действия сил F₁ и F₂ до их пересечения в точке В; перенесем их точки приложения в точку В и сложим эти силы по правилу параллелограмма; получим равнодействующую силу R.

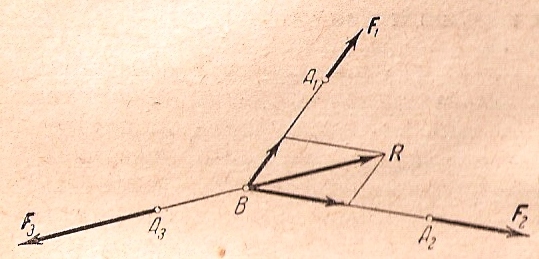Рис.1.3.

Если заменить силы F₁ и F₂ одной эквивалентной им силой R, то равновесие не нарушится; следовательно, силы R и F₃ также уравновешиваются, а потому эти две силы должны быть равны по модулю, и направлены по одной общей прямой в противоположные стороны (аксиома 1). Поэтому линия действия силы F₃ совпадает с линией действия силы R и, следовательно, проходит через точку В, что и требовалось доказать.

Аксиома 4 Силы, с которыми действуют друг на друга два тела, всегда равны по модулю и направлены по одной прямой в противоположные стороны.

Этот закон был сформулирован впервые Ньютоном в его «Началах» и называется законом равенства действия и противодействия. Важно заметить, что действие и противодействие представляют собой две силы, приложенные к двум разным телам. Поэтому нельзя сказать, что эти две силы уравновешиваются в том смысле, как это говорят о двух численно равных силах, приложенных к одному и тому же твердому телу и направленных по одной прямой в противоположные стороны.

Аксиома 5 Если деформируемое (не абсолютно твердое) тело, находящееся под действием данных сил в состоянии равновесия, станет абсолютно твердым (отвердеет), то его равновесие не нарушится.

Этот закон называется принципом отвердевания; он имеет значение при изучении равновесия деформируемых тел. Из этого закона следует, что условия, которым должны удовлетворять при равновесии силы, приложенные к абсолютно твердому телу, необходимо должны соблюдаться и при равновесии деформируемого тела.