
- •Вопрос 1. Абсолютно твердое тело. Материальная точка. Система отсчета.
- •Вопрос 2. Понятие силы
- •Вопрос 3. Аксиомы статики
- •Вопрос 4. Связи и реакции связей
- •Вопрос 5.Сложение сил, приложенных в одной точке
- •Вопрос 6.Разложение силы
- •Вопрос 7.Проекция вектора на ось
- •Вопрос 8.Умножение вектора на скаляр. Единичный вектор
- •Вопрос 9. Разложение вектора по координатным осям
- •Вопрос 10.Аналитический способ сложения сил
- •11.Равновесие системы сходящихся сил
- •Вопрос 12.Момент силы относительно точки. Условие равновесия рычага
- •Вопрос 14. Момент пары
- •Вопрос 15. Эквивалентные пары. Момент пары как вектор
- •Вопрос 16.Момент силы относительно точки
- •Вопрос 17.Приведение плоской системы сил к данному центру
- •18.Равнодействующая плоской системы сил. Теорема Вариньона
- •Вопрос 19. Приведения плоской системы сил к одной паре
- •Вопрос 20. . Условия равновесия плоской системы сил
- •Вопрос 21. . Равновесие системы, состоящей из нескольких твердых тел
- •Вопрос 22. Трение скольжения
- •Вопрос 23. Трение качения
- •Вопрос 24. Момент силы относительно оси
- •Вопрос 25. Формулы для моментов силы относительно координатных осей
- •26.Момент силы относительно точки как вектор
- •Вопрос 29. Равнодействующая системы сил. Теорема Вариньона
- •Вопрос 30. Условия равновесия системы сил в общем случае
- •Вопрос 31. Равновесие несвободного тела
- •Вопрос 32. Общие формулы для координат центра тяжести
- •Вопрос 33. Положение центра тяжести симметричного тела
- •Вопрос 34. Уравнение движения точки и график движения
- •Вопрос 35. Определение пути, пройденного точкой, по заданному закону изменения ее скорости
- •Вопрос 36. Скорость точки в криволинейном движении
- •Вопрос 37. Ускорение точки в криволинейном движении
- •Вопрос 38. Определение скорости и ускорения из уравнений движения точки в декартовых координатах
- •Вопрос 39. Проекция ускорения на естественные оси. Касательное и нормальное ускорения
- •Вопрос 40. Поступательное движение твердого тела
- •Вопрос 41. Вращение твердого тела вокруг неподвижной оси
- •Вопрос 42. Угловая скорость как вектор. Выражение линейной скорости и касательного и нормального ускорений в виде векторных произведений
- •Вопрос 43.Сложное движение точки. Относительное, переносное и абсолютные движения
- •Вопрос 44. Относительные, переносные и абсолютные скорость и ускорение точки
- •Вопрос 45. Уравнения плоскопараллельного движения твердого тела
- •Вопрос 46.Разложение движения плоской фигуры на поступательное и вращательное
- •Вопрос 47. Уравнения движения свободного тела в общем случае. Разложение движения твердого тела на поступательное движение и движение вокруг некоторой точки.
- •Вопрос 48. Основные законы динамики.
- •Вопрос 49 . Дифференциальные уравнения движения материальной точки
- •18.3. Две основные задачи динамики точки
- •Вопрос 50. Дифференциальное уравнение прямолинейного движения точки
- •Вопрос 51. Прямолинейное Движение точки под действием силы.
- •Вопрос 52.Теорема о количестве движения
- •Вопрос 53. Теорема о моменте количества движения
- •Вопрос 54. Работа
- •Вопрос 55. Теорема о кинетической энергии материальной точки
- •Вопрос 57. Понятие о потенциальной энергии
- •Вопрос 58. Закон сохранения механической энергии
- •Вопрос 59. Принцип Даламбера для материальной точки.
- •Вопрос 60. Цели и задачи сопротивления материалов
- •Вопрос 61. Внешние и внутренние силы
- •Вопрос 62. Нормальные и касательные напряжения
- •Вопрос 63. Линейное (одноосное) напряженное состояние
- •Вопрос 64. Плоское (двухосное) напряженное состояние
- •Вопрос 65. Главные напряжения
- •Вопрос 68 Круги Мора для трехосного напряженного состояния
- •Вопрос 70. Относительное удлинение и угол сдвига
- •Вопрос 71. Компоненты тензора деформации
- •Вопрос72. Относительное объемное расширение
- •Вопрос 73. Условия совместности деформаций
- •Вопрос 78. Поперечное сжатие. Коэффициент Пуассона.
- •Вопрос 79 и 80. Предел текучести, течение материала, упрочнение, разрыв.
- •Вопрос 81. Предел упругости
- •Вопрос 82. Сжатие стального образца
- •Вопрос 83. Растяжение сжатие других технически важных материалов
- •Вопрос 84. Твердость
- •Вопрос 85. Переменная нагрузка
- •Вопрос 88. Закон Гука в общей форме
- •Вопрос 89. Теории прочности
- •Вопрос 90. Закон Гука для сдвига. Модуль сдвига
Вопрос 24. Момент силы относительно оси
Пусть
дана сила F,
изображаемая вектором
 ,
и какая-нибудь ось z (рис.7.1) Проведем
через точку приложения А этой силы
плоскость, перпендикулярную к оси z.
Точку пересечения этой плоскости с
осью z обозначим ее через О. Разложим
силу F
на две составляющие: параллельную оси
z и другую f
перпендикулярную этой оси, и опустим
из точки О перпендикуляр на линию
действия силы f, длину которого обозначим
h.
,
и какая-нибудь ось z (рис.7.1) Проведем
через точку приложения А этой силы
плоскость, перпендикулярную к оси z.
Точку пересечения этой плоскости с
осью z обозначим ее через О. Разложим
силу F
на две составляющие: параллельную оси
z и другую f
перпендикулярную этой оси, и опустим
из точки О перпендикуляр на линию
действия силы f, длину которого обозначим
h.
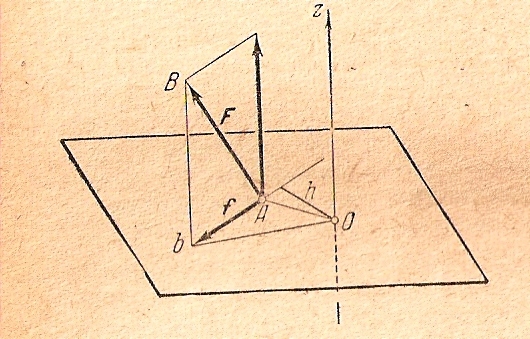 Рис.7.1.
Рис.7.1.
Пусть сила F приложена к твердому телу, которое может вращаться вокруг неподвижной оси z, например к двери вращающейся на петлях вокруг оси z (рис.7.2), то очевидно, что составляющая силы F, параллельная этой оси, не может сообщить телу вращательного движения. Эта составляющая стремится только сдвинуть тело вдоль оси z. Вращательный эффект вызывает составляющая сила f.
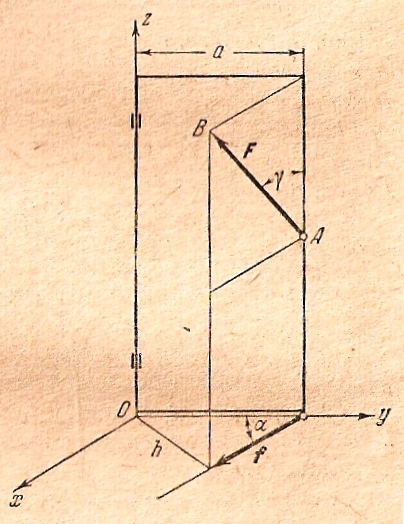 Рис.7.2.
Рис.7.2.
Но при рассмотрении задачи о равновесии рычага, показано, что мерой вращательного эффекта силы, лежащей в плоскости, перпендикулярной к оси вращения тела, является ее момент относительно точки пересечения оси вращения с этой плоскостью. Следовательно, мерой вращательного эффекта силы F, приложенной к телу, вращающемуся вокруг оси z, является момент относительно точки О составляющей f, перпендикулярной к оси z. Поэтому момент силы f относительно точки О, т.е. взятое с соответствующим знаком произведение fh, называется моментом силы F относительно оси z.
Моментом силы относительно оси называется момент проекции этой силы на плоскость, перпендикулярную к данной оси, относительно точки пересечения этой оси с этой плоскостью,
Или взятое со знаком плюс или минус произведение модуля проекции силы на плоскость, перпендикулярную к данной оси, на расстояние этой проекции от точки пересечения данной оси с этой плоскостью:
 или
или

Этот момент считается положительным, если для наблюдателя, смотрящего с положительного конца оси z на перпендикулярную к ней плоскость, в которой лежит сила f, эта сила стремится повернуть тело в направлении, обратном движению часовой стрелки. В противном случае момент силы F относительно оси z считается отрицательным.
Из данного определения момента силы относительно оси следует:
Момент силы относительно оси равен нулю в том случае, когда линия действия силы пересекает ось при плече h равном нулю или когда сила параллельна этой оси при этом составляющая f=0
Момент силы относительно данной оси не изменяется при переносе точки приложения силы в другую точку по линии ее действия, так как при таком переносе точки приложения силы не изменяются ни проекция f, ни длина плеча (перпендикуляра h)
Вопрос 25. Формулы для моментов силы относительно координатных осей
Пусть дана сила F, приложенная к телу в точке А, координаты которой обозначим х, у и z. Проекции этой силы на координатные оси обозначим через Х, Y и Z (рис.7.3)
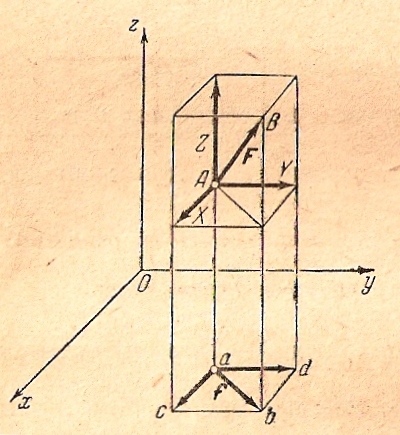 Рис.7.3.
Рис.7.3.
Найдем
момент силы F
относительно оси z. Для этого спроектируем
силу эту силу на плоскость Оху и обозначим
ее проекцию через f.
Тогда

Разложим
вектор f
на две составляющие
 ,
параллельные осям х и у. Эти составляющие
равны по модулю проекциям силы F
на оси х и у, т.е ac=X
и ad=Y.
,
параллельные осям х и у. Эти составляющие
равны по модулю проекциям силы F
на оси х и у, т.е ac=X
и ad=Y.
На основании теоремы Вариньона получим:
 ,
следовательно
,
следовательно
 .
.
Но,
так как (рис.7.4)
 и
и

То
 .
.
Аналогично
можно получить остальные формулы:
 ;
;

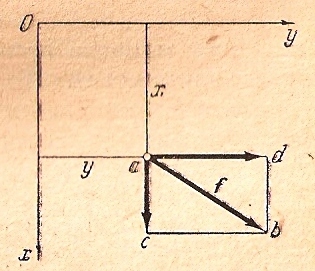 Рис.7.4.
Рис.7.4.
