
- •1.Частн.Прирощ., произв., диф., их геом.Смысл.
- •2. Полный диф.Ф-ции нескольких переменных. Инвариантность ф-ции полн.Диф.
- •3. Необход. И дост. Условие диф. Ф-ции
- •6. Экстремум ф-ции нескол. Переем. Необх. И дост. Усл.
- •8. Первообр. Ф-ции и неопред. Инт.
- •12. Инт. Рациональных дробей
- •14. Инт. Тригонометрических выражений
- •15. Инт. Некот иррациональных выражений
- •16. Определенный инт. Геометр.Смысл
- •4. Произв.Сложных и неявнозад.Ф-ций
- •5. Кас.Пл. И норм. К поверхн. Скал.Поле. Градиент
- •7. Условный экстр. Метод множит. Лагранжа
- •11. Замена переменной в неопред. Инт.
- •13. Инт. Простейших рациональных ф-ций
- •17. Основные св-ва опред. Инт.
- •18. Формула Ньютана-Лейбница
- •19. Опред.Инт. С переменным верхним пределом
4. Произв.Сложных и неявнозад.Ф-ций
Е![]() сли
уравнение
сли
уравнение
 задает
задает
 как неявную ф-ию аргумента
как неявную ф-ию аргумента
 ,
т. е.
,
т. е.
 ,
то при нахождении произв. этой ф-ции
предполагают, что в данное ур-ие вместо
подставлено соответствующее выражение
,
то при нахождении произв. этой ф-ции
предполагают, что в данное ур-ие вместо
подставлено соответствующее выражение
 и получено тождество
и получено тождество
 .
Затем диф. по
это тождество (не забывая, что
есть ф-ция аргумента
)
и решают полученное ур-ние относительно
искомой произв.
.
Затем диф. по
это тождество (не забывая, что
есть ф-ция аргумента
)
и решают полученное ур-ние относительно
искомой произв.


5. Кас.Пл. И норм. К поверхн. Скал.Поле. Градиент
Кас.
Пл. Т к поверхности С в данной т.М наз.
пл., кот содержит все кас. к кривым,
проведенным на поверхности через эту
т. Ур-ние касс.
 Прямая перпенд. к кас. Пл. в точке касания
наз. норм.к поверхности в этой т.
Прямая перпенд. к кас. Пл. в точке касания
наз. норм.к поверхности в этой т. .
Пусть в каждой т.М некот.обл. D
задано значение скалярной физ. величины
U,т.е.
такой вел., кот полностью х-ризуется
своим числ.знач. Например, это может
быть температура точек неравномерно
нагреваемого тела. Это и наз. скалярной
величиной точки. Если в обл.D
задана скал. ф-ция точки U(M),
то гов., что в этой обл. задано скал.
поле.Важной
х-кой скал.поля явл. скорость изменения
поля в заданном направлении. Произв.
ф-ции U=U(x,y,z)
в т.M(x,y,z)
по направлению
.
Пусть в каждой т.М некот.обл. D
задано значение скалярной физ. величины
U,т.е.
такой вел., кот полностью х-ризуется
своим числ.знач. Например, это может
быть температура точек неравномерно
нагреваемого тела. Это и наз. скалярной
величиной точки. Если в обл.D
задана скал. ф-ция точки U(M),
то гов., что в этой обл. задано скал.
поле.Важной
х-кой скал.поля явл. скорость изменения
поля в заданном направлении. Произв.
ф-ции U=U(x,y,z)
в т.M(x,y,z)
по направлению
 наз.
наз.
 .
Градиентом ф-ции U=U(x,y,z)
в т.M(x,y,z)
наз. вектор, корд. кот равны соотв.
частным произв. этой ф-ции в т М:
.
Градиентом ф-ции U=U(x,y,z)
в т.M(x,y,z)
наз. вектор, корд. кот равны соотв.
частным произв. этой ф-ции в т М:
 .
Произв. по направл.
.
Произв. по направл.
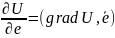 .
Направление градиента есть направление
наибыстрейшего возрастания скалярного
поля в данной т, а модуль градиента =
наибольшей скорости возрастания
скал.поля в данной т.
.
Направление градиента есть направление
наибыстрейшего возрастания скалярного
поля в данной т, а модуль градиента =
наибольшей скорости возрастания
скал.поля в данной т.
7. Условный экстр. Метод множит. Лагранжа
Усл.
экстр. ф-ции f(x,y)
наз max
или min
этой ф-ции, достигнутый при условии,
что ее оргументы удовлетворяют ур-нию
связи
 .
Чтобы найти усл.экстр. методом множителей
Лагранжа нужно: 1) Сост. ф-цию Лагранжа
.
Чтобы найти усл.экстр. методом множителей
Лагранжа нужно: 1) Сост. ф-цию Лагранжа
 ,
где
,
где
 - множитель Лагр.; 2) вычислить частные
произв. ф-ции Лагр. по
- множитель Лагр.; 2) вычислить частные
произв. ф-ции Лагр. по
 ;
3) сост. с-му ур-ний
;
3) сост. с-му ур-ний
 4) измен. знак
2-го диф. ф-ции Лагр.
4) измен. знак
2-го диф. ф-ции Лагр.
 для всех
значений
найденных из с-мы при условии
для всех
значений
найденных из с-мы при условии
 Тогда ф-ция
f(x,y
имеет усл.
Мах, если
Тогда ф-ция
f(x,y
имеет усл.
Мах, если
 и усл. Мin,
если
и усл. Мin,
если
 .
В частности,
если в стац. Т
.
В частности,
если в стац. Т
 ,
а А<0, то имеем усл мах, если
,
a
A>0
(C>0)
– min.
,
а А<0, то имеем усл мах, если
,
a
A>0
(C>0)
– min.
9. Осн. св-ва неопред. инт.
1.
Произв. от неопред. инт. = подынтегр.
ф-ции, диф. от неопред. инт. =
подынтегр.выражению:
![]() 2. Неопред. инт. от диф. некот. ф-ции =
сумме этой ф-ции и произвольной
постоянной:
2. Неопред. инт. от диф. некот. ф-ции =
сумме этой ф-ции и произвольной
постоянной:
![]() 3. Постоянный множитель a(a≠0) можно
выносить за знак неопред. инт.:
3. Постоянный множитель a(a≠0) можно
выносить за знак неопред. инт.:
![]() 4. Неопред. инт. от алгебр. суммы конечного
числа = алгебр. сумме инт. от этих ф-ций:
4. Неопред. инт. от алгебр. суммы конечного
числа = алгебр. сумме инт. от этих ф-ций:
5.
Если F(x) – первообр.ф-ции f(x), то
![]() 6. Инвариантность ф-л инт.: любая
ф-ла инт.сохраняет свой вид, если
переменную инт. заменить любой диф.
ф-цией этой перем.
6. Инвариантность ф-л инт.: любая
ф-ла инт.сохраняет свой вид, если
переменную инт. заменить любой диф.
ф-цией этой перем.
![]() .
.
11. Замена переменной в неопред. Инт.
в
инт. переменную x заменяют переменной
t по ф-ле
 откуда dx =ϕ′(t)dt. Пусть ф-ция x = ϕ(t)
определена и диф. на некот множестве
Т и пусть Х – множество знач. этой ф-ции,
на кот определена ф-ция f(x). Тогда если
на множестве Х функция f(x) имеет
первообр., то на множестве Т справед.
ф-ла ∫f
(x)dx=∫f(ϕ (t ))ϕ′ (t)dt
откуда dx =ϕ′(t)dt. Пусть ф-ция x = ϕ(t)
определена и диф. на некот множестве
Т и пусть Х – множество знач. этой ф-ции,
на кот определена ф-ция f(x). Тогда если
на множестве Х функция f(x) имеет
первообр., то на множестве Т справед.
ф-ла ∫f
(x)dx=∫f(ϕ (t ))ϕ′ (t)dt
Метод «подведения» подынтегр. ф-ции под знак
диф. По опред. диф. ф-ции ϕ′(x)dx =d(ϕ(x))
