5. Асимптоты графика функции.

Определение 1. Асимптотой графика функции y=f(x) называется прямая, расстояние до которой от точки (x, f(x)) стремится к нулю при неограниченному удалении точки от начала координат.

Н а графиках изображены вертикальная, горизонтальная и наклонная асимптоты.

Теорема 1. Если функция y=f(x) определена в некоторой окрестности точки х0, и хотя бы один из пределов функции при х→ х0-0 (слева) или при х→ х0+0 (справа) равен бесконечности (т.е. lim f(x) = ∞ при х→ х0-0 и lim f(x) = ∞ при х→ х0+0), тогда прямая х=х0 является вертикальной асимптотой графика y=f(x).

Теорема 2. Если функция y=f(x) определена при достаточно больших х и существует конечный предел функции lim f(x) = b при х→ ∞, тогда прямая y=b является горизонтальной асимптотой графика y=f(x).Теорема 3. Если функция y=f(x) определена при достаточно больших х и существуют конечные пределы функции lim f(x)/х = k при х→ ∞, и lim [f(x)-kх] = b при х→ ∞, тогда прямая y=kx+b является наклонной асимптотой графика y=f(x).

6. Нахождение наибольшего и наименьшего значения функции.

1) нахожд. крит. . 1-го рода. 2) вычислить знач f-и в КТ и на концах отрезка. 3) среди знач выбрать наи-> и наи-< знач.

Теорема (для произвольн. пром.): пусть y=f(x) непрерывна на произв. промежутке (a,b) и имеет на этом пром. лиш 1 экстремум: 1) если max –наибольш. знач. 2) наоборот.

6. Нахождение наибольшего и наименьшего значения функции.

1) нахожд. крит. . 1-го рода. 2) вычислить знач f-и в КТ и на концах отрезка. 3) среди знач выбрать наи-> и наи-< знач.

Теорема (для произвольн. пром.): пусть y=f(x) непрерывна на произв. промежутке (a,b) и имеет на этом пром. лиш 1 экстремум: 1) если max –наибольш. знач. 2) наоборот.

7. Понятие функции нескольких переменных. Определение предела и непрерывности функции двух переменных.

опр: если кажд паре действ чисел (x, y) ∈D соотв. 1 опр. число z, то говор что на множест D задана f-я z=f(x,y) со знач воо мн z. предел: число А наз пред f-и f(x,y)в . (x_о,y_о) если для любой послед .-к ((x_n,y_n) 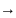(x_о,y_о), координ кот отличны от (x_о,y_о) и не вых из обл опр f-и . непрерывн: f-я назыв непрер в . (x_о,y_о) если в этой . сущ lim и он = знач f-и в этой точке.

8. Частные производные и полный дифференциал функции нескольких переменных.

Опр: если сущ lim отнош при то этот lim назыв частной производной по х f-и f(x,y) в . (x,y) и обазнач f’_x(x,y). Полный диф. f(x,y) назыв . Полный диф – сумма частных диф.

9. Экстремум функции нескольких переменных. Необходимые условия.

опр. . с координ назыв . экстрем если сущ такая -окресность этой . что для всех . с координ (х,у) взятых из окресности кроме выполн равенство.1) . теорема: если точка с координ явл . экстрем f z=f(x,y) и в этолй точке сущ обе части произв то эти произв в . = 0

16. Интегрирование выражений, содержащих тригонометрические функции. Вычисление неопределнных интегралов типа R(sinx,cosx)dx сводится к вычислению интегралов от рациональной функции подстановкой tg , которая называется универсальной.sinx= = , cosx = = , x=2arctgt, dx= Поэтому R(sinx;cosx)dx = R( ) =R₁(t)dt , где R₁(t) – рациональная функция от t.

Интегралы вида sinⁿxcos^mxdx ( m,n ;m≥0,n≥0 ).Для нахождения таких интегралов используются следующие приемы: 1.подстановка sinx=t если n-целое положительное нечетное число 2.Подстановка cosx=t если m- целое положительное нечетное число 3. Формулы понижения порядка:cos²x= (1+cos2x), sin²x= (1-cos2x),sinxcosx= sin2x ,если m и n - целые неотрицательные четные числа 4. Подстановка tgx=t, если m+n – есть четное отрицательное целое число.

Интегралы вида , (n ). Для нахождения этих интегралов примен. ф-лы, с пом. кот. помлед-но понижается степень m. tg2x = (1/cos2x) - 1, ctg2x = (1/sin2x) – 1 1/cosx = secx, 1/sinx = cosecxtg2x = sec2x - 1, ctg2x = cosec2x – 1 Замечание. Если m-степень частная, то удобно делать подст. tg x = t., тогда x = arctg t. dx = dt/ (1+t2) и интеграл сводится к интегралу от непр. рацион. дроби.

17. Геометрическая задача, приводящая к понятию определенного интеграла. Определение определенного интеграла. Сумма вида называется интегральной суммой функции y=f(x) на отрезке [a;b]. Если интегральная сумма Sn имеет предел I,который не зависит ни от способа разбиения отрезка [a;b] на частичные отрезки , ни от выбора точек в них, то число I называется определенным интегралом от функции y = f(x) на отрезке [a;b] и обозначается . Таким образом, = Геом.смысл: Определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

18. Свойства определенного интеграла 1 . 2. Для любого действительного числа с : 3. 4.

5. 6.Аддитивность: если есть a<c<b, то 7.f(x)≥0 → ≥08. Монотонность: f(x)≥g(x) 9. Об оценке определенного интегралы:m Пусть на интервале [a,b], ф-ция f(x) принимает свое наименьшее m и наибольшее M значение. m(b-a)≤ ≤M(b-a)10. Теорема о среднем: при f(x)≥0 имеет простой геометрический смысл: значение определенного интеграла равно, при некотором площади cϵ(a,b) прямоугольника с высотой f(c) и основанием.b-a. Число f(c)= называется средним значением функции f(x) на отрезке [a;b].