23. Понятие двумерной дискретной св и таблица её распред-ия.

Опр. Двумерная С.В. (X; Y) наз. дискретной, если С.В. X и Y дискретны, т.е. конечны.

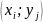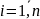Если С.В. Х может принимать только значения x₁,x₂…x_n , а С.В.Y – значения y₁, y₂…y_n , то двумерный случайныя вектор (X; Y)   может принимать только пары значений  , где , j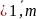 . Также, как и в одномерном случае, распред-ие двумерной дискретной С.В. естественно описывается с помощью таблицы:

24. Функция распред-ия двумерной с.В.

Опр. Двумерная С.В. (X; Y) наз. дискретной, если С.В. X и Y дискретны, т.е. конечны.

Опр. Функцией распред-ия F(x, y) двумерной С.В. (X,Y) наз. вер-ть того, что X < x , а Y < y. F(x ,y) = p(X < x, Y < y)

Замечание. Определение ф-ии распред-ия справедливо как для непрерывной, так и для дискретной С.В.

Св-ва: 1) 0 < F(x, y) < 1, т.к. F(x, y) явл. вер-тью;

2) F(x, y) есть неубывающая ф-ия по каждому аргументу.

F(x₂, y) F(x₁, y), если x₂ > x₁; F(x, y­₂) F(x, y₁), если y₂ > y₁;

3) Имеет место предельное соотношение:

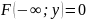
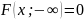
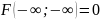
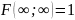
4) При y = ф-ия распред-ия двумерной С.В. становится ф-ий распред-ия составляющей X:

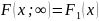
При x = ф-ия распред-ия двумерной С.В. становится ф-ий распред-ия составляющей Y:

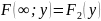
41.Понятие интерв-ной оценки параметров распред-ия. Доверит. Интервал для неизвест. Вер-ти для умеренно больших выборок.

Опр. Доверит. интервал по данным одной выборки и ориентированный на покрывании им истинного значения параметра с заданной надежностью наз. доверит. интервалом.

Опр. Оценка параметра распред-ия на основе доверит. интервала наз. интервальной оценкой параметра.

Оценка по умеренно большим выборкам (npq 10). Речь идет об оценке вер-ти события по её частоте для некот. Выборки объема n. Значения элементов выборки n = 0, если некот. событие не наступило в данном испытании, n = 1, если событие наступило. В кач-ве параметра выступает вер-ть наступления события в отд. испытании.

Выборка, полученная на основе наблюдения за n испытаниями подчинена биномиальному закону распред-ия. При биномиальный закон распред-ия стремится к норм. закону распред-ия с 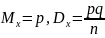, тогда С.В. распределена по закону Гаусса.

При заданной надежности опред-ся критич. Значение распред-ия Гаусса, для кот. выполняется:

; ; ;

; ;

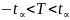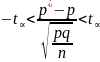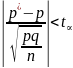
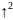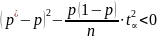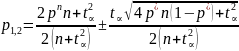
13. Математич. Ожидание случайных величин. Основные свойства.

Мат. ожиданием дискретной С.В. наз-ся величина, равная сумме произведений возможных значений случайных величин на соответствующие им вероятности.

Мат. ожидание характеризует средневзвешенную оценку возможного значения случайной величины.

Свойства: 1) М(С) = С, С=const; 2) M(kX)=k*M(X), k=const;

Док-во:

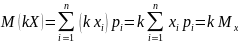
3) M(x+y)=M(x)+M(y); 4) M(x+c)=C+M(x); 5) M(x y)=M(x) M(y) , если X и Y – независим. С.В.