
- •9. Формула Бернулли и Пуассона.
- •10. Локальная и интегральная теоремы Муавра-Лапласа.
- •11. Способы задания закона распред-ния дискретных св. Их св-ва.
- •12. Способы задания закона распред-ния непрерывных св. Св-ва.
- •29. Закон больших чисел. Неравенство Маркова.
- •30. Закон больших чисел. Неравенство Чебышева.
- •31. Закон больших чисел. Теорема Чебышева.
- •32. Закон больших чисел. Теорема Бернулли.
- •43. Стат. Гипотеза. Общая схема её проверки. Ошибки 1 и 2 рода.
- •17. Тип.Зр непр.Случ.Величин. Равномерный закон распределения.
- •18. Тип.Зр непр. С.В. Показательный закон распред-ия.
- •19. Тип. Зр непр. С.В. Нормальный закон распределения.
- •20. Точные законы распред. С.В. Распред-е Пирсона (хи-квадрат).
- •37. Общие сведения о выборочном методе.
- •38. Точечная оценка параметров распред-ия. Требования к ф-иям выборки.
- •39. Понятие интервальной оценки параметров распред. Доверит. Интервал для неизвестного мат. Ожидания.
- •5. Совместные и несовместные события. Теорема слож-ия вер-тей.
- •7.Полная группа событий. Формула полной вероятности.
- •6. Зависимые и независ. События. Теорема умножения вер-тей.
- •8.Формула Байеса переоценки вер-тей гипотез. Её практич. Значение.
- •25. Плотность вер-ти двумерной с.В.
- •26. Условные законы распределения двумерной с.В.
- •27.Числовые характер-ки двумерной с.В.
- •28. Ковариация и коэффициент корреляции.
- •2. Относительная частота события (очс). Теорема Бернули.
- •3.Классич. Опред-ие вер-ти события. Формулы комбинаторики.
- •4. Геометрическое определение вероятности события.
- •23. Понятие двумерной дискретной св и таблица её распред-ия.
- •24. Функция распред-ия двумерной с.В.
- •41.Понятие интерв-ной оценки параметров распред-ия. Доверит. Интервал для неизвест. Вер-ти для умеренно больших выборок.
- •13. Математич. Ожидание случайных величин. Основные свойства.
- •14. Дисперсия случайных величин. Основные свойства.
- •15. Тип. Законы распред-ия дискрет. C.В. Бином. Закон распред-ия.
- •16. Тип. Законы распред-ия дискретных с.В. Распред-ие Пуассона.
- •34. Интегральная предельная теорема. Теорема Ляпунова.
- •35. Предмет мат. Статистики. Осн. Функция мат. Статистики.
- •36. Основные понятия математической статистики.
- •42. Понятие интерв-ной оценки параметров распред-ия. Доверит. Интервал для неизвест. Вер-ти для малых выборок.
- •45. Проверка гипотезы о равенстве средних двух совокупностей при известных дисперсиях.
- •44. Проверка гипотезы о равенстве средних двух совокупностей при неизвестных дисперсиях.
- •46. Проверка гипотезы о равенстве дисперсий двух совокупностей.
- •45. Проверка гипотезы о равенстве средних двух совокупностей при известных дисперсиях.
- •44. Проверка гипотезы о равенстве средних двух совокупностей при неизвестных дисперсиях.
- •46. Проверка гипотезы о равенстве дисперсий двух совокупностей.
- •47. Гистограмма распред-ия.
- •48. Проверка гипотезы о соответствии эмпирич. Закона распред-ия теоретич.
- •39. Понятие интерв-ной оценки параметров распред-ия. Доверит. Интервал для неизвест. Мат. Ожидания.
- •40. Понятие интерв-ной оценки параметров распред-ия. Доверит. Интервал для дисперсии.
2. Относительная частота события (очс). Теорема Бернули.
ОЧС- это отношение числа экспериментов, в кот. событие сост-лось к общему числу проведенных экспериментов.
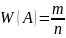 ,
где W(А)-
ОЧС, m
- число
экспер-тов,в кот событие А состоялось,
n
- это общее
число экспертов.
,
где W(А)-
ОЧС, m
- число
экспер-тов,в кот событие А состоялось,
n
- это общее
число экспертов.
Под стат. определением
вер-ти события А
понимают его относит-ную частоту, т.е. ,
где
Р*(А) - представляет
собой оценку (приближенное значение)
вер-ти события А.
,
где
Р*(А) - представляет
собой оценку (приближенное значение)
вер-ти события А.
Теорема Бернулли: Относит-ная частота события сходится по вер-ти к истинному значению вер-ти события с ростом числа экспертов.

Стат опред-ние вер-ти применимо при выполнении 3-х условий:
1.Должны сущ-вать возм-ности многократного воспроизв-ния экспер-тов на предмет наступления события А.
2.События должны обладать так называемой стат. устойчивостью осн. закономерностей.
3.Число проводимых экспериментов должно быть невелико.
3.Классич. Опред-ие вер-ти события. Формулы комбинаторики.
Исходы эксперимента наз-ся равновозможными, если вер-ти их наступления равны м/у собой.
Опр. Вер-ти событий, эксперименты кот. можно разложить на равновозможные исходы, равны отношению числа благоприятствующих исходов к общему числу возможных исходов.
 ,
где m
- это число благоприятных событий А,
n
- общее число возможных исходов.
,
где m
- это число благоприятных событий А,
n
- общее число возможных исходов.
Исход наз-ся благоприятствующим событию А, если его появление влечет появление события А.
Формулы
комбинаторики:
1)
Сочетаниями
из n
элементов по m
наз. соединения,
состоящие из m
элементов и отличающихся друг от друга
составом элементов. Число сочетаний
равно числу способов выбора соединений
из m
элементов
из общего числа n
элементов.

2)
Размещениями
из n
элементов по m
наз. соединения, состоящие из m
элементов и отличающиеся друг от друга
либо составом, либо порядком их
следования.

3)
Перестановками из n
элементов наз. соединения, состоящие
из n
элементов и отличающиеся друг от друга
порядком следования элементов.
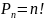
4)Если
в сочетании из n
эл-тов по m
некот. эл-ты повторяются, то их наз.
сочетанием
с повторением:
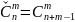
5)Если
в размещениях из n
эл-тов по m
некот. эл-ты повторяются, то их наз.
размещение
с повторением:

4. Геометрическое определение вероятности события.
Согласно геометрич.
схеме опред-ия вер-ти. Вер-ть события,
эксперимент по воспроизведению кот.
можно разложить на бесконечное число
равно возможных исходов, равна отшению
меры благоприятствующей данному событию
области к мере всей области.
 , где
m(G)
– мера
благоприятствующей обл.
, где
m(G)
– мера
благоприятствующей обл.
m(S) – мера всей обл.
В кач-ве меры может выступать длина отрезка, площадь фигуры или объем тела.
В обл. S
появл.
случайная точка. Внутри обл. S
выделяются
замкнутые обл. G1,
G2
и G3,
тогда вер-ть
того, что случайная точка обл. S
окажется в
замкнутых обл. равна:
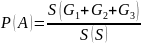
21.Точные законы распред-ия С.В. Распред-ие Стьюдента.
К точным относятся законы распред-ия непрерывных С.В, в формуле плотности распред-ия вер-тей кот. присутствуют только точные значения параметров, но никак ни значения определяемых по статистич. данным.
Пусть мы имеем
С.В. V,
распределенную
по закону
с
n
степенями
свободы. Также задана С.В. Z,
распределенная по закону Гаусса. С.В.
V
и
Z
независимы. Сконструируем из них новую
С.В. T
по формуле:
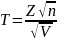
Получившийся в результате исследования закон распределения величины T получил название распред-ие Стьюдента. Ф-ия плотности этого распред-ия имеет вид:
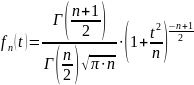
Параметр n обозначает число степеней свободы.
22.Точные законы распред-ия С.В. Распред-ие Фишера-Снедекора.
К точным относятся законы распред-ия непрерывных С.В, в формуле плотности распред-ия вер-тей кот. присутствуют только точные значения параметров, но никак ни значения определяемых по статистич. данным.
Пусть две независим.
С.В. U
и
V
распределены
по закону
со степенями
свободы k1
и
k2
соответственно.
Из этих величин конструируется новая
С.В.
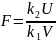 .
.
И![]() сследования
закона распред-ия С.В. F
показало,
что ф-ия плотности этого распред-ия
имеет вид:
сследования
закона распред-ия С.В. F
показало,
что ф-ия плотности этого распред-ия
имеет вид:
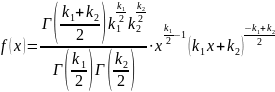
Всегда f(x) > 0
