32. Закон больших чисел. Теорема Бернулли.
В узком смысле закон больших чисел – это ряд теорем, в каждой из кот. устанавливается при тех или иных условиях факт приближения средних характеристик большого числа испытаний к некот. постоянным величинам.
В широком смысле – это некот. общие принципы, согласно кот. совокупное действие большого числа случайных факторов приводит к рез-ту почти независящему от случая, т.е. при большом числе СВ их средний рез-т перестает быть случайным и может быть предсказан с большой степенью определенности.
Теорема Бернулли: Частота события в n повторно-независимых испытаниях, в каждом из кот. оно может наступить с одной и той же вероят-тью p при сходятся по вероят-ти к арифметич. вероят-ти p в наступлении этого события в отдельном испытании.
Док-во: Заключение теоремы вытекает из неравенства Чебышева для частости события при
43. Стат. Гипотеза. Общая схема её проверки. Ошибки 1 и 2 рода.
Стат. гипотеза наз. любое предположение относит-но параметров распределения и самих распределений, полученное в рез-те анализа стат. данных.
Нулевой (основной) гипотезой H0 наз. предположение, кот. мы придерживаемся изначально, пока наблюдения не заставят нас признать обратное.
Альтернативной (конкурирующей) гипотезой H1 наз. гипотеза, кот. противоречит H0 и кот. не отвергается, если отвергается осн. гипотеза.
При проверке гипотез могут быть ошибки двух родов. Ошибка 1-ого рода состоит в том, что осн. гипотеза отвергается, хотя на самом деле она верна. Ошибка 2-ого рода состоит в том, что осн. гипотеза не отвергается, хотя на самом деле она ошибочна.
17. Тип.Зр непр.Случ.Величин. Равномерный закон распределения.
Опр. Непрерыв. С.В. с возмож-ми значениями от a до b, распределена по равномерному закону, если плотность распред-ия её вер-тей задается формулой:
,
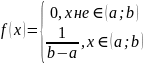где a
и b
– числ.
характ-ки
Теорема.
Числовые харак-ки равномернораспред.
С.В. опред-ся по формулам:
;
;
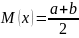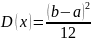Ф-ия распред-ия:
Док-во:
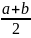
Далее доказать:
и
-∞<x<a, то F(x)= (-∞; x)∫0dx=0
a<x≤b, то F(x)= (-∞;a)∫0dx+ (a;x)∫1/(b-a)dx=(x-a)/(b-a).
b<x<+∞, то F(x)= (-∞;a)∫0dx+ (a;b)∫1/(b-a)dx+(b;x)∫odx=(b-a) /(b-a)=1. Требуемое доказано.
Сфера применения, к примеру: Время ожидания транспорта, С.В. с равном. законом распред. на интервале [0;∆t], где ∆t- интервал дв-ия транспорта.
18. Тип.Зр непр. С.В. Показательный закон распред-ия.
Опр. Непрер.С.В. распределена по показат. закону, если плотность её распред. задается формулой:
Параметром распред-bя явл. λ.
Теорема.
Мат. ожидание, дисперсия и Ƈ, С.В. с
показ-ым законом распред-я:
Ф-ия распред-ия:
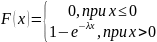
Док-во: M(x)= (-∞;+∞)∫x*f(x)dx=(-∞;0)∫x*0dx+(0;+∞)∫x*λ*e^(-λx)dx=│x=u, du=dx; e^(-λx)dx=dv; v=-(1/λ)*e^(-λx)│=lim(b→+∞)((-x / λ)*e^(- λx)│(0;b) + (0;b)∫(1/λ)*e^(-λx) dx)= lim(b→+∞)(-b*e^(-λb)-(1/λ)*e^(-λx)│(0;b)= lim(b→+∞)(-b/e^(λb) - (1/λ)*(e^(-λb)-1))=1/λ
x≤0, то F(x)= (-∞;x)∫0dx=0
x≥0, то F(x)= (-∞;0)∫0dx+(0;x)∫λe^(-λx)dx=λ*(-1/λ)*e^(-λx)│(0; x)= - (e^(-λx) -1)= 1-e^(-λx). Требуемое доказано.
В сфере массового обслуживания с простейшим потоком событий, время обслуживания заявки имеет показат. закон распред-я.