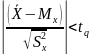- •9. Формула Бернулли и Пуассона.
- •10. Локальная и интегральная теоремы Муавра-Лапласа.
- •11. Способы задания закона распред-ния дискретных св. Их св-ва.
- •12. Способы задания закона распред-ния непрерывных св. Св-ва.
- •29. Закон больших чисел. Неравенство Маркова.
- •30. Закон больших чисел. Неравенство Чебышева.
- •31. Закон больших чисел. Теорема Чебышева.
- •32. Закон больших чисел. Теорема Бернулли.
- •43. Стат. Гипотеза. Общая схема её проверки. Ошибки 1 и 2 рода.
- •17. Тип.Зр непр.Случ.Величин. Равномерный закон распределения.
- •18. Тип.Зр непр. С.В. Показательный закон распред-ия.
- •19. Тип. Зр непр. С.В. Нормальный закон распределения.
- •20. Точные законы распред. С.В. Распред-е Пирсона (хи-квадрат).
- •37. Общие сведения о выборочном методе.
- •38. Точечная оценка параметров распред-ия. Требования к ф-иям выборки.
- •39. Понятие интервальной оценки параметров распред. Доверит. Интервал для неизвестного мат. Ожидания.
- •5. Совместные и несовместные события. Теорема слож-ия вер-тей.
- •7.Полная группа событий. Формула полной вероятности.
- •6. Зависимые и независ. События. Теорема умножения вер-тей.
- •8.Формула Байеса переоценки вер-тей гипотез. Её практич. Значение.
- •25. Плотность вер-ти двумерной с.В.
- •26. Условные законы распределения двумерной с.В.
- •27.Числовые характер-ки двумерной с.В.
- •28. Ковариация и коэффициент корреляции.
- •2. Относительная частота события (очс). Теорема Бернули.
- •3.Классич. Опред-ие вер-ти события. Формулы комбинаторики.
- •4. Геометрическое определение вероятности события.
- •23. Понятие двумерной дискретной св и таблица её распред-ия.
- •24. Функция распред-ия двумерной с.В.
- •41.Понятие интерв-ной оценки параметров распред-ия. Доверит. Интервал для неизвест. Вер-ти для умеренно больших выборок.
- •13. Математич. Ожидание случайных величин. Основные свойства.
- •14. Дисперсия случайных величин. Основные свойства.
- •15. Тип. Законы распред-ия дискрет. C.В. Бином. Закон распред-ия.
- •16. Тип. Законы распред-ия дискретных с.В. Распред-ие Пуассона.
- •34. Интегральная предельная теорема. Теорема Ляпунова.
- •35. Предмет мат. Статистики. Осн. Функция мат. Статистики.
- •36. Основные понятия математической статистики.
- •42. Понятие интерв-ной оценки параметров распред-ия. Доверит. Интервал для неизвест. Вер-ти для малых выборок.
- •45. Проверка гипотезы о равенстве средних двух совокупностей при известных дисперсиях.
- •44. Проверка гипотезы о равенстве средних двух совокупностей при неизвестных дисперсиях.
- •46. Проверка гипотезы о равенстве дисперсий двух совокупностей.
- •45. Проверка гипотезы о равенстве средних двух совокупностей при известных дисперсиях.
- •44. Проверка гипотезы о равенстве средних двух совокупностей при неизвестных дисперсиях.
- •46. Проверка гипотезы о равенстве дисперсий двух совокупностей.
- •47. Гистограмма распред-ия.
- •48. Проверка гипотезы о соответствии эмпирич. Закона распред-ия теоретич.
- •39. Понятие интерв-ной оценки параметров распред-ия. Доверит. Интервал для неизвест. Мат. Ожидания.
- •40. Понятие интерв-ной оценки параметров распред-ия. Доверит. Интервал для дисперсии.
45. Проверка гипотезы о равенстве средних двух совокупностей при известных дисперсиях.
Значение дисперсий
ген. совокуп-ти признака X
и
Y
известны.
Это
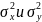 .
.
В кач-ве стат-ки критерия рассматривается

При заданном уровне
значимости
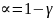 опред-ся критич. Значение распред-ся
Гаусса(
опред-ся критич. Значение распред-ся
Гаусса(
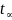 ).
).
а)
если
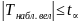 , то осн. гипотеза не отвергается.
, то осн. гипотеза не отвергается.
б)
если
 , то осн. гипотеза
не отвергается.
, то осн. гипотеза
не отвергается.
в)
если
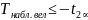 , то осн. гипотеза
не отвергается.
, то осн. гипотеза
не отвергается.
В противном случае во всех 3-х случаях осн. гипотеза отвергается в пользу конкурирующей.
44. Проверка гипотезы о равенстве средних двух совокупностей при неизвестных дисперсиях.
Значение дисперсий ген. совокуп-тей X и Y неизвестны, но они равны м/у собой. Тогда рассматр-ся числ. критерий
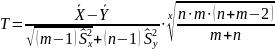
распределенная
по закону Стьюдента со степенями свободы
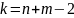 .
При заданной
надежности
в степенях
свободы k
опред-ся
границы критич. точки (
.
При заданной
надежности
в степенях
свободы k
опред-ся
границы критич. точки ( ).
).
а)
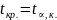 Если
Если
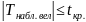 , то H0
–
не отвергается
, то H0
–
не отвергается
б)
 Если
Если
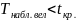 , то H0
–
не отвергается
, то H0
–
не отвергается
в)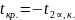 Если
Если
 , то H0
–
не отвергается
, то H0
–
не отвергается
В противном случае H0 отвергается в пользу H1.
46. Проверка гипотезы о равенстве дисперсий двух совокупностей.
Сравнение
дисперсий двух норм. распределенных
ген. совок-тей
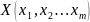 и Y
и Y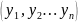 .
.
H0:

H1:
а)
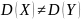 ;
б)
;
б)
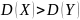 ;
в)
;
в)
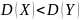 ;
;
Для проверки указанной гипотезы рассмотр. С.В.
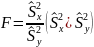
С.В. F
распред-на
по закону Фишера со степенями свободы
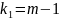 и
и
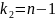 .
.
При заданной надежности опред-ся критич. значение:
а)
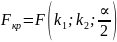
б)
и в)
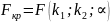
Если
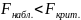 , то нет
оснований отвергать осн. гипотезу. В
противном случае осн. гипотеза отвергается
в пользу конкурирующей на уровне
значимости
, то нет
оснований отвергать осн. гипотезу. В
противном случае осн. гипотеза отвергается
в пользу конкурирующей на уровне
значимости
 .
.
47. Гистограмма распред-ия.
Гистрограмма распред-ия – это ступенчатая фигура состоящая из прямоугольников, ширина кот. равна шагу гистограммы распред-ия, а высота числу элементов или доли элементов выборки, оказавшихся в соответств. интервале гистограммы.
Шаг распростр.
гистограммы:
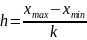 ,
,
где
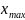 – макс. элемент
выборки;
– макс. элемент
выборки;
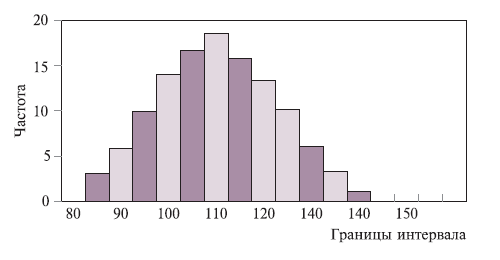
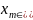 – мин. эл.
выборки;
– мин. эл.
выборки;
48. Проверка гипотезы о соответствии эмпирич. Закона распред-ия теоретич.
Проверяется гипотеза о соответствии эмпирич. закона распред-ия теоретическому.
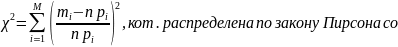
степенями
свободы
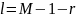 , где
, где
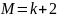 ,
,
k – число разрядов гистограммы;
r – число параметров теоретич. закона распред-ия;
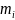 – число эл. выборки,
оказавшихся в i-том
разряде гистограммы;
– число эл. выборки,
оказавшихся в i-том
разряде гистограммы;
 – теоретич. вер-ть
попадания признака X
в i-тый
разряд гистограммы;
– теоретич. вер-ть
попадания признака X
в i-тый
разряд гистограммы;
n – объем выборки;
При заданной
надежности
 опред-ся
границы критич. обл. по табл. распред-ия
Пирсона.
опред-ся
границы критич. обл. по табл. распред-ия
Пирсона.
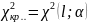
Если
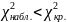 , то можно
утверждать, что признак Х
на уровне
значимости
имеет теоретич.
закон распред-ия.
, то можно
утверждать, что признак Х
на уровне
значимости
имеет теоретич.
закон распред-ия.
39. Понятие интерв-ной оценки параметров распред-ия. Доверит. Интервал для неизвест. Мат. Ожидания.
Опр. Доверит. интервал по данным одной выборки и ориентированный на покрывании им истинного значения параметра с заданной надежностью наз. доверит. интервалом.
Опр. Оценка параметра распред-ия на основе доверит. интервала наз. интервальной оценкой параметра.
Распред-ие Стьюдента:
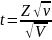 , где z
– С.В., распределенная нормально с мат.
ожиданием = 0 и дисперсией = 1, V
– C.В,
распределенная по закону
с v
степенями
свободы.
, где z
– С.В., распределенная нормально с мат.
ожиданием = 0 и дисперсией = 1, V
– C.В,
распределенная по закону
с v
степенями
свободы.
При построении
доверительного интервала, сделаем
след. подстановки:
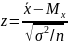 . В кач-ве V
выберем:
. В кач-ве V
выберем:
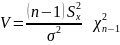 тогда учитывая,
что
тогда учитывая,
что
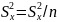 получим
получим
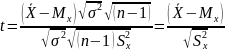
Для того чтобы
построить интервал, в кот с заданной
вер-тью P
лежит истинное значение
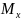 .
.