8. Основные свойства области допустимых решений злп.

Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений.

Чтобы задача (7) - (8) имела решение, системе её ограничений (8) должна быть совместной. Это возможно, если r этой системы не больше числа неизвестных n. Случай r>n вообще невозможен. При r= n система имеет единственное решение, которое будет при оптимальным. В этом случае проблема выбора оптимального решения теряет смысл. Выясним структуру координат угловой точки многогранных решений. Пусть r<n. В этом случае система векторов содержит базис -- максимальную линейно независимую подсистему векторов, через которую любой вектор системы может быть выражен как ее линейная комбинация. Базисов, вообще говоря, может быть несколько, но не более . Каждый из них состоит точно из r векторов. Переменные ЗЛП, соответствующие r векторам базиса, называют, как известно, базисными и обозначают БП. Остальные n - r переменных будут свободными, их обозначают СП. Не ограничивая общности, будем считать, что базис составляют первые m векторов . Этому базису соответствуют базисные переменные , а свободными будут переменные .

Если свободные переменные приравнять нулю, а базисные переменные при этом примут неотрицательные значения, то полученное частное решение системы (8) называют опорным решением (планом).

Теорема. Если система векторов содержит m линейно независимых векторов , то допустимый план (10) является крайней точкой многогранника планов.

Теорема. Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.

9. Правила перехода к двойственной задаче злп.

10. Теоремы двойственности

Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач: можно либо найти оптимальное решение другой задачи, не решая ее, либо установить его отсутствие.

Первая теорема двойственности.

Если одна из двойственных задач имеет оптимальное решение, то двойственная ей задача также имеет оптимальное решение, причем экстремумы целевых функций равны, т.е.

Если одна из двойственных задач не имеет оптимального решения, то другая задача также не имеет оптимального решения, причем если одна из задач не имеет оптимального решения из-за неограниченности целевой функции, то другая из-за несовместности системы ограничений

Вторая теорема двойственности

Для того чтобы допустимые решения и несимметричной пары двойственных задач были соответственно оптимальными решениями, необходимо и достаточно, чтобы для любого j выполнялось равенство

11. Постановка и эмм транспортной задачи лп.

Для решения эконо-х задач математическими методами нужно вначале составить соответствующие им экономико-математические модели (ЭММ). Под ЭММ понимают абстрактное отображение реального экономического процесса в виде математических формул и зависимостей.

Составление ЭММ включает следующие этапы:

1) Определяют искомые величины задачи, т.е ее неизвестные

2) Устанавливают взаимосвязи между неизвестными величинами , с одной стороны, и ограничивающими факторами и условиями, с другой стороны, т.е составляют систему ограничений

3) Выбирают критерий оптимальности (экономи-ий критерий эффективности), называемый целевой функцией, согласно которому из множества допустимых решений определяют наилучшее.

Постановка задачи и ее математическая модель

 Имеется  m  пунктов производства (поставщиков) и n  пунктов

потребления (потребителей) однородного продукта. Заданы величины:

  - объем производства (запас) i-го поставщика,  i=1, m  ;

  - объем потребления   (спрос) j-го потребителя, i=1, n ;

   - стоимость перевозки (транспортные затраты) единицы продукта от i-го поставщика к  j-му потребителю.

            Требуется составить такой план перевозок, при котором спрос

всех потребителей был бы выполнен и при этом общая стоимость всех

перевозок была бы минимальна.

            Математическая модель транспортной задачи имеет вид

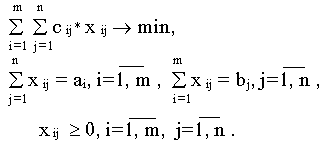
Транспортная задача, в которой суммарные запасы

                                               

и суммарные потребности

                                               

совпадают, называется закрытой моделью;  в противном случае - открытой. Открытая модель решается приведением к закрытой.

            В случае, когда суммарные запасы превышают суммарные

потребности, т.е.

                                               

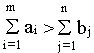
вводится фиктивный n+1 потребитель, потребности которого

                                               

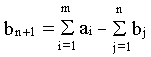
В случае, когда суммарные потребности превышают суммарные

запасы,  т.е.

                                               

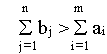
, вводится фиктивный m+1 поставщик, запасы которого

                                               

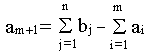
Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика

полагают равными нулю, так как груз в обоих случаях не перевозится.

            Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к

закрытой модели.

Основные свойство транспортной задачи

            Математические модели любых транспортных задач ЛП обладают общими чертами, а именно,

            1) коэффициенты  целевой функции неотрицательны (стоимости перевозок не могут быть отрицательными величинами);

            2) коэффициенты правых частей ограничений неотрицательны (запасы и потребности продукта);

            3) коэффициенты в ограничениях принимают только два значения, это нули и единицы.

            В силу этих особенностей транспортная задача обладает следующими свойствами.