Вычисления определённых интегралов от тригонометрических функций

Пусть функция  — рациональная функция переменных и . Для вычисления интегралов вида у добно использовать формулы Эйлера. Положив, что , и произведя соответствующие преобразования, получим:

.

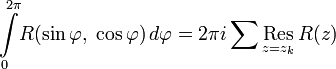
Вычисление несобственных интегралов

Для вычисления несобственных интегралов с применением теории вычетов используют следующие две леммы:

1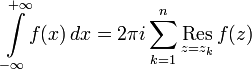 . Пусть функция голоморфна в верхней полуплоскости и на вещественной оси за исключением конечного числа полюсов, не лежащих на вещественной оси и . Тогда 2.-//- и . Тогда

33.Преобразование Лапласа. Связь с преобразованием Фурье.

Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.

П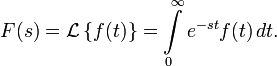 реобразованием Лапласа функции вещественной переменной , называется функция комплексной переменной ^[1], такая что:

Правая часть этого выражения называется интегралом Лапласа.

Обратное преобразование Лапласа

О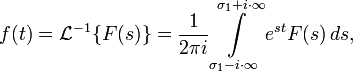 братным преобразованием Лапласа функции комплексного переменного , называется функция вещественной переменной, такая что:

где  — некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.

Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции участвуют значения .

Д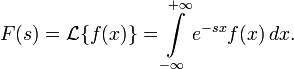 вустороннее преобразование Лапласа определяется следующим образом:

Большим преимуществом преобразования Лапласа является его простая связь с преобразованием Фурье. Для этого необходимо лишь осуществить замену р  j  :

Н епрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом :

Примечание: в этих выражениях опущен масштабирующий множитель , который часто включается в определения преобразования Фурье.

Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.

Прим: s и p одно и то же, было влом переделывать.

3 4.Основные теоремы об оригиналах и изображениях

1 .Линейность: если f(x) -:-F(s) и g(x) -:-G(s), то

2.Умножение на число:

3 .Поведение изображения в бесконечности: если оригинал непрерывен в нуле (в смысле справа от нуля, конечно), то

4. Дифференцирование и интегрирование оригинала

И зображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа:

В более общем случае (производная -го порядка):

И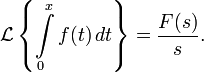 зображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала, делённое на свой аргумент:

• Т 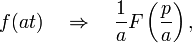еорема подобия

где a>0.

• Дифференцирование оригинала

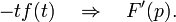
• Д 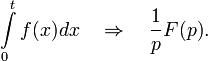ифференцирование изображения

• Интегрирование оригинала

• И 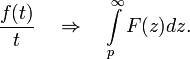нтегрирование изображения

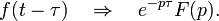
• Т еорема смещения

• Теорема запаздывания