28.Первообразная функции комплексной переменной. Формула Ньютона-Лейбница

Если функция w = f(z) аналитична в односвязной области D, то, как мы доказали, интеграл по кривой зависит только от начальной и конечной точек и не зависти от формы кривой. Если зафиксировать начальную точку z₀, то интеграл будет зависеть только от конечной точки z, поэтому можно написать . Можно доказать (также, как мы доказывали существование потенциальной функции в односвязной области при выполнении условия ∂Q/ ∂x = ∂P/ ∂y), что справедлива следующая         Теорема. Для любой аналитической в области D функции f(z)

интеграл 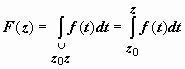является аналитической в D функцией, и F’(z) = f(z).         Любая функция Ф(z) такая, что Ф’(z) = f(z), называется первообразной функции f(z). Любые две первообразные отличаются не более, чем на постоянную, поэтому 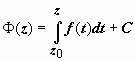, откуда при z = z₀ получаем C = Ф(z₀), или 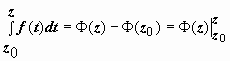. Таким образом, для аналитических функций справедлива формула Ньютона-Лейбница, и основные приёмы интегрирования .      Связь интеграла ФКП и Кри-2

     Сведение интеграла ФКП к интегралу от комплекснозначной функции действительной переменной

     Если то

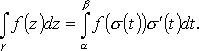
29.Интегральная формула Коши

П усть  — область на комплексной плоскости с кусочно-гладкой границей , функция

регулярна в и  — точка внутри области . Тогда справедлива следующая формула Коши:

Ф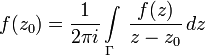 ормула справедлива также, если предполагать, что голоморфна внутри , и непрерывна на замыкании, а также если граница не кусочно-гладкая, а всего лишь спрямляемая.

Доказательство

Рассмотрим окружность достаточно малого радиуса с центром в точке . В области, ограниченной контурами и подынтегральная функция не имеет особенностей и по интегральной теореме Коши интеграл от неё по границе этой области равен нулю. Это означает, что не зависимо от имеем равенство:

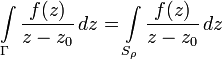
Для расчёта интегралов по применим параметризацию . Сначала докажем формулу Коши отдельно для случая :

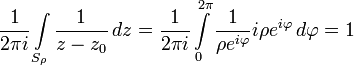
В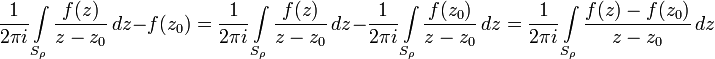 оспользуемся ею для доказательства общего случая:

Так как функция комплексно дифференцируема в точке , то:

Интеграл от равен нулю:

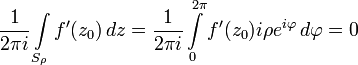
Интеграл от члена может быть сделан сколь угодно мал при . Но поскольку он от вообще не зависит, значит он равен нулю. В итоге получаем, что

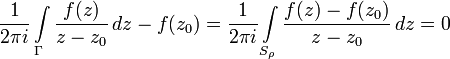
30.Ряд Лорана

Ряд Лорана — двусторонне бесконечный степенной ряд по целым степеням , то есть ряд вида

Э тот ряд понимается как сумма двух рядов:

1.  — положительная часть ряда Лорана (иногда называется правильной) и

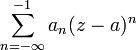
2.  — отрицательная часть ряда Лорана (иногда называется главной).

При этом ряд Лорана считается сходящимся тогда и только тогда, когда сходятся его правильная и главная части. Термин назван в честь французского математика П. А. Лорана.

Свойства

Если внутренность области сходимости ряда Лорана непуста, то она представляет собой круговое кольцо

• Во всех точках своего кольца сходимости ряд Лорана сходится абсолютно;

• Как и для степенных рядов, поведение ряда Лорана в точках граничных окружностей кольца сходимости может быть самым разнообразным;

• На любом компактном подмножестве ряд сходится равномерно;

• Сумма ряда Лорана в есть аналитическая функция ;

• Ряд Лорана можно дифференцировать и интегрировать в почленно;

• Разложение в ряд Лорана единственно, то есть если суммы двух рядов Лорана совпадают в , то совпадают и все коэффициенты этих рядов.

• Коэффициенты 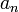ряда Лорана определяются через его сумму формулами

г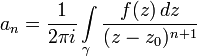 де , ,  — любая окружность с центром a, расположенная внутри кольца сходимости.