25.Понятие конформного отображения

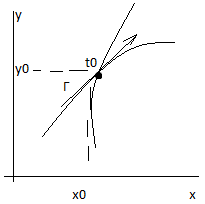
Линия Г на плоскости комплексного переменного z описывается при помощи уравнения: Г: z=z(t)=x(t)+y(t),

L<=t<=B (1).

Т е с помощью 2х параметрических вещественных уравнений x=x(t) и y=y(t)

Производная комплексной функции z вещественного параметра t при t=t0, L<=t<=B определяется как

(2)

Формула 2 доказывает, что если z’(t0) существует и U!=0, то этот комплексный вектор направлен по касательной кривой Г в точке z0=z(t0)=x0+iy(t0)

Определение: кривая называется гладкой, если функция z(t) непрерывна и имеет непрерывную производную z’(t) причем всюду z’(t)!=0 L<=t<=B

При t=L и t=B подразумеваются односторонние производные

Кривая называется кусочно-гладкой, если она непрерывно составлена из конечного числа гладких кривых.

26.Понятие интеграла функции комплексного переменного и его свойства

Пусть -- определена и однозначна в области

Рассмотри кривую . -- гладкая с началом в точке и с концом в точке

М ы точками разобьём кривую на элементарные дуги

-- длина -й ломаной

Определение: если при не зависящее от разбиения и выбора точек , то предел будем называть

Если непрерывно в области , то наш интеграл существует

Будем обозначать точки не , а (для удобства)

Как считать интеграл :

П усть

М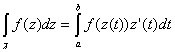 ожно по формуле Грина, но обычно параметризуя кривую, сводим к обычному интегралу Римана

Например, если , то

1 )

2 ) Линейность интеграла:

3) Аддитивность: пусть , тогда

4) Если -- длина , а , то

27.Теорема Коши для односвязной и многосвязной области

Т еорема Коши для односвязной области. Если D - односвязная ограниченная область, w = f( z) - аналитическая в этой области функция, то для любого кусочно-гладкого замкнутого контура L, лежащего в D, интеграл от f(z) по L равен нулю: .         

Доказательство. эта важнейшая теорема непосредственно следует из условий Коши-Римана и формулы Грина. Так как, по доказанному выше, , то, применяя к действительным криволинейным интегралам формулу Грина, получим 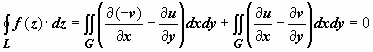в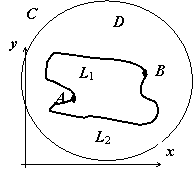 следствие условий Коши-Римана . Символом G в доказательстве обозначена область, заключённая внутри контура L.         Следствие. Для всех кусочно-гладких кривых, лежащих внутри области D, в которой аналитична функция w = f(z), и имеющих общие начальную и конечную точки, интеграл имеет одинаковое значение.         Доказательство полностью повторяет доказательство Теоремы 1 раздела 16.3.3.5.1. Объединение L₁∪L₂⁻ кривых - замкнутый контур, поэтому 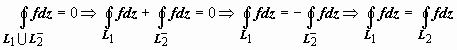.         Оказывается, что справедлива и обратная теорема Морера: если функция w = f(z) непрерывна в односвязной области D и интеграл по любому замкнутому кусочно-гладкому контуру, лежащему в D, равен нулю, то функция аналитична в области D.

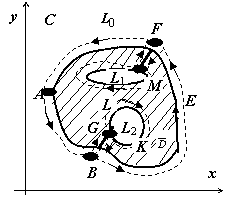Теорема Коши для многосвязной области. Если функция w = f(z) аналитична в замкнутой многосвязной ограниченной области , ограниченной контурами L₀ (внешняя граница), L₁, L₂, …, L_k, то интеграл от f(z), взятый по полной границе области , проходимой так, что область остаётся с одной стороны, равен нулю.         Доказательство и здесь воспроизводит доказательство формулы Грина для многосвязной о бласти. Рассмотрим случай, когда граница области (на рисунке область заштрихована) состоит из внешнего контура L₀ и внутренних контуров L₁ и L₂. Соединим контур L₀ разрезом FM с контуром L₁, разрезом BG - с контуром L₂. Область с границей односвязна, поэтому для неё справедлива интегральная теорема Коши: . Интегралы по каждому из разрезов входят в этот общий интеграл дважды в противоположных направлениях и, как следствие, взаимно уничтожаются, поэтому остаются только интегралы по контурам, проходимым так, что область остаётся с одной стороны.         В дальнейшем нам понадобится другая формулировка этой теоремы. Буквами без верхнего индекса будем обозначать контуры, проходимые против часовой стрелки, с верхним минусом - по часовой. Мы доказали, что . Таким образом, интеграл по внешнему контуру равен сумме интегралов по внутренним контурам, при этом все контуры обходятся в одном направлении.