
- •23.Дифференцирование функции комплексного переменного. Теорема Коши-Римана Определение
- •1 . Необходимость
- •2. Достаточность
- •25.Понятие конформного отображения
- •26.Понятие интеграла функции комплексного переменного и его свойства
- •27.Теорема Коши для односвязной и многосвязной области
- •28.Первообразная функции комплексной переменной. Формула Ньютона-Лейбница
- •29.Интегральная формула Коши
- •Доказательство
- •30.Ряд Лорана
- •Свойства
- •Теорема Лорана
- •31. Изолированные особые точки
- •Критерии устранимости
- •32.Вычеты и их применение
- •Вычисления определённых интегралов от тригонометрических функций
- •Вычисление несобственных интегралов
- •33.Преобразование Лапласа. Связь с преобразованием Фурье.
- •Обратное преобразование Лапласа
- •3 4.Основные теоремы об оригиналах и изображениях
- •35.Свертка оригиналов
- •36.Применение операционного исчисления
- •3 7.Вычисление оригиналов по известному изображению
23.Дифференцирование функции комплексного переменного. Теорема Коши-Римана Определение
П![]() роизводная
для комплексной функции одного аргумента
роизводная
для комплексной функции одного аргумента
![]() определяется
так же, как и для вещественной: (здесь
определяется
так же, как и для вещественной: (здесь
![]() —
комплексное число). Если этот предел
существует, функция называется
дифференцируемой или голоморфной.
При этом
—
комплексное число). Если этот предел
существует, функция называется
дифференцируемой или голоморфной.
При этом
![]()
Следует учитывать одну важную особенность:
поскольку комплексная функция задана
на плоскости, существование приведённого
предела означает, что он одинаков при
стремлении к
![]() с
любого направления. Этот факт накладывает
существенные ограничения на вид
функций-компонент
с
любого направления. Этот факт накладывает
существенные ограничения на вид
функций-компонент
![]() и
определяет их жёсткую взаимосвязь через
Т Кощи-Римана: Для того чтобы функция
и
определяет их жёсткую взаимосвязь через
Т Кощи-Римана: Для того чтобы функция
![]() ,
определённая в некоторой области
,
определённая в некоторой области
![]() комплексной
плоскости, была дифференцируема в точке
комплексной
плоскости, была дифференцируема в точке
![]() как
функция комплексного переменного
,
необходимо и достаточно, чтобы её
вещественная и мнимая части
как
функция комплексного переменного
,
необходимо и достаточно, чтобы её
вещественная и мнимая части
![]() и
и
![]() были
дифференцируемы в точке
были
дифференцируемы в точке
![]() как
функции вещественных переменных
как
функции вещественных переменных
![]() и
и
![]() и
чтобы, кроме того, в этой точке выполнялись
условия Коши — Римана:
и
чтобы, кроме того, в этой точке выполнялись
условия Коши — Римана:
Е![]()
![]() сли
условия Коши — Римана выполнены, то
производная
сли
условия Коши — Римана выполнены, то
производная
![]() представима
в любой из следующих форм:
представима
в любой из следующих форм:
Доказательство
1 . Необходимость
По условию теоремы существует предел ,
не зависящий от способа стремления
![]() к
нулю. Положим
к
нулю. Положим
![]() и
рассмотрим выражение
и
рассмотрим выражение
![]() .
.
И![]()
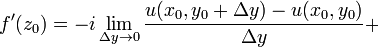 з
существования предела комплексного
выражения следует существование
действительной и мнимой его частей.
Поэтому в точке
з
существования предела комплексного
выражения следует существование
действительной и мнимой его частей.
Поэтому в точке
![]() существуют
частные производные по x функций u(x,y) и
v(x,y) и имеет место формула
существуют
частные производные по x функций u(x,y) и
v(x,y) и имеет место формула
Полагая
![]() ,
находим
,
находим
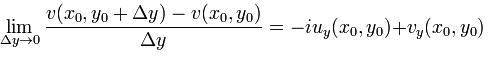
Сравнивая две последние формулы, убеждаемся в справедливости условий Коши-Римана.
2. Достаточность
По определению дифференцируемости,
приращения функций
![]() и
и
![]() в
окрестности точки
в
окрестности точки
![]() могут
быть записаны в виде
могут
быть записаны в виде
![]() ,
,
![]() ,
,
где функции
![]() и
и
![]() стремятся
к нулю при
стремятся
к нулю при
![]() ,
,
![]() быстрее,
чем
быстрее,
чем
![]() и
и
![]()
![]() ,
,
![]() ,
,
![]() .
Составим теперь разностное соотношение
.
Составим теперь разностное соотношение
![]() ,
где
,
где
![]() и
преобразуем его к виду
и
преобразуем его к виду
![]()
![]() .
.
Заметим, что при стремлении
к
нулю последнее слагаемое этой формулы
стремится к нулю, а первые остаются
неизменными. Поэтому существует предел
![]() ,
что и доказывает дифференцируемость
функции
,
что и доказывает дифференцируемость
функции
![]() в
точке
в
точке
![]() .
.
24. Аналитическая функция комплексной
переменной.функция комплексного
переменного
![]() (где
(где
![]() и
и
![]() —
вещественнозначные функции комплексного
переменного, являющиеся, соответственно,
вещественной и мнимой частью рассматриваемой
функции), для которой в каждой точке
некоторой области
—
вещественнозначные функции комплексного
переменного, являющиеся, соответственно,
вещественной и мнимой частью рассматриваемой
функции), для которой в каждой точке
некоторой области
![]() ,
называемой областью аналитичности,
выполняется одно из трёх равносильных
условий:
,
называемой областью аналитичности,
выполняется одно из трёх равносильных
условий:
1![]()
![]() .Для
вещественной и мнимой части этой функции
в каждой точке
.Для
вещественной и мнимой части этой функции
в каждой точке
![]() выполняются
условия
Коши — Римана (аналитичность
в смысле Коши — Римана);
выполняются
условия
Коши — Римана (аналитичность
в смысле Коши — Римана);
2.Ряд
Тейлора функции в каждой точке
![]() сходится
и его сумма равна
(аналитичность
в смысле Вейерштрасса);
сходится
и его сумма равна
(аналитичность
в смысле Вейерштрасса);
3.Интеграл
![]() для
любой замкнутой кривой
для
любой замкнутой кривой
![]() (аналитичность
в смысле Коши)
(аналитичность
в смысле Коши)
Свойства
Арифметические свойства
Если
и
![]() аналитичны
в области
аналитичны
в области
![]()
Функции
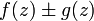 ,
,
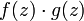 и
и
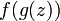 аналитичны
в
аналитичны
в
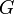 .
.Если в области не обращается в ноль, то
 будет
аналитична в
будет
аналитична в
Если
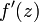 в
области
не
обращается в ноль, то
в
области
не
обращается в ноль, то
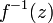 будет
аналитична в
.
будет
аналитична в
.
Аналитическая функция бесконечно дифференцируема в своей области аналитичности. Обратное в общем случае неверно.
