43. Уравнение адиабаты идеального газа.
Адиабатным называют процесс, происходящий без теплообмена с внешней средой.
Уравнение
адиабаты
в координатах ТV:
уравнение Пуассона.
-
показатель адиабаты.
44.Политропические процессы.
Политропическим
называется процесс, при котором
теплоемкость тела остается постоянной.
Уравнение политропы
идеального газа для случая
:
Уравнение политропы
идеального газа для случая:
Если
изобарный.
Если
изотермический.
Если
адиабатный
Если
изохорный.
45. Ван-дер-ваальсовский газ.
Уравнение
Ван-дер-Ваальса:
где
-молярный
объем, р
– давление оказывающее на газ из вне,
а,b
– константы, имеющие для разных газов
различные значения.
Внутренняя энергия В-д-В должна включать в себя кроме кинетической энергии молекул так же энергию взаимодействия между молекулами:
Для одного моля:
Для газа произвольной
массы:
46. Давление газа на стенку сосуда. Средняя энергия молекул.
Давление,
создаваемое на дно и стенки сосуда
столбом жидкости или газа можно посчитать
по формуле:
,
где
- плотность жидкости или газа, h
– высота столба жидкости или газа, g
– ускорение свободного падения.
Средняя кинетическая
энергия поступательного движения
молекулы:
где k
– постоянная Больцмана.
Средняя полная
кинетическая энергия молекулы:
где i
– число степеней свободы молекулы.
47. Распределение Максвелла.
Распределение Максвелла:
или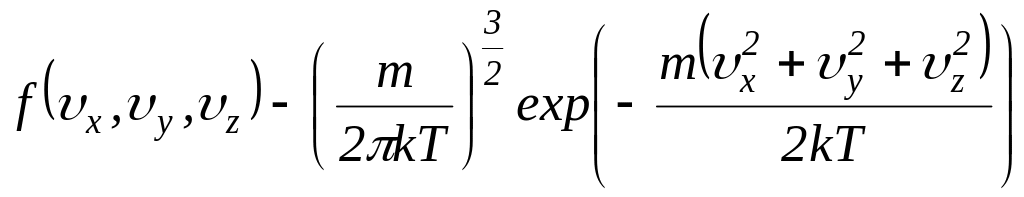
Кроме полученного
выше распределения Максвелла часто при
проведении расчетов используется
распределение по абсолютным значениям
скоростей молекул газа. Для получения
этого распределения запишем в общем
виде вероятность того, что значения
проекций скорости лежат внутри
элементарного объема пространства
скоростей:
:
Учитывая то, что
эта вероятность зависит только от
величины скорости и не зависит от её
направления в пространстве, элементарный
объем
можно считать имеющим форму шарового
слоя со средним радиусом v
и толщиной dv.
Указанная возможность связана с тем,
что в любой точке на поверхности сферы,
центр которой совпадает с началом
координат пространства скоростей,
значения скорости
,
а следовательно и функции
,
одинаковые. Считая шаровой слой тонким,
и записывая его элементарный объем в
виде:
,
выражение может быть представлено в
форме 
.
Функция
или
называется функцией распределения
Максвелла по абсолютным значениям
скоростей,
и она показывает вероятность того, что
величина скорости имеет значения от
до
.
48. Распределение Больцмана.
,
где
-
концентрация газа в точке, соответствующей
началу координат при условии, что
.
Формула была впервые получена в 1866 году Л. Больцманом и описывает распределение, получившее название распределения Больцмана. Это распределение позволяет рассчитывать концентрацию газа, находящегося в равновесном состоянии во внешнем силовом поле. Причем это поле не должно быть обязательно гравитационным, а может иметь любое происхождение, в частности, быть электростатическим или полем сил инерции.
Анализ
распределения Больцмана показывает,
что концентрация молекул газа тем выше,
чем меньше их потенциальная энергия.
Кроме этого, с понижением температуры
увеличивается отличие концентраций в
точках с различными значениями
потенциальной энергии молекул. А при
стремлении температуры к абсолютному
нулю, молекулы начинают скапливаться
в месте, где их потенциальная энергия
принимает наименьшее значение. Указанные
особенности распределения Больцмана
являются следствием теплового движения
молекул, так как кинетическая энергия
их поступательного движения в среднем
равна
и уменьшается пропорционально уменьшению
температуры. А уменьшение кинетической
энергии приводит к уменьшению количества
молекул, способных преодолеть потенциальный
порог, высота которого характеризуется
величиной потенциальной энергии высотой
.