31. Законы сохранения для различных видов соударений.

Абсолютно упругий удар:

Абсолютно неупругий удар:

32. Линии и трубки тока. Неразрывность струи.

Движение жидкостей называется течением, а совокупность частиц движущейся жидкости – потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводят так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства. Линии тока проводят так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т.е. можно определить состояние движения жидкости. Линии тока в жидкости можно "проявить", например, подмешав в нее какое-либо заметные взвешенные частицы.

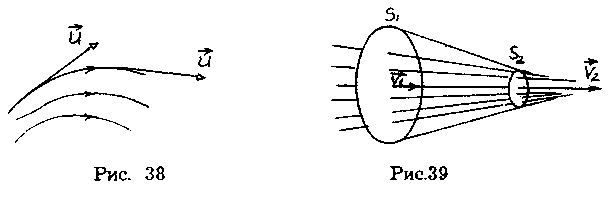
Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.

Рассмотрим какую-либо трубку тока. Выберем два ее сечения S₁ и S₂ , перпендикулярные направлению скорости.

За время Dt через сечение S проходит объем жидкости ; следовательно, за 1 с через S₁ пройдет объем жидкости S₁ , где - скорость течения жидкости в месте сечения S. Через сечение S₂ за 1 с пройдет объем жидкости S₂ , где - скорость течения жидкости в месте сечения S₂. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема, то через сечение S₁ пройдет такой же объем жидкости, как и через сечение S₂ т.е: S₁ = S₂ =const.

Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение называется уравнением неразрывности для несжимаемой жидкости.

33. Уравнение Бернулли.

Уравнение Бернулли: Полное давление жидкости, равно сумме: динамического , гидростатического и статического р давлений является постоянной величиной. + + р = const (Наклонные трубы).

+ р =const для горизонтальных труб.

34. Силы внутреннего трения. Вязкость.

Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее - увеличивается, что приводит к торможению слоя , движущегося быстрее , и ускорению слоя, движущегося медленнее.

Сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона: , где h - динамическая вязкость (вязкость), - градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев, S -площадь, на которую действует сила F.

Взаимодействие двух слоев согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе. Тогда можно записать: , где - плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х; - градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости.

Динамическая вязкость h численно равна плотности потока импульса при градиенте скорости равном единице; она вычисляется по формуле .

Зависимости между l, D и h: .