4. Атомы щелочных металлов

В некотором смысле атомы щелочных металлов являются водородоподобными, однако не полностью. Дело в том, что внешний электрон деформирует электронный остов и тем самым искажает поле, в котором движется. В первом приближении поле остова можно рассматривать как суперпозицию поля точечного заряда +е, и поля точечного диполя, расположенного в центре остова. При этом ось диполя направлена все время к внешнему электрону. Поэтому движение последнего происходит так, как если бы поле остова, несмотря на искажение, сохранялось сферически симметричным.

Это позволяет представить потенциальную энергию внешнего электрона в поле такого остова как:

U(r) = -e²/r – Ce²/r², (6.18)

где С – некоторая постоянная.

Решение УШ для электрона с потенциальной энергией (6.18) приводит к тому, что теперь разрешенные состояния энергии Е в области E < 0 (для связных состояний внешнего электрона) будет зависеть не только от главного квантового числа n (как в случае атома водорода), но и от орбитального квантового числа l:

E_nl = -ћR/(n + _l)², (6.19)

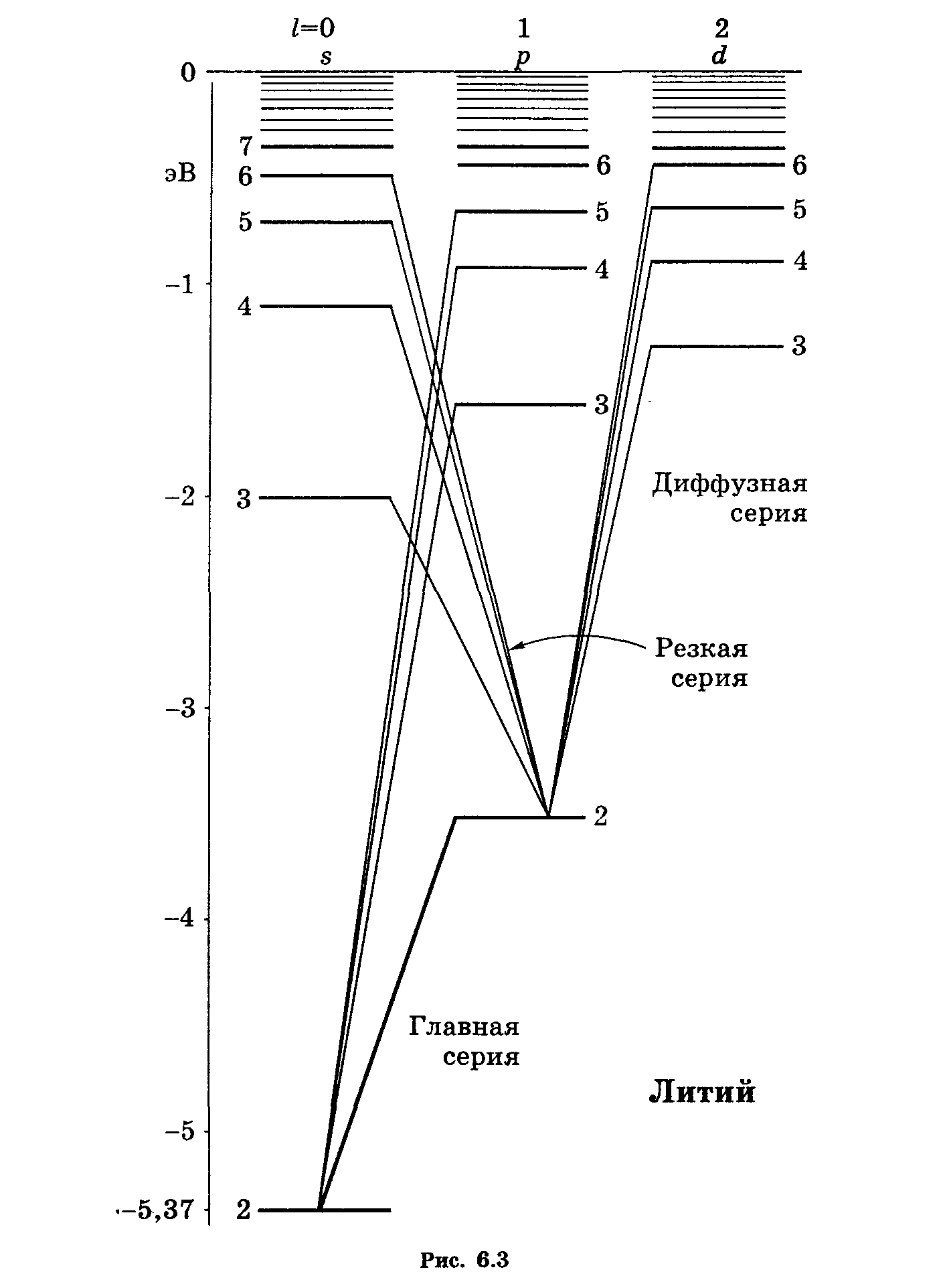
где _l) – ридберговская поправка (или квантовый дефект), зависящая от l . Заметим, ц лития (см. рис. 6.3) основным состоянием является 2s , так как состояние с n = 1 уже занято двумя электронами, входящими в состав остова.

Энергетическому уровню (6.19) соответствует терм, имеющий согласно 2.30 вид:

T_nl = R/(n + _l)² (6.20).

Систематику энергетических уровней атома принято назвать системой термов. Терм T – это величина, определяемая согласно  = R(1/n_o² – 1/n²) (2.16) и E_n = -me⁴Z²/2ћ²n² (2.25) как:

T_n = R/n² = |E_n|/ћ,

где R – постоянная Ридберга. В отличие от энергии E_n, терм - величина положительная, и чем выше уровень, тем больше его значение. Терм имеет ту же размерность, что и частота , т.е. с^-1. Соответствующая частота фотона, испущенного при переходе атома из состояния с квантовым числом n₁ в состояние с квантовым числом n₂, определяется формулой:

₁₂ = T₂ – T₁ = R/n₂² – R/n₁². (2.31)

Все серии хххх представляются в виде обобщенной формулы Бальмера:

 = R(1/n_o² – 1/n²) (2.16).

Энергия E_n электрона на n-й стационарной орбите определяется формулой

E_n = -me⁴Z²/2ћ²n² (2.25).

1.4.х. Найти ридберговскую поправку 3Р терма атома Na , первый потенциал возбуждения которого ₁ = 2,10 В, а энергия связи валентного электрона в основном 3S- состоянии Е_о = 5,14 эВ.

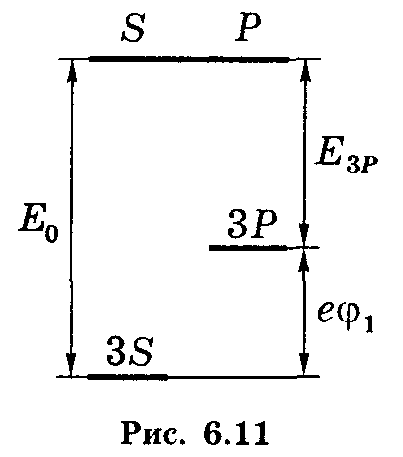
1.4.х. Используем формулу E_nl = -ħR/(n + _l)² (6.19), которая содержит искомую поправку _P. Согласно рис. 6.11. энергию 3Р – состояния можно представить как:

E_3P = -(E_o – e₁) = -(5,14 – 2,19) эВ (имея в виду, что энергия уровня равна с обратным знаком энергии связи на этом уровне). Таким образом, имеем:



1.4.х. Найти энергию связи валентного электрона в основном состоянии атома лития, если известно, что длины волн головной линии резкой серии и ее коротковолновой границы равны соответственно ₁ = 813 нм и _K = 350 нм.

1.4.х. Согласно формуле E_nl = -ħR/(n + _l)² энергия связи в 2s- состоянии равна:

Задача сводится к нахождению поправки _s. Из рис. 6.3 и формулы 6.19 можно записать:

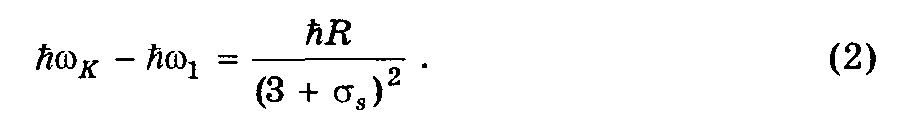
Т.к.  = 2c// перепишем (2) как:

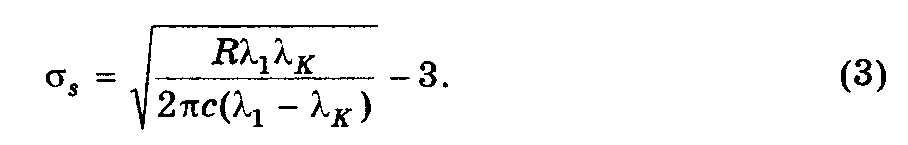
Подставив (3) в (1) получим: E_св = ћR/[(R₁_K/2c)^1/2 - 1]² = 5,3 эВ, где  = ₁ –_K.