6.1Общая задача и классические модели дискретного программирования.
Дискретное программирование-такой раздел математики, который изучает задачи вида f(x)→extr(1), x€GcR^n(2), где G – дискретное множество.
К задаче дискретного программирования сводятся многие прикладные задачи: задачи размещения производства, оптимизации компонентов средств доставки груза, оптимизация проектирования, оптимизации учебный расписаний, синхронизации сигналов уличного движения и др.
Рассмотрим классические задачи дискретного программирования
1)задача о рюкзаке
Емкость v и n видов неделимых предметов со стоимостью c1, c2...Cn и емкостью a1,a2..An соответственно. Необходимо загрузить рюкзак этими предметами так чтобы суммарная стоимость предметов была максимальной
f(x)=c1x1+c2x2+..+CnXn→max
a1x1+..+AnXn≤b
Xj≥0, j=1,n; Xj – целое j=1,n
2) задача о комми-вояжоре(бродячем торговце)
n- городов, C=(Cij)n*m, Cij - расстояние между городами
Торговец должен побывать в каждом городе по 1 разу и вернуться обратно в 1ый город.В каком порядке следует объезжать города чтобы суммарное расстояние было минимальным
Xij=(1,
торговец из i
в j),
(0, в противном случае );
Cij*Xij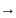
min
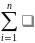Xij=1,
j=1,n
-город в который приезжает,
Xij=1, j=1,n город в который отъезжает
Условие что путь торговца состоит из 1 замкнутого цикла, где Ui могут принимать различные значения Ui-Uj+NXij≤n-1, U-путь
6.2 Задача целочисленного программирования и её решение методом Гомори. Задачей цлп наз задача вида
f(x)=(n,j=1)∑cjxj (max)(1)
(n,j=1)∑aijxj≤bi, i=1,m(2)
xj≥=0, j=1,n(3)
xj-целое, jεJεN(4)
где N-множество индексов 1,2,…,n
Если J=N(на все переменные накладывается условие целочисленности), то задача (1-4) называется полностью ЦЗЛП, в противном случае – частично ЦЗЛП.
Задачу (1-4) можно интерпретировать как задачу об оптимальном производстве неделимых видов продукции.
Одним из методом решения задачи (1-4) явл метод Гомори. Он относится к групе методов, называемых методами отсечения.
Рассмотрим суть метода Гомори для случая J=N:
отбрасывается условие целочисленности (4)
получившуюся ЗЛП решают симплекс-методом. Если оптимальный план задачи (1-3) удовлетворяет условию целочисленности(4), то он является оптимальным планом и для задачи (1-4)
если получен нецелочисленный план, то к ограничениям задачи (1-4) добавляют дополнительное линейное ограничение, обладающее свойствами:
- 1)оптим нецелочис план ему не удовлетворяет
2)любой целочисленный план ему удовлетворяет
решается расширенная задача. Процесс повторяется до получения оптимального плана.
Замечание: если в качестве решения принимать округленные решения, то это решение может оказаться далеким от оптимального.
Геом интерпретация идеи методов отсечения состоит в следующем:
Дополнительное линейное ограничение представляет собой гиперплоскость, которая отсекает часть многогранника планов с оптимальной нецелочисленной вершиной, но при этом не затрагивает ни одной целой точки.
Дополнительное ограничение со свойствами 1,2 наз правильным отсечением.
Целой частью числа [x] наз наиб целое число, не превосходящее х.
Дробной частью числа {x} наз число равное x-[x]
Теорема от отсечении
Если x*k-нецелочисленная компонента оптимального плана х*, то соотношения
xn+1=-{x*k}+(n-m,j=1)∑{αk,m+j}xm+j (10)
xn+1>=0
задают правильное отсечение.
Замечание: если в оптимальном плане х* имеется несколько нецелочисленных компонент, то для построения правильного отсечения выбирают компоненту с наибольшей дробной частью.
Для частично целочисленной задачи правильное отсечение имеет другой вид
Отсечение наз отсечением Гомори