1.1.Опр.1. Экономико-математическая модель — это представление наиболее существенных экон-х взаимосвязей, исследуемых экон-х объектов или процессов в виде системы неравенств, уравнений и т.д.

Матем-я модель, рассматр-я в мат программ-и, представл собой экстремальную или оптимизационную задачу.

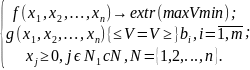(1-3)

Опр.2. Мат. прог. —раздел математики, в к-м решаются экстремальные задачи вида 1-3 и разрабатываются методы их решения.

Задача 1-3 наз общей задачей мат прогр-я.

Опр.3. Числовой набор переменных (x₁, x₂,…, x_n), удовлетворяющий ограничениям (2, 3) задачи 1-3, наз. планом этой задачи.

Опр.4. План, на к-м достигается экстремум целевой функции (1), наз. оптимальным планом задачи 1-3.

В завис-ти от св-в функ-и f_i и g_i матем прогр-е распадается на ряд разделов. Если все функции линейны, то соответ-й раздел наз. линейным прогр-ем. А если хотя бы одна из них не линейна, то говорят о нелинейном прошр-и (дробнолин-е, выпуклое, параметрическое, динамическое).

2.2 Общей задачей лп наз. Задачи вида:

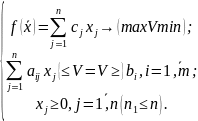
Где c_j , b_i , a_ij — некоторые числа. Можно записать без знака суммы:

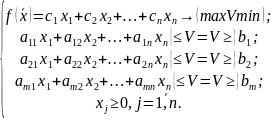
Кроме того задачу 1-3 м/записать в векторно-матричном виде. Для этого введем обозначения:

— вектор коэф-в целевой функции;

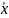— вектор неизвестных переменных;

А — матрица коф-в при переменных основных ограничений;

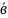— вектор свободных членов.

Тогда задача 1-3 запишется в векторно-матричном виде:

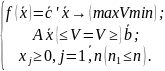
Опр.1. Если в задаче 1-3 целевая функция максимизируется, а в ограничениях (2) знаки сравнения имеют вид (≤) или целевая функция минимизируется, а знаки сравнения в ограничениях (2) имеют вид только (≥) и n₁=n, то говорят, что задача записана в симметричной форме записи.

Опр.2. Если в задаче 1-3 в ограничении (2) используются только знаки сравнения (=), а n₁=n, то говорят, что задача 1-3 записана в канонической форме записи.

Во всех остальных случаях говорят, что задача записана в произвольной форме записи.

Часто при решении ЗЛП возникает необходимость перехода от одного вида записи к другому, эквивалентному ей.

Такой переход осущ-ся на основ-и след теоремы и некоторых факторов.

Теорема 1. Всякому реш-ю α₁,α₂, … , α_п неравенства а₁х₁+а₂х₂+…+а_пх_п ≤ а соответствует одно вполне определенное реш-е α₁,α₂, … , α_п,α_п+1 системы:

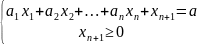
Очень часто вместо задач на минимум удобно решать задачи на максимум. Переход от задачи на мин к задаче на мах осуществляется на основании равенства:

.

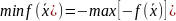Если на некоторой переменной х_к нет условия неотрицательности, тогда ее можно заменить разностью двух других переменных х_k^’ и x_k^’’ на которые накладывается условие неотрицательности.

2.3 Геометрическая интерпретация злп.

Всякий набор переменных (x₁, x₂,…, x_n) м/рассматривать как точку n-мерного пространства. Тогда множество планов ЗЛП 1-3 м/рассматривать как множество точек n-мерного пространства.

Теорема 2. Множество планов общей ЗЛП явл выпуклым многогранным множеством.

Множество наз. выпуклым если вместе с любыми своими двумя точками оно содержит и отрезок их соединяющий. Точки отрезка описыв след равенством:

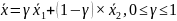
Доказательство (при n=2):

Задача 1-3 примет вид:

(6)

Каждое неравенство в зад (6) описывает полуплоскость причем для i-го неравенства полуплоскость ограничена прямой 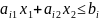. Полуплоскости явл выпуклыми множествами. Пересечения выпуклых множеств также явл выпуклвми множ-ми. Т.о. множ-во планов задачи (6) явл выпуклым, т.к. оно представляет собой пересечение множ-ва полуплоскостей. А т.к все полуплоскости зад (6) ограничены прямыми, то оно явл выпуклым многогранным множеством.

Опр.3. Линией уровня функции наз геометрическое место точек, для к-х значение функции есть величина постоян.

Тогда для целевой функ-и в зад (6) геометр место точек будет описыв уравнением 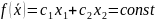(7). Урав-е (7) описывает множ-во параллельн прямых, задаваемых значением константы и перпендикулярны вектору . Вектор наз вектором-градиентом функ-и. Он показыв-т направление возрастания функ-и. Вектор наз вектором-антиградиентом. Он показыв-т направление убывания функции.

Геометр интерпретация ЗЛП базируется на осн теореме ЛП. Теорема 3. Линейн функ-я, определяемая на выпуклом многогранном множестве, достигает своего экстремума в вершине этого множества и если она достигает экстремума более чем в одной вершине, то она достигает такого же значения в любой точке, к-я явл-ся выпуклой линейной комбинацией этих вершин.

Учитывая теор 3 дадим геометр интерпретацию ЗЛП. Требуется найти вершину многогранника планов, через к-ю проходит линия уровня целев функ-и с ее самым большим значением (если зад реш на макс) и найти вершину многогранника планов, через к-ю проходит линия уровня целев функ-и с ее самым меньшим значением (если на миним).

Из геометрич интерпретации следует графический метод ее реш-я. Алгоритм реш-я ЗЛП графич методом:

1) Построить многогранник плана.

2) Построить вектор-градиент целев функ-и. Он имеет начало в начале координат, а конец в точке с координатами с₁ и с₂.

3) Строим какую-либо линию уровня целев функ-и, перпендикулярную вектору-градиенту.

4) Если требуется найти максимум целев функ-и, то перемещаем линию уровня параллельно самой себе в направлении вектора-градиента до тех пор пока не найдем самую удаленную вершину. В этой вершине будет достигаться мах целевой функ-и.

5) Если требуется найти минимум целев функ-и, то перемещаем линию уровня параллельно самой себе в направлении противоположном вектору-градиенту до тех пор пока не найдем самую удаленную вершину. В этой вершине будет достигаться минимум целевой функ-и.

6) Находим координаты оптимальной вершины: для этого составляем систему из уравнений прямых, пересекающихся в оптимальной вершине, и решаем ее.

7) Даем эконом интерпретацию результатам.