2.2. Показательное распределение

Говорят, что НСВ Х имеет показательное (или экспоненциальное) распределение, если

Или, короче .

Положительная величина называется параметром показательного распределения. График показательного распределения имеет вид:

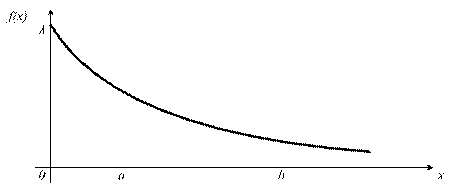
Рисунок 5.14

,

.

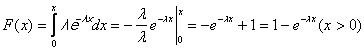График функции распределения имеет вид:

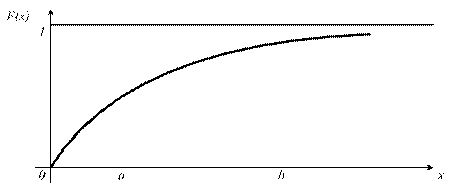
Рисунок 5.15

 

Показательное распределение играет большую роль в теории марковских случайных процессов, теории массового обслуживания и теории надежности. Дискретным аналогом экспоненциального распределения является геометрическое распределение.

Экспоненциально распределенная СВ Х обладает важным свойством: отсутствием последействия. Отсутствие последействия является характеристическим свойством экспоненциально распределенных случайных величин. Экспоненциальное распределение тесно связано с распределением Пуассона, а именно: если времена между последовательными наступлениями некоторого события представляют собой независимые (определение независимости случайных величин будет дано позже) экспоненциально распределенные (с одним и тем же параметром ) случайные величины, то число наступлений этого события за время t распределено по закону Пуассона с параметром λt.

 

2.3. Нормальное распределение

Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов особое положение.

СВ Х распределена по нормальному закону с параметрами , если ее плотность распределения имеет вид:

.

Постоянная с определяется из условия нормировки f(x)   (2-го свойства f(x) ).

Найдем ?

.

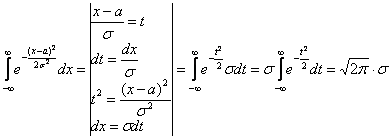- известный интеграл Эйлера-Пуассона.

Специальная функция, называемая функцией распределения Лапласа или «интегралом вероятностей», имеет вид:

.

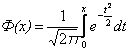Для нее составлены таблицы значений и известно, что

.

Следовательно, имеем

Тогда,  и .

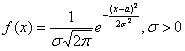Смысл параметров будет установлен позже.

Найдем функцию распределения F(x) для нормального закона распределения.

.

Кривая нормального распределения имеет симметричный колоколообразный (холмообразный) вид. Она симметрична относительно прямой х=а и достигает максимума при х=а, имеет две точки перегиба при . При f(x) асимптотически приближается к оси Ох. При увеличении  кривая становится более пологой.

Рисунок 5.16

      

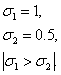
- разброс СВ Х. Чем больше , тем больше разброс.

Найдем вероятность попадания СВ Х в интервал .

Интеграл 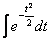 не выражается через элементарные функции, но его можно выразить через интеграл Лапласа.

Замечание.

Следует обратить внимание на пределы функции

.

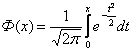Иногда имеются таблицы значений не , а .

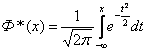Функции  и  связаны между собой соотношением

С помощью функции  вероятность попадания нормально распределенной СВ Х на участок от α до β можно найти по формуле:

.      (10)

Свойства функции Ф(х):

1) Ф(0) = 0;

2) Ф(-х) = - Ф(х) - нечетная функция;

3) Ф(+∞) = 0,5 (при х 5 можно считать, что Ф(х) = 0,5);

4) Ф(-∞) = - 0,5

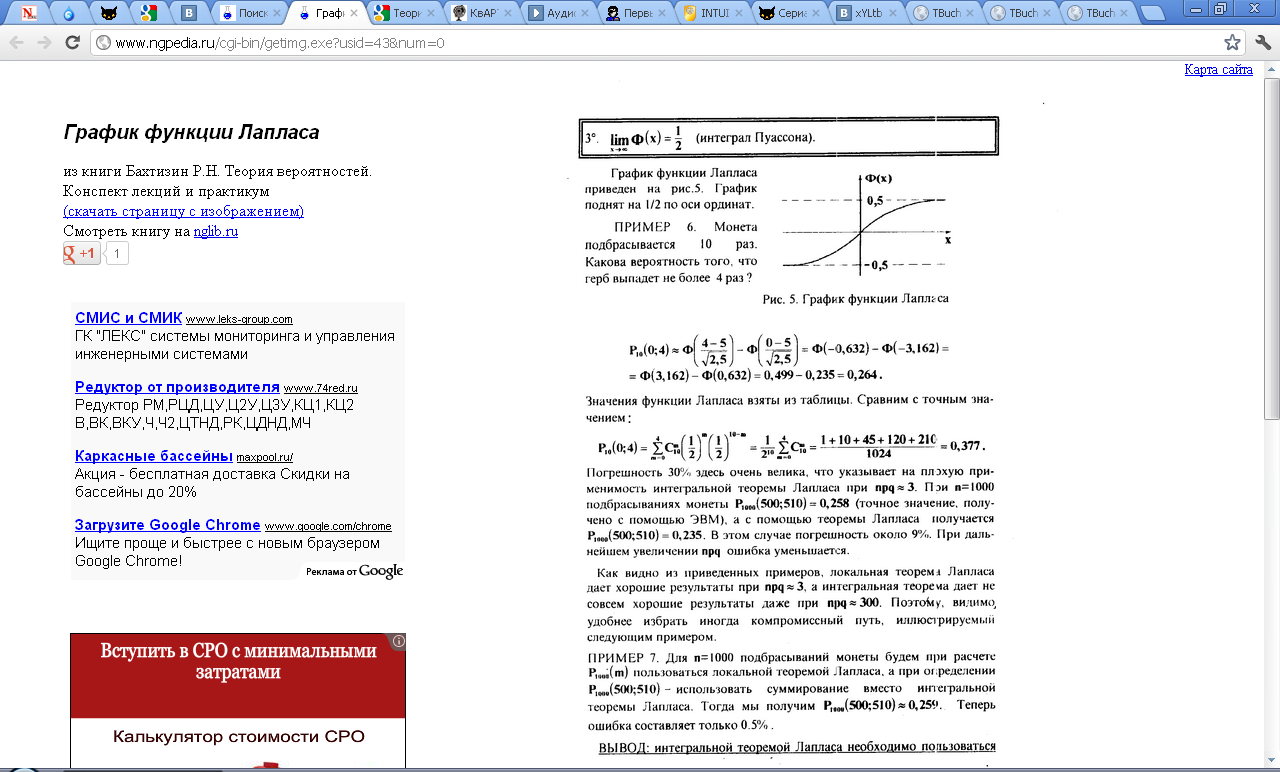
Свойства функции Ф*(х):

1) Ф*(0) = 0,5;

2) Ф*(-х) = 1 – Ф*(х) - нечетная функция;

3) Ф*(+∞) = 1;

4) Ф*(-∞) = 0.

Наиболее просто выражаются через функцию Лапласа вероятность попадания нормально распределенной СВ Х на участок длиной 2l, симметричный относительно центра рассеивания а.

 

Рисунок 5.18

 

.      (11)

При использовании  имеем:

.          (12)

Через функцию Лапласа выражается и функция распределения F(x)  нормально распределенной СВ Х.

По формуле (9), полагая  и учитывая, что , получим:

.                   (12)

Нормальное распределение возникает тогда, когда величина Х образуется в результате суммирования большого числа независимых (или слабозависимых) случайных слагаемых, сравнимых по своему влиянию на рассеивание суммы. Нормальное распределение имеет важное значение для практики. Распределение многих важных практических СВ оказывается подчиненным нормальному закону (рассеивание снарядов при стрельбе в цель и т.д.). Далее увидим, что «универсальность» этого закона объясняется тем, что СВ, равная сумме большого числа независимых СВ оказывается распределенной почти по нормальному закону.

Кроме рассмотренных распределений непрерывных случайных величин существую и другие, важные для практики распределения:

-       Распределение Вейбулла,

-       Гамма-распределение,

-       Распределение Эрланга,

-       Распределение хи-квадрат.

Считают, что распределению Вейбулла подчиняются времена безотказной работы многих технических устройств. При определенных значениях одного из параметров этого распределения оно превращается в экспоненциальное распределение или в распределение Релея.

Гамма-распределение также достаточно хорошо описывает времена безотказной работы различных технических устройств. Распределение Вейбулла и гамма-распределение весьма близки между собой. Основным преимуществом закона Вейбулла перед гамма-распределением является то, что его функция распределения является элементарной функцией.

Распределение Эрланга находит важные применения в теории массового обслуживания.

Роль распределения хи-квадрат в математической статистике невозможно переоценить. Так, например, при проверке статистических гипотез о законе распределения используются критерии согласия. Существует несколько критериев согласия:

-       Критерий Хи-квадрат (критерий Пирсона),

-       Критерий Колмогорова,

-       Критерий Смирнова,

-       Др.

Критерий Пирсона широко применяется для проверки гипотезы о нормальном распределении генеральной совокупности, применяется также и для других распределений. В этом состоит его достоинство.

3. Математическое ожидание и дисперсия классических распределений.

 

Найдем значения математического ожидания и дисперсии для некоторых законов распределения.

3.1.Биномиальное распределение.

Известно, что биномиальное распределение описывается формулой:

,

а математическое ожидание для дискретных случайных величин рассчитывается по формуле:

.

Тогда имеем

Следовательно, M[x]=np – с точностью до целого совпадает с модой (наивероятнейшим значением).

Аналогично можно рассчитать дисперсию:

D_x=npq.

 

3. 2. Распределение Пуассона.

,

(m=0,1,2,….).

Найдем математическое ожидание.

 

=ae^-a =a

 

Таким образом, M[x]=a

Найдем дисперсию. Для дискретных случайных величин: ,

.

(m-a)²=m² - 2ma + a² = (m² – m) – (2ma - m) +a ² = m(m – 1) – m (2a + 1) +a²

Тогда получаем:

D_x = =

= =

⁼

=

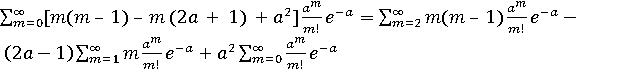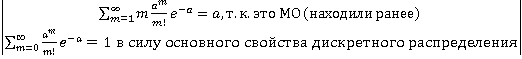Таким образом, для закона Пуассона M[X]= D[X]= a = параметру закона.

 

3. 3. Распределение равномерной плотности

.

.

,

.

 

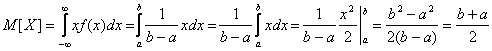3. 4. Показательное распределение

.

.

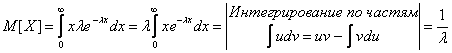Замечание.

Учитывая, что при    быстрее, чем возрастает степень х.

 

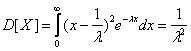
3.5. Нормальное распределение

 

.

 

 

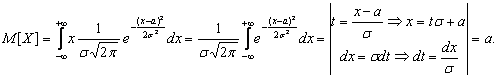
Найдем дисперсию нормального закона распределения.

.

.

Таким образом, дисперсия СВ Х, распределенной по нормальному закону с параметрами  равна , а . Значит , параметр  есть не что иное как С.К.О СВ Х.

 

Величина m_x СВ Х, подчиненной нормальному закону распределения, называется ее центром рассеивания.

Размерности как МО так и С.К.О. совпадают с размерностью СВ Х.

Посмотрим, как будет меняться кривая распределения при изменении параметров .

При изменении а кривая f(x), не изменяя своей формы просто будет смещаться вдоль оси абсцисс.

Изменение  равносильно изменению масштаба кривой по обеим осям: например, при удвоении  масштаб по оси абсцисс удвоится, а по оси ординат – уменьшится в 2 раза.

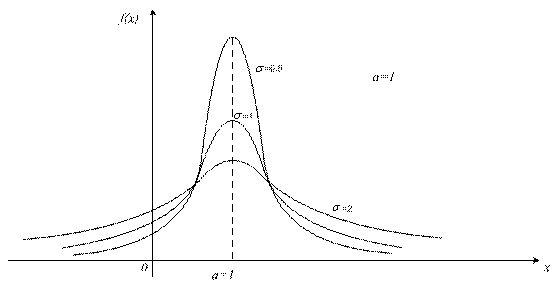
Рисунок 6.4

 

 

Оценим для нормальной СВ Х вероятность попадания на участок от  до , где =а-к и =а+, т.е вероятность попадания в интервал а симметричный относительно m_x=a.

Выше были получены формулы:

 - вероятность попадания нормально распределенной СВ Х на интервал от  до ;

 или  - это вероятность попадания СВ Х на участок длиной 2l, симметричный относительно центра рассеивания а.

В данном случае .

Пусть k=1, тогда:

;

k=2,

;

k=3,

,

т.е. всего с вероятностью 0,0027 случайная величина, распределенная по нормальному закону, попадает за пределы интервала .

 

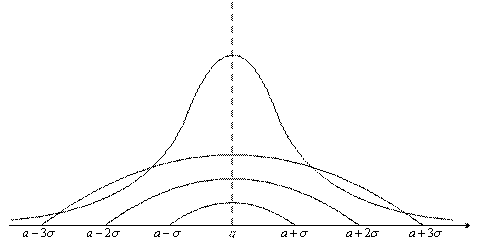
Рисунок 6.5

 

С большой точностью Х попадет внутрь этого интервала. Это правило называется правилом «трех σ» для нахождения интервала рассеивания.

Зная этот интервал возможного рассеивания случайной величины Х ( ) вокруг m_x=a, можно найти .

Для неотрицательной СВ Х в качестве характеристики ее «случайности» иногда применяется коэффициент вариации .