Оглавление

1. Примеры законов распределения дискретных случайных величин 2

1. 1. Биномиальное распределение (биномиальный закон распределения) 2

1. 2.  Распределение Пуассона 2

1.3. Геометрическое распределение 5

1.4. Гипергеометрическое распределение 6

2. Некоторые важные для практики распределения непрерывных случайных величин. 6

2.1. Равномерное распределение (закон равномерного распределения – закон равномерной плотности). 6

2.1.1. Примеры равномерного распределения 8

2.2. Показательное распределение 9

2.3. Нормальное распределение 10

3. Математическое ожидание и дисперсия классических распределений. 15

3.1.Биномиальное распределение. 15

3. 2. Распределение Пуассона. 16

3. 3. Распределение равномерной плотности 17

3. 4. Показательное распределение 17

3.5. Нормальное распределение 17

4. Теоремы о математическом ожидании и дисперсии. 20

5. Моменты. 24

6. Многомерные функции распределения. 29

7. Моменты двумерного случайного вектора. Коэффициент корреляции 34

8. Предельные теоремы теории вероятностей. 38

8.1. Закон больших чисел  38

8.1.1.Сходимость по вероятности. 39

8.1.2. Неравенство Чебышева 40

8.2 Теоремы Чебышева 40

8.3. Закон больших чисел для разных условий опыта (теорема Маркова) 42

8.4. Примеры использования закона больших чисел при решении задач 44

8.5. Центральные предельные теоремы 45

1. Примеры законов распределения дискретных случайных величин

 

Рассмотрим некоторые важные для практики распределения дискретных  случайных величин.

1. 1. Биномиальное распределение (биномиальный закон распределения)

Говорят, что ДСВ имеет биномиальное распределение, если ее возможные значения: 0, 1, 2, …, m,…..n, а соответствующие им вероятности выражаются формулой:

P(m) =P{X=m} = C^m_n  p^m q^n-m , где m=0, 1, 2, ….. n, (3)

0<p<1, q= 1-p

или, что то же самое, рядом распределения, представленным в таблице 1.

 

Таблица 1

X=m	0	1	…	i	…	n
			…		…

 

Формула (3) – формула Бернулли, является аналитическим выражением биномиального закона распределения. Таким образом, биномиальным называют распределение вероятностей, определяемое формулой Бернулли. 

Распределение зависит от двух параметров: n и p

На практике биномиальное распределение возникает при следующих условиях. Пусть производится n  независимых опытов (независимые опыты – опыты, при которых вероятность какого-либо исхода каждого из них не зависит от того, какие исходы имели другие опыты), в каждом из которых событие А (условно его можно назвать «успехом» опыта) появляется с вероятностью р.

Следовательно, биномиальное распределение является ни чем иным, как распределением числа успехов Х вn испытаниях по схеме Бернулли с вероятностью успеха p и неудачи q=1-p.

СВ Х – это число «успехов» при n опытах.

 

1. 2. Распределение Пуассона

Говорят, что случайная величина Х  имеет распределение Пуассона, если ее возможные значения: 0, 1, 2, …,m,… (бесконечное, но счетное множество значений), а соответствующие вероятности выражаются формулой:

    (4)

m= 0, 1, 2, ….

Это распределение – предельное для биномиального распределения при n  и р0 и при условии, чтоnр=a=const. Закон Пуассона зависит от одного параметра а, смысл которого в следующем: он является одновременно МО и дисперсией СВ Х, распределенной по закону Пуассона.

Ряд распределения представлен в таблице 2

 

Таблица 2

X=m	0	1	2	…	m	…	
							0

 

Имеются специальные таблицы, пользуясь которыми можно найти P_m, зная m  и а.

При а =1 имеем ряд распределения, представленный в таблице 3

 

Таблица 3

X=m	0	1	2	3	4
	0.36788	0.36788	0.18394	0.06131	0.01533

 

Графическое изображение этого ряда распределения имеет вид, представленный на рисунке 10.

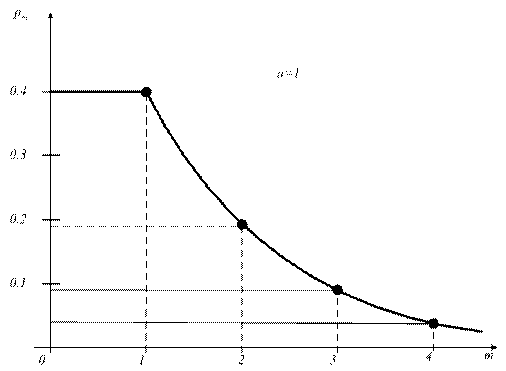
Рисунок 5.10

 

Распределение Пуассона играет большую роль в практическом применении теории вероятностей: многие физические явления приводят именно к такому распределению вероятностей.

Распределение Пуассона является распределением класса редких случайных событий (явлений), то есть таких событий, когда появление двух и более событий за малый промежуток времени практически невозможно.

Это распределение называют также законом редких событий, так как оно всегда проявляется там, где производится большое число испытаний, в каждом из которых с малой вероятностью происходит «редкое» событие. В соответствии с законом Пуассона распределены, например, число метеоритов, упавших в определенном районе; число распавшихся частиц при радиоактивном распаде вещества; число вызовов, поступивших в течение суток на телефонную станцию.

Пусть – среднее число событий, которые появляются в единицу времени  

Какова вероятность того, что за время  произойдет ровно m событий, т.е.

 

P(m, )-?

 

Интервал времени  всегда можно разбить на такие одинаковые промежутки , что в каждом из них будет происходить не более одного события. Тогда число интервалов

.

Вероятность того, что событие произойдет в одном из интервалов , равна

 - вероятность появления   благоприятных событий

 

Откуда n_p= =a

 

При n , p 0,  =const. Найдем искомую вероятность

 

 .

Это вероятность того, что за время  произойдет ровно m событий определенных формулой. Имеются специальные таблицы, по которым, зная m и  , можно найти вероятность P(m,  ). λ  - называют интенсивностью.

Пример.

На входе ВС появляется задание на обслуживание с интенсивностью 120 зад/мин. Найти вероятность событий:

А={ за 1 сек. не приходит ни одного задания}

В = {за 1 сек. приходит хотя бы одно задание}

С = {за 1 сек. приходит ровно 1 задание}

λ = 120 зад/сек = = 2 зад/с

Р(А) - ?

m = 0; τ = 1.

λτ = 2

Р(А) = Р (0, 2) = = 0,13534

Р(В) = 1 – P(A) - событие, противоположное событию А.

Р(В) = 1 – 0, 13534 = 0,86466

Р(С) = Р(1,2) =   =0, 27067