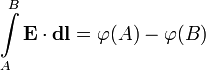- •6 (Силы внеш, внут. Связь з-на сохран со св-ми простр и врем)
- •9 (Кин.Энерг, закон сохр полн мех энерг)
- •1 1(Момент импульса частицы)
- •12(Момент инерции тв.Тела, ур.Динам.Вращ.)
- •13 (Кинем.Эн.Вращ.Тв.Тела /ось закр/, раб.Внеш.Сил)
- •21Гармонические колебания.
- •29 (Распрост.Волн в упругой среде)
- •31(Энергия продольной одномерной волны)
- •32 (Поток и плотн.Потока энергии упр.Волны. Вектор Умова)
- •33(Макроскопическая системма……)
- •34(Фазовое пространство скоростей)
- •35 Характерные скорости
- •36 Функция рапределения больцмана
- •39 (Закон сохранение заряда. Напряжённость поля)
- •41 (Поток е. Теорема Гаусса)
- •42 (Пример расчёта поля беск. Заряж. Нити)
- •43 (Пример расчета поля бескон.Заряж.Плоскости)
- •44 (Дифференц. Форма теоремы Гаусса)
- •45 (Теорема циркуляции е. Потенциал)
- •46 (Эл.Диполь, момент милы действ.На диполь, эн. Диполя)
- •47 (Поляризация диэл. Вектор поляризации)
- •48 (Вектор d и теорема Гаусса)
- •50 (Энергия эл.Поля)
- •51 (Сигнетоэлектрики. Электр. Гистерезис)
- •63 (Магнитное поле в веществе)
- •64 (Вектор н)
- •66 (Ферромагнетики. Гистерезис)
- •68 (Явл.Самоиндукции, индуктивность)
- •69. Ток смеще́ния Энергию магнитного
- •72 Свободные колебания в контуре без активног сопротивления
- •73. Свободные и затухающие колебания в контуре.
- •74(Вынужденные электрические колебания)
35 Характерные скорости
хотя Уравнение (11) дает распределение скоростей, или, другими словами, долю молекул, имеющих специфическую скорость, часто более интересны другие величины, такие как средние скорости частиц. В следующих подразделах мы определим и получим наиболее вероятную скорость, среднюю скорость и среднеквадратичную скорость.
Наиболее вероятная скорость
наиболее
вероятная скорость, ![]() —
вероятность обладания которой любой
молекулой системы максимальна, и которая
соответствует максимальному значению
—
вероятность обладания которой любой
молекулой системы максимальна, и которая
соответствует максимальному значению ![]() .
Чтобы найти её, необходимо вычислить
.
Чтобы найти её, необходимо вычислить ![]() ,
приравнять её нулю и решить относительно
,
приравнять её нулю и решить относительно ![]() :
:
![]()
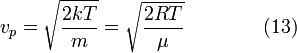
36 Функция рапределения больцмана
37


38


39 (Закон сохранение заряда. Напряжённость поля)
Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме:

Здесь
![]() —
некоторая произвольная область в
трёхмерном пространстве,
—
некоторая произвольная область в
трёхмерном пространстве,
![]() —
граница этой области,
—
граница этой области,
![]() —
плотность заряда,
—
плотность заряда,
![]() —
плотность тока (плотность потока
электрического заряда) через
границу.Напряжённость
электри́ческого по́ля —
векторная физическая величина,
характеризующая электрическое поле в
данной точке и численно равная отношению
силы
—
плотность тока (плотность потока
электрического заряда) через
границу.Напряжённость
электри́ческого по́ля —
векторная физическая величина,
характеризующая электрическое поле в
данной точке и численно равная отношению
силы
![]() действующей
на неподвижный пробный заряд, помещенный
в данную точку поля, к величине этого
заряда
действующей
на неподвижный пробный заряд, помещенный
в данную точку поля, к величине этого
заряда
![]() :
:
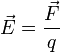 .Напряжённость
электрического поля в СИ измеряется в
вольтах на метр [В/м] или в ньютонах на
кулон.
.Напряжённость
электрического поля в СИ измеряется в
вольтах на метр [В/м] или в ньютонах на
кулон.
41 (Поток е. Теорема Гаусса)

 – поток
Е.
– поток
Е.
Т.Гаусса:
поток вект.Е через .произвол.замкн.поверх.
=алгебр.сумме зарядов внутри этой пов.,
делен. на ε0.
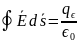
Интегр.по замкн.пов.=∑интегр.по элементам откр.поверхности.
Поток зависит только от зарядов, оказавш.внутри.
П оверхность
произвольной формы. Пров. при заряде
внутри:
оверхность
произвольной формы. Пров. при заряде
внутри:




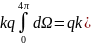
42 (Пример расчёта поля беск. Заряж. Нити)
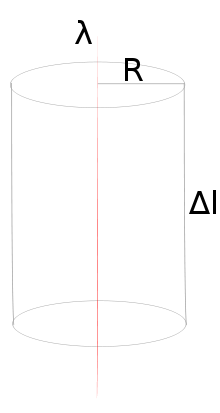
Расчёт напряжённости поля бесконечной нити
![]()
Рассмотрим
поле, создаваемое бесконечной прямолинейной
нитью с линейной плотностью заряда,
равной
![]() .
Пусть требуется определить напряжённость,
создаваемую этим полем на расстоянии
.
Пусть требуется определить напряжённость,
создаваемую этим полем на расстоянии
![]() от нити. Возьмём в качестве гауссовой
поверхности цилиндр с осью, совпадающей
с нитью, радиусом
и
высотой
от нити. Возьмём в качестве гауссовой
поверхности цилиндр с осью, совпадающей
с нитью, радиусом
и
высотой
![]() .
Тогда поток напряжённости через эту
поверхность по теореме Гаусса таков (в
единицах СИ):
.
Тогда поток напряжённости через эту
поверхность по теореме Гаусса таков (в
единицах СИ):

Тогда поток напряжённости через эту поверхность можно рассчитать следующим образом:
![]()
Учитывается
только площадь боковой поверхности
цилиндра, так как поток через основания
цилиндра равен нулю (вследствие
направления E
по касательной к ним). Приравнивая два
полученных выражения для
![]() ,
имеем:
,
имеем:
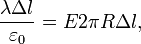
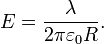
43 (Пример расчета поля бескон.Заряж.Плоскости)
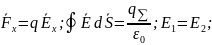

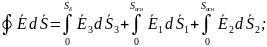

 Е1
– пост.велич на верх. Площадке основ.,не
завис.от dS;
Е1
– пост.велич на верх. Площадке основ.,не
завис.от dS;

44 (Дифференц. Форма теоремы Гаусса)
Пусть эл.заряд распред.в 3х-мерном простр. нек. потностью.
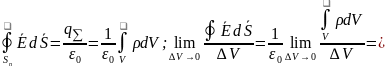

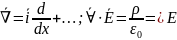 (отношение)
(отношение)
Скалярн.производн.E – пред.отнош.поток.Е к изм.объем.
45 (Теорема циркуляции е. Потенциал)
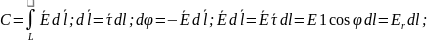
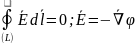 (градиент)
(градиент)
Электростатический потенциа́л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля.
Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:
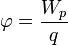
Напряжённость
электростатического поля
![]() и потенциал
и потенциал
![]() связаны
соотношением
связаны
соотношением