17. Подшипники скольжения

Подшипники, работающие по принципу трения скольжения, называются подшипниками скольжения.

Простейшим подшипником скольжения является отверстие, расточенное непосредственно в корпусе машины, в которое обычно вставляют втулку (вкладыш) из антифрикционного материала рис. 13.1.

Р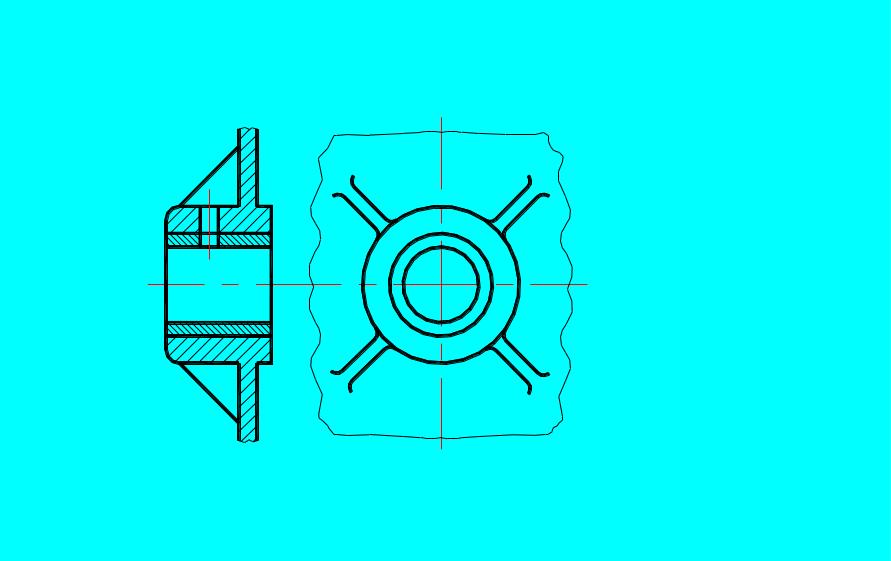 ис. 13.1. Подшипник скольжения

13.1.2. Разновидности подшипников скольжения

По характеру воспринимаемой нагрузки подшипники подразделяются на следующие виды:

Радиальные, воспринимающие только радиальную нагрузку.

Радиально–упорные, воспринимающие радиальную и осевую нагрузки.

Упорные, воспринимающие только осевую нагрузку.

По форме рабочей поверхности (рис. 13.2) – с цилиндрической (а), конической (б), сферической (в) и плоской (г) рабочей поверхностью.

Достоинства подшипников скольжения:

надежно работают в высокоскоростных приводах;

способны воспринимать большие ударные и вибрационные нагрузки вследствие демпфирующего действия масляного слоя;

обеспечивают высокую точность установки вала;

работают бесшумно;

имеют малые габариты в радиальном направлении;

разъемные подшипники допускают установку их на шейки коленчатых валов;

возможность использования при работе в агрессивной среде.

Недостатки подшипников скольжения:

в процессе работы требуют постоянного надзора из-за высоких требований к смазке и опасности перегрева;

большие габариты в осевом направлении;

большой расход смазочного материала;

необходимость применения дорогостоящих и дефицитных антифрикционных материалов для вкладышей

Расчет подшипников с полужидкостным и граничным трением

Это подшипники тихоходных машин с частыми пусками и остановками, плохими условиями смазки.

Расчет проводят по двум показателям:

Среднему давлению между цапфой и вкладышем:

Р = F_r/(dl)  [P],

где F_r – радиальная нагрузка на подшипник; d и l – диаметр и длина цапфы; [P] – допускаемое давление, которое определяется в зависимости от материала вала и вкладыша.

Расчет по Р гарантирует невыдавливание смазки и представляет собой расчет на износостойкость.

По произведению [PV]:

где V– окружная скорость цапфы. [PV] определяется в зависимости от материалов вала и вкладыша и характеризует удельную работу сил трения. Расчет по [PV] гарантирует нормальный тепловой режим и стойкость против заедания.

Подпятники скольжения рассчитываются по аналогичной методике, но ввиду худших условий отвода теплоты допускаемые значения [P] и [PV] уменьшаются на 20 - 30%.

18. Проверка червяка

В червячной паре менее прочным элементом является зуб червячного колеса, для которого возможны следующие виды разрушений: 1) усталостное контактное выкрашивание; 2) износ; 3) заедание и 4) поломка зубьев.

В отличие от зубчатых, в червячных передачах износ и заедание наблюдаются чаще, чем выкрашивание и поломка, что связано со значительным скольжением. Следовательно, износостойкость и стойкость против заедания – основные критерии работоспособности червячных передач. Дополнительные критерии работоспособности – изгибная прочность зубьев колеса и жесткость червяка.

Для уменьшения износа и предупреждения заедания необходимо ограничивать величину контактных напряжений. Поэтому для червячной передачи проектным является расчет по контактным напряжениям. В качестве проверочного проводится расчет зубьев колеса по контактным напряжениям и напряжениям изгиба, а червяка – на жесткость.

Формула для проверочного расчета зубьев колеса на контактную выносливость

где σ_H – действительное контактное напряжение; σ_HР – допускаемое контактное напряжение для материала зуба червячного колеса; K_H – коэффициент нагрузки, который учитывает неравномерность распределения нагрузки вследствие деформации деталей передачи и дополнительные динамические нагрузки.

Формула для проектного расчета зубьев колеса на контактную выносливость

Формула для проверочного расчета зубьев колеса на выносливость при изгибе

где Y_F – коэффициент формы зуба (определяют в зависимости от эквивалентного числа зубьев z_v = z/cos³γ); F_t2 – окружная сила на колесе; b₂ – ширина зубчатого венца колеса; m_n = m·cosγ – нормальный модуль.

Кроме того, необходимо выполнять проверочный расчет червяка на жесткость. Для обеспечения нормальной работы прогиб червяка не должен превышать допускаемый f ≤ [f], f = (0.005 – 0.01)m. Стрела прогиба f находится по формулам сопротивления материалов.