29. Теплопередача через оребр стенку
Стенка оребрена со стороны меньшего коэффициента теплоотдачи Заданы постоянные значения коэффициентов теплоотдачи на неоребренной поверхности стенки 1, гладкой части оребренной поверхности с и на поверхности ребер р. Заданы геометрические размеры ребер и температуры теплоносителей tF1 и tF2.
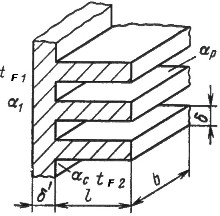
Рис. 2.14. Теплопередача через ребристую стенку.
Поскольку для ребра Ь>>δ, то полагаем, что периметр поперечного сечения ребер u=2Ь. Площадь поперечного сечения ребра f=Ьδ.
Подставив выражение
для m в уравнение (2.85), умножив и разделив
на 2l, получим предыдущее выражение, где
рδ/λ=Bi - безразмерный комплекс, называемый
числом Био. Число Bi является важной
характеристикой процесса теплопроводности.
Оно представляет собой отношение
внутреннего термического сопротивления
теплопроводности к внешнему термическому
сопротивлению теплоотдачи:
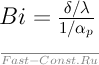
Окончательное уравнение для теплового потока с поверхности ребра можно записать в виде
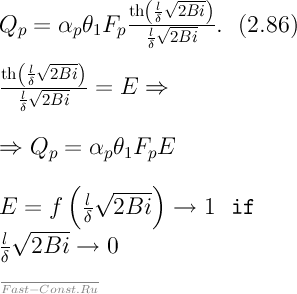
(при заданных геометрических размерах ребра последнее возможно, если λ стремиться к бесконечности, т. е. Biстремиться к нулю). Величина Е называется коэффициентом эффективности ребра. Тепловой поток Qc,Вт, отдаваемый гладкой частью оребренной поверхности,
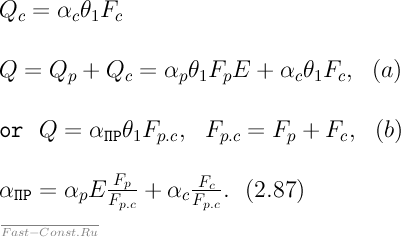
(а) - уравнение общего теплового потока. Из сопоставления (а) и (б) следует (2.87). Величина пр, входящая в уравнение (2.87), называется приведенным коэффициентом теплоотдачи. Это такой усредненный коэффициент теплоотдачи ребристой стенки, который учитывает теплоотдачу поверхности ребра, поверхности гладкой стенки и эффективность работы ребра.
Для передачи теплоты через ребристую стенку можно записать систему уравнений:
Из этих уравнений получаем
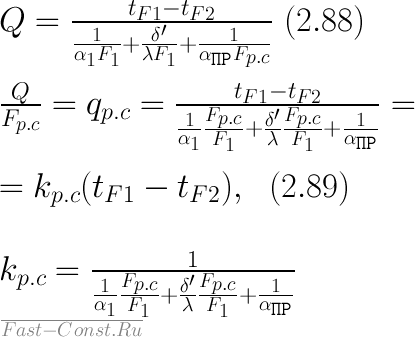
Если тепловой поток отнести к единице оребренной поверхности стенки, то получаем (2.89), где kp.c - коэффициент теплопередачи через ребристую стенку при отнесении тепловогб потока к оребренной поверхности, Вт/(м2К).
Если тепловой поток отнести к неоребренной поверхности стенки, то получим:
k1— коэффициент теплопередачи при отнесении теплового потока к неоребренной поверхности стенки.
Отношение оребренной поверхности Fp.c к гладкой F1 называется коэффициентом оребрения.
Влияние оребрения на коэффициент теплопередачи можно показать на следующем примере. Пусть 1=1000 и 2=20Вт/(м2К). Предположим, что δ'/λ мало и им можно пренебречь, тогда
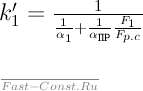
Для плоской поверхности (коэффициент оребрения Fp.c/F1 равен единице) получим:
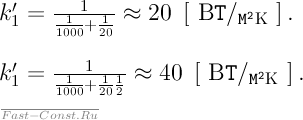
Последнее выражение, если стенка имеет ребра с одной стороны, причем коэффициент Fp.c/F1=2. Следовательно, при заданных соотношениях коэффициентов теплоотдачи при оребрении плоской стенки со стороны малого с коэффициентом оребрения Fp.c/F1=2 передача теплоты увеличивается примерно в 2 раза.
30. Конвективный теплообмен. Закон Ньютона-Рихмана
Конвективным теплообменом называется одновременный перенос теплоты конвекцией и теплопроводностью. В инженерных расчетах часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей. Основными факторами, влияющими на процесс теплоотдачи являются следующие: 1). Природа возникновения движения жидкости вдоль поверхности стенки. Самопроизвольное движение жидкости (газа) в поле тяжести, обусловленное разностью плотностей её горячих и холодных слоев, называют свободным движением (естественная конвекция). Движение, создаваемое вследствие разности давлений, которые создаются насосом, вентилятором и другими устройствами, называется вынужденным (вынужденная конвекция). 2). Режим движения жидкости. Упорядоченное, слоистое, спокойное, без пульсаций движение называется ламинарным. Беспорядочное, хаотическое, вихревое движение называется турбулентным. 3). Физические свойства жидкостей и газов. Большое влияние на конвективный теплообмен оказывают следующие физические параметры: коэффициент теплопроводности (), удельная теплоемкость (с), плотность (ρ), κкоэффициент температуропроводности (а = λ/cр·ρ), коэффициент динамической вязкости (μ) или кинематической вязкости (ν = μ/ρ), тεмпературный коэффициент объемного расширения (β = 1/Т). 4). Форма (плоская, цилиндрическая), размеры и положение поверхности (горизонтальная, вертикальная).